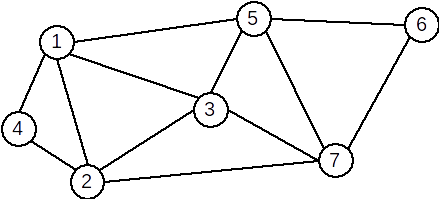Clasa a XI-a lecția 19

Graf eulerian

Definiție: Se numește graf eulerian un graf care conține un ciclu eulerian. Se numește ciclu eulerian un ciclu care conține toate muchiile grafului.

Exemplu: Graful următor este eulerian. Un ciclu eulerian este: [1,4,2,1,3,2,7,3,5,7,6,5,1] [1,4,2,1,3,2,7,3,5,7,6,5,1]

Teoremă: Un graf G = (X,U), fără vârfuri izolate, este eulerian dacă şi numai dacă este conex şi gradele tuturor vârfurilor sale sunt numere pare.

Euler

Se dă un graf neorientat cu n vârfuri care este conex și are gradele tuturor vârfurilor pare. Determinați un ciclu eulerian.

#include <fstream>

using namespace std;
ifstream in ("euler.in");
ofstream out("euler.out");

int n, a[1001][1001], v[1001], p;

void euler( int k ){
  for( int i = 1; i <= n; i ++ )        // parcurgem toate muchiile neselectate ce pornesc din nodul k
    if( a[k][i] == 1 ){
	  a[k][i] = a[i][k] = 0;            // marcam ca muchia ca si selectat
	  euler( i );                       
	}
	v[++p] = k;                         // salvam ordinea de vizitare a nodurilor
}

int main(){
  int i, j;
  in >> n;
  while( in >> i >> j )
    a[i][j] = a[j][i] = 1;
  euler( 1 );
  out << p << "\n";
  for(i = 1; i <= p; i++ )
    out << v[i] << " ";
  return 0;
}

Tema

usor

• https://www.pbinfo.ro/?pagina=probleme&id=545 Realizati implementarea proprie
• https://www.pbinfo.ro/?pagina=probleme&id=1021

Medie

• https://www.pbinfo.ro/?pagina=probleme&id=1021 cartite OJI 2014, Clasele XI-XII BFS pe matrice + Euler

https://www.infoarena.ro/problema/fotbal2 ONI 2011, clasele 11-12 https://www.infoarena.ro/problema/biti