Clasa a 7-a Lecția 5: Precalculare

Înregistrare video lecție

Despre precalculare

Precalcularea este un termen general pentru folosirea unor structuri auxiliare de date, uneori fără o legătură directă cu problema de rezolvat, care ne ajută în rezolvarea problemei.

Aceste structuri de date sunt calculate la început, înainte de calculul propriu zis, ceea ce duce la denumire: precalculare.

De obicei precalcularea reduce complexitatea anumitor pași din algoritm, prețul ei fiind un calcul mic la început, astfel încât, per total, algoritmul va fi mai rapid.

În engleză acest subiect este numit precomputation. Wikipedia oferă exemple de algoritmi complecși de precalculare. Noi vom discuta în continuare despre algoritmi de precalculare de bază, ce apar uzual în programare și la concursuri.

Santinela în căutarea liniară

Precum știm, codul clasic de căutare a elementului e în vectorul v[] de n elemente este:

i = 0;
while ( i < n && v[i] != e )
  i++;
if ( i < n ) // ... testul daca am gasit elementul

Am discutat cum putem elimina unul din testele din while folosind o santinelă. Vom așeza e pe prima poziție în afara vectorului. Astfel, ne asigurăm că vom găsi elementul în vector. Putem, deci, să nu mai testăm condiția i. Noul cod va fi:

v[n] = e;
i = 0;
while ( v[i] != e )
  i++;
if ( i < n ) // ... testul daca am gasit elementul

Așezarea santinelei în vector poate fi un exemplu foarte simplu de precalculare. Ea va folosi un element al vectorului, ce va trebui dimensionat cu unu în plus.

Avantaje: cod mai rapid și mai scurt.
Schimbă complexitatea algoritmului: nu.
Timp precalculare: O(1).
Memorie extra folosită: O(1) (un element în plus).

Bordarea

Bordarea, tehnica prin care înconjurăm matricea cu elemente distincte, ar putea fi și ea considerată o precalculare. În loc de o santinelă avem acum multiple santinele. Codul de testare al depășirii matricei se simplifică și devine mai eficient.

Avantaje: cod mai rapid și mai scurt.
Schimbă complexitatea algoritmului: nu.
Memorie extra folosită: O(n) (n este dimensiunea matricei).

Precalculare de tip caracter

Dacă avem nevoie să aflăm dacă un caracter dat este cifră, testul clasic este:

if ( ch >= '0' && ch <= '9' )
  // ...

Putem elimina un test dacă precalculăm un vector de stegulețe, pentru toate caracterele, care să aibă 1 pe pozițiile caracterelor cifre și 0 în rest. Astfel:

char ecifra[128];

// precalculare: initializare ecifra[]
for ( ch = '0'; ch <= '9'; ch++ )
  ecifra[ch] = 1;

// test cifra
if ( ecifra[ch] )
  // ...

Vom calcula la început câte o valoare per cifră. Apoi, în algoritm vom scuti unul din teste.

Din fericire nu trebuie să facem explicit acest lucru. Biblioteca ne oferă funcția:

int isdigit( int ch )

Aceasta face exact ce ne dorim.

Există și alte funcții, cum ar fi isalpha() (testare literă) și isalnum() (testare cifra sau litera).

Avantaje: cod mai rapid și mai scurt.
Schimbă complexitatea algoritmului: nu.
Timp precalculare: O(Σ) (unde Σ este numărul de caractere).
Memorie extra folosită: O(Σ) (unde Σ este numărul de caractere).

Prelucrare valori cifre în baze de numerație

Să luăm ca exemplu problema criptic. La intrare se aflau numere în baza 62, ce trebuiau citite ca întregi în memorie. Pentru aceasta trebuia să calculăm valoarea unei cifre. Codul simplu și direct va fi:

char ch;
// ...
ch = fgetc( fin );
if ( ch >= '0' && ch <= '9' )
  v = ch - '0';
else if ( ch >= 'a' && ch <= 'z' )
  v = ch - 'a' + 10;
else
  v = ch - 'A' + 36;

El va face 2 sau 4 teste de inegalitate. Pentru a nu avea nici un test putem precalcula într-un vector valorile cifrelor în baza 62:

int val[128];
// ...
for ( ch = '0'; ch <= '9'; ch++ ) // valorile cifrelor
  val[ch] = ch - '0';
for ( ch = 'a'; ch <= 'z'; ch++ )
  val[ch] = ch - 'a' + 10;
for ( ch = 'A'; ch <= 'Z'; ch++ )
  val[ch] = ch - 'A' + 36;

Apoi, la folosire:

char ch;
// ...
ch = fgetc( fin );
v = val[ch];

Avantaje: cod mai rapid și mai scurt.
Schimbă complexitatea algoritmului: nu.
Timp precalculare: O(Σ) (unde Σ este numărul de caractere).
Memorie extra folosită: O(Σ) (unde Σ este numărul de caractere).

Ciurul lui Eratostene

V-aţi gândit vreodată că ciurul lui Eratostene este de fapt o precalculare a unui vector de frecvenţă ciur[], care, pentru fiecare număr p, calculează ciur[p] care ne spune dacă p este prim?

Cum am calcula primalitatea tuturor numerelor până la n în absența ciurului? Am verifica de primalitate fiecare din numere, în O(p). Complexitatea algoritmului ar fi: ${\sqrt {1}}+{\sqrt {2}}+{\sqrt {3}}+...+{\sqrt {n}}$ .

Această sumă este $O(n{\sqrt {n}})$ (demonstrația depășește nivelul cercului nostru). În realitate lucrurile stau puțin mai bine, în sensul că nu vom ajunge cu divizorii până la ${\sqrt {k}}$ decât pentru k prim. O estimare a numerelor prime până la n este ${\frac {n}{log{n}}}$ .

De aceea, o estimare ajustată a complexității ar fi $O({\frac {n{\sqrt {n}}}{log{n}}})$ .

Am putea face și o altă optimizare: să împărțim k doar la numerele prime de până la el. Aceasta mai reduce complexitatea într-un mod ce ar complica și mai mult formula.

Să nu uităm un lucru important: factorizarea folosește împărțiri. Ceea ce, pentru numerele cu care lucrăm noi, introduce o constantă multiplicativă foarte mare, circa 15 până la 30, comparabilă cu optimizări de tipul O(log n).

Prin comparație, ciurul lui Eratostene general are complexitatea O(n log n) și nu folosește împărțiri, iar pentru cazul testului de primalitate el poate fi adus la O(n log log n).

Să ne reamintim unele din aplicațiile ciurului lui Eratostene:

Numărul de divizori primi (unici sau neunici) ai tuturor numerelor până la n
Suma divizorilor primi (unici sau neunici) ai tuturor numerelor până la n
Numărul de divizori ai tuturor numerelor până la n
Suma divizorilor tuturor numerelor până la n
Descompunerea în factori primi a tuturor numerelor până la n
Numărul de numere prime cu fiecare din numerele până la n

Concluzii:

Avantaje: cod mai rapid și mai scurt.
Schimbă complexitatea algoritmului: da.
Timp precalculare: O(n log n) sau O( n log log n).
Memorie extra folosită: O(n).

Suma între i și j

În multe probleme apare următoarea subproblemă: dat un vector v[] de n elemente întregi, să se răspundă la multe întrebări de forma care este suma elementelor vectorului între poziţiile i şi j?.

În acest caz vom precalcula o structură de date auxiliară, şi anume un vector s[], astfel încât s[i] este suma elementelor de la 0 până la i (inclusiv). El se mai numeşte şi vectorul sumei prefixelor lui v[]. Construcția acestui vector se poate face liniar deoarece avem relaţia s[i] = s[i-1] + v[i].

Odată calculat acest vector putem răspunde în timp constant la întrebări. Suma elementelor între i şi j este s[j] - s[i-1].

Complexitatea algoritmului forță brută de calcul al unei sume ar fi O(n), pe medie. Precalcularea o reduce la O(1).

Avantaje: cod mai rapid și mai scurt.
Schimbă complexitatea algoritmului: da.
Timp precalculare: O(n).
Memorie extra folosită: O(n).

Sumele parțiale pot fi folosite și pentru a răspunde rapid la alt tip de întrebări: dat S, care este cea mai mare poziție i în vector cu proprietatea că suma elementelor de la 0 la i este mai mică sau egală cu S?

Sumele parțiale într-un vector cu elemente naturale au proprietatea că sunt crescătoare. De aceea putem căuta suma S binar în vectorul de sume parțiale. Răspunsul la întrebare ar fi O(n) prin forță brută. Folosind sume parțiale putem răspunde în O(log n).

Suma între (l1, c1) şi (l2, c2)

Este problema anterioară extinsă la matrice: avem o matrice de numere întregi şi întrebări de forma: care este suma elementelor matricei în dreptunghiul care are drept colţuri opuse (l1, c1) şi (l2, c2)?.

În mod similar vom precalcula o matrice auxiliară cu suma elementelor matricei originale între (0, 0) şi (i, j). Ea poate fi calculată în timp constant per element, astfel:

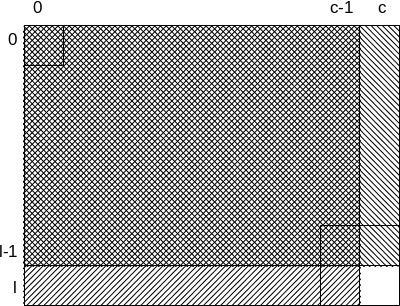
Calcul matrice sume parțiale în dreptunghiuri care pornesc în origine

s[l][c] = s[l][c-1] + s[l-1][c] - s[l-1][c-1] + m[l][c]

s este matricea pe care o precalculăm;
m este matricea cu valorile inițiale.

Odată calculată matricea s[][] putem răspunde în timp constant la întrebări. Suma elementelor între (l1, c1) şi (l2, c2) este:

Calcul suma numerelor în orice dreptunghi

S = s[l2][c2] - s[l2][c1-1] - s[l1-1][c2] + s[l1-1][c1-1]

S este suma căutată;
s este matricea pe care o precalculăm.

Complexitatea algoritmului forță brută de calcul al unei sume ar fi O(n²), pe medie. Precalcularea o reduce la O(1).

Avantaje: cod mai rapid și mai scurt.
Schimbă complexitatea algoritmului: da.
Timp precalculare: O(n²).
Memorie extra folosită: O(n²).

Numărul de biţi 1 într-un întreg

Cum putem calcula numărul de cifre 1 din reprezentarea în baza 2 a unui număr?

Direct: shift and mask. Complexitate O(nr. biţi)
Folosind expresia x & (x - 1). Complexitate O(nr. biţi)
Cu precalculare: ţinem un vector în care elementul v[x] este numărul de biţi 1 din reprezentarea în baza 2 a lui x.

Concluzii precalculare număr de biți 1:

Avantaje: cod mai rapid.
Schimbă complexitatea algoritmului: da.
Timp precalculare: O(xMax log xMax).
Memorie extra folosită: O(2nr. biți), sau O(xMax). Poate fi prohibitiv dacă xMax este mare.

Întrebări:

Se poate mai bine decât O(nr. biţi) fără memorie suplimentară (adică O(1) memorie suplimentară)?
Putem adapta metoda precalculării și la numere xMax mari, gen numere întregi pe int?

Vector de diferențe (difference array)

Mai poartă denumirea și de sume de intervale sau șmenul lui Mars

Se dă un vector cu n elemente, iniţial zero. O operaţiune pe acest vector constă în incrementarea fiecărui element între indicii i şi j. Se dau m operaţiuni de executat. Să se afişeze valorile finale ale vectorului.

Soluţia forţă brută implică execuţia celor m operaţiuni. O operaţiune constă în incrementarea a maxim n elemente din vector, deci avem n x m operaţii, plus afişarea elementelor finale. Complexitatea totală este O(mn).

Exemplu

În următorul exemplu avem un vector inițial zero și se cere să executăm două operațiuni: operațiunea a va incrementa elementele de la pozițiile 2 la 13 și operațiunea b care va incrementa elementele de la pozițiile 6 la 9.

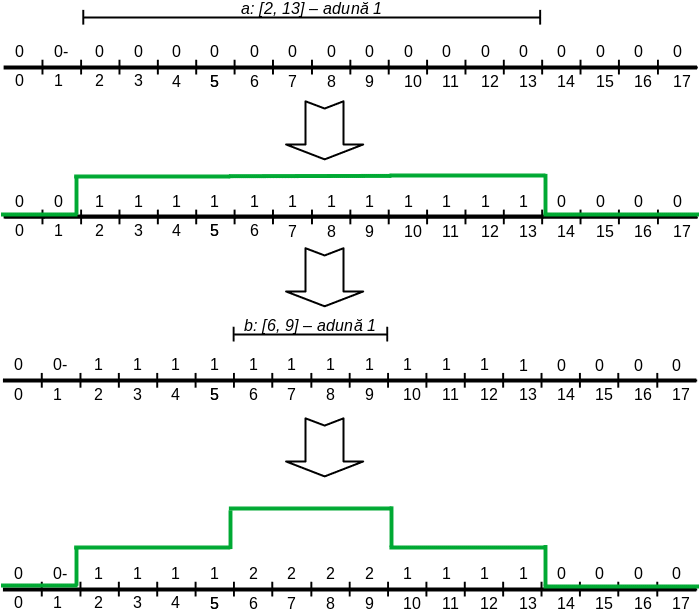
Operațiuni aplicate cu metoda forță brută

Îmbunătățire

Se poate mai bine? Putem optimiza timpul unei operaţiuni. Ideea este următoarea: în loc să incrementăm pe rând elementele vectorului, am putea să le grupăm. Pentru aceasta vom întârzia incrementarea, marcând doar locurile unde trebuie să adunăm.

Cu alte cuvinte: am putea considera intervalele ca pe nişte paranteze aşezate pe o dreaptă. O paranteză deschisă înseamnă că de acum înainte trebuie să adunăm 1 la toate elementele care urmează. O paranteză închisă înseamnă că ne putem opri din adunat 1. Să presupunem că nu avem capete de interval suprapuse. Atunci am putea memora parantezele într-un vector separat. Vom memora 1 pentru o paranteză deschisă, -1 pentru o paranteză închisă şi 0 în caz că nu avem nici un capăt de interval în acel element.

Ipoteză: vectorul s[] de sume parţiale ale acestui vector constituie chiar rezolvarea problemei.

Avem, deci: s[i] = v[0] + v[1] + ... + v[i]

Înseamnă că v[k] se va aduna la toate sumele s[k], s[k+1], ..., s[n]. Ceea ce înseamnă că dacă pe poziția k în vectorul v[] avem valoarea unu, acea valoare se va propaga în toate elementele lui s[] începând cu poziția k.

Dorim să aplicăm un interval [2, 13], deci vom plasa 1 pe poziția 2. El se va propaga până la finalul vectorului s[]. Dar noi vrem ca începând cu poziția 14 acel 1 să nu se mai propage. Deoarece nu putem acest lucru, vom face altceva: vom plasa valoarea -1 pe poziția 14. Ea se va propaga, și ea, până la final de vector s[], adunându-se la fiecare element o singură dată. Ea va anula propagarea elementului 1 plasat la poziția 2.

Similar, dacă dorim să aplicăm intervalul [6, 9] vom plasa 1 pe poziția 6 în v[] și -1 pe poziția 10.

După ce am plasat toate intervalele, vom calcula în s[] sumele parțiale ale lui v[]. Vectorul s[] este răspunsul, valorile finale cerute.

În fapt, nu avem nevoie de doi vectori. Putem suprascrie vectorul v[], deoarece nu mai avem nevoie de elementele marker.

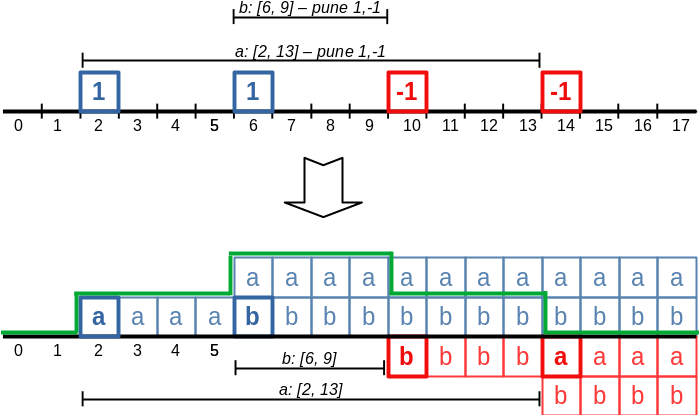
Funcţionează acest algoritm dacă avem capete de interval suprapuse? Da, cu condiţia ca elementul în care se suprapun capete să fie suma acelor capete, adică o sumă de 1 şi -1. Aceasta înseamnă că atunci când generăm vectorul de paranteze nu vom scrie s[i] = 1 ci s[i]++ (la fel şi pentru -1, vom decrementa).

Generalizare 1: putem generaliza această metodă pentru problema în care intervalele nu adună 1, ci orice număr, constant pe parcursul intervalului. Cum generalizăm? O paranteză deschisă nu va aduna 1, ci constanta respectivă.

Generalizare 2: dar dacă vectorul iniţial are valori diferite de zero? În acest caz vom calcula un vector separat, iniţializat cu zero, pe care facem calculul sumelor parţiale. Acest vector ne va spune cu cât s-a mărit fiecare element zero. În final vom aduna acest vector de sume parţiale la vectorul iniţial.

Acest exemplu de precalculare, este cunoscut printre unii din voi drept șmenul lui Mars, denumire care îmi displace deoarece sugerează că informatica este o colecție de șmenuri.

Când nu funcţionează această soluţie?

Atunci când coordonatele intervalelor sunt prea mari pentru ca vectorul de sume parţiale să încapă în memorie.

Să presupunem că ni se cere numărul maxim din vectorul de sume parţiale. În acest caz există o soluţie alternativă, mai generală (în sensul în care rezolvă o clasă mai mare de probleme cu intervale), care nu folosește precalculare: putem memora capetele de intervale, pe care apoi le ordonăm crescător, ţinând minte de ce tip sunt, închis sau deschis.

Apoi le parcurgem în ordine, calculînd sumele parţiale fără să le stocăm. Suma parţială maximă este răspunsul cerut.

Desigur că atunci când vectorul încape în memorie, e mai uşoară precalcularea.

Avantaje: cod mai rapid.
Schimbă complexitatea algoritmului: da.
Timp precalculare: O(k) - k numărul de intervale.
Memorie extra folosită: O(MAXCOORD). Poate fi prohibitiv dacă MAXCOORD este mare.

Matrice de differențe (difference arrays 2D)

Mai poartă denumirea de sume de dreptunghiuri

Acest tip de precalculare se poate extinde în două dimensiuni, pe matrice: se dau m dreptunghiuri care adună 1 la toate elementele respective dintr-o matrice. De data aceasta vom folosi o matrice de sume parțiale, ce necesită O(n²) memorie.

Nu voi detalia algoritmul, iată partea de plasare a unui dreptunghi (l1, c1) -> (l2, c2). Desenul arată punctele unde se adună/scade 1:

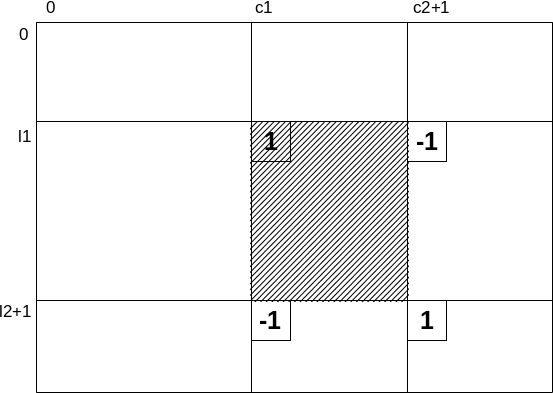
Această metodă nu se justifică decât în măsura în care este facil de programat, deoarece avem o soluție de aceeași complexitate care folosește varianta 1D, pe vector, folosind doar O(n) memorie, ca la problema flori1.

Exemple de probleme cu precalculare

Paisprezece: necesită un vector ce păstrează numere prime, ciurul lui Eratostene.
Intervale: ciurului lui Eratostene, sume parţiale.
Reginald, o optimizare a problemei anterioare.
Puncte1: o rezolvare posibilă folosește precalcularea sumelor parţiale ale unei matrice
Extraterestri precalculare vector sume prefixe parțiale (a.k.a. șmenul lui Mars)
Extraterestri1 Mars + normalizare coordonate
Flori Precalculare matrice sume prefixe parţiale (a.k.a. şmenul lui Mars 2D)
Flori1 exemplu de problemă nerezolvabilă cu precalculare 2D din lipsă de memorie

Concluzii

Precalcularea foloseşte atunci când avem de răspuns la mai multe întrebări costisitoare. Aceste întrebări pot fi explicite, cerute de enunţ, sau implicite, decurgând din metoda de rezolvare.
Precalcularea poate folosi şi atunci când numărul de întrebări este mult mai mare decât numărul de răspunsuri posibile, caz în care putem precalcula toate răspunsurile într-un tabel înainte de a răspunde la întrebări. Această precalculare seamănă cu memoizarea. Diferența constă în faptul că precalcularea este executată explicit înainte de calcul, pe când memoizarea ține minte valori calculate în timpul calculului.
Precalcularea foloseşte o structură de date adiţională şi memorie suplimentară. Uneori putem economisi memorie folosindu-ne chiar de structura de date iniţială.

Tema 5

Să se rezolve următoarele probleme (program C trimis la NerdArena):

Intervale dată pregătire OJI 2013 clasa a 9-a la Vianu
Patrate1 dată la cercul de informatică Vianu 2013 clasa a 6-a rezolvată în cel mult O(n³)!
Extraterestri dată la OJI 2012 clasa a 8-a

Tema opțională

Să se rezolve următoarele probleme (program C trimis la NerdArena):

Reginald dată la pregătire olimpiadă 2013 clasele 7/8/9/10 la Vianu
Flori1 dată la pregătire baraj gimnaziu 2013 la Vianu

Opțional, gândiți-vă la următoarele întrebări - calcul număr biți 1 în reprezentarea binară a unui întreg:

Se poate mai bine decât O(nr. biţi) fără memorie suplimentară (adică O(1) memorie suplimentară)?
Putem adapta metoda precalculării și la numere xMax mari, gen numere întregi pe int?

Accesează rezolvarea temei 5