Clasa a 7-a Lecția 27: Algoritmul Union-Find: Difference between revisions
(Created page with "== Înregistrare video lecție == {{#ev:youtube|https://youtu.be/QCaiWycJljs|||||start=8250&end=8320&loop=1}} == Problema Disjoint == Se dau <tt>N</tt> mulţimi de numere, iniţial fiecare mulţime <tt>i</tt> conţinând un singur element, mai exact elementul i. Asupra acestor mulţimi se pot face 2 tipuri de operaţii, astfel: * operaţia de tipul 1: se dau două numere naturale <tt>x</tt> si <tt>y</tt>, între 1 şi <tt>N</tt>. Se cere să se reunească m...") |
No edit summary |
||
| Line 67: | Line 67: | ||
=== Soluție forță brută === | === Soluție forță brută === | ||
O soluție posibilă ar fi ca pentru fiecare | O soluție posibilă ar fi ca pentru fiecare număr <tt>i</tt> să memorăm mulțimea din care face el parte. Astfel, <source lang="C" enclose="none">m[i]</source> va conține numărul mulțimii lui <tt>i</tt>. Dacă <tt>i</tt> și <tt>j</tt> fac parte din aceeași mulțime atunci <source lang="C" enclose="none">m[i] = m[j]</source>, în caz contrar <source lang="C" enclose="none">m[i] ≠ m[j]</source>. | ||
Inițial fiecare număr va avea propria lui mulțime, adică <source lang="C" enclose="none">m[i] = i</source>. | |||
==== Operația Find ==== | ==== Operația Find ==== | ||
Precum am spus, | Precum am spus, <tt>find(i)</tt> ne va da un identificator unic al mulțimii elementului <tt>i</tt>. În cazul nostru el va fi un număr între 0 și <tt>N-1</tt>. Cum o implementăm? Returnând chiar <source lang="C" enclose="none">m[i]</source>! | ||
<syntaxhighlight lang="c" line> | |||
int find( int i ) { | int find( int i ) { | ||
return m[i]; | return m[i]; | ||
} | } | ||
</syntaxhighlight> | |||
Ce complexitate are această operație? | Ce complexitate are această operație? | ||
Desigur ''O(1)''. | |||
==== Operația Union ==== | ==== Operația Union ==== | ||
Operația <tt>union(i, j)</tt> trebuie să reunească mulțimile din care fac parte elementele <tt>i</tt>, respectiv <tt>j</tt>. Cum o implementăm? Suprascriind identificatorul mulțimii lui <tt>j</tt> cu identificatorul mulțimii lui <tt>i</tt>, peste tot unde apare el. | |||
<syntaxhighlight lang="c" line> | |||
void union( int i, int j ) { | void union( int i, int j ) { | ||
int k, mj = m[j]; | int k, mj = m[j]; | ||
for ( k = 0; k | for ( k = 0; k < N; k++ ) | ||
if ( m[k] == mj ) | |||
m[k] = m[i]; | |||
} | |||
</syntaxhighlight> | |||
Ce complexitate are această operație? | Ce complexitate are această operație? | ||
Desigur ''O(N)''. | |||
''' Concluzie ''' | ''' Concluzie ''' | ||
| Line 100: | Line 112: | ||
Cu forța brută vom avea complexitățile: | Cu forța brută vom avea complexitățile: | ||
Find: | * Find: ''O(1)'' timp. | ||
* Union: ''O(N)'' timp. | |||
Union: | * Memorie necesară: ''O(N)''. | ||
Memorie necesară: | |||
| Line 111: | Line 121: | ||
Să încercăm să optimizăm operația union. Actualizarea identificatorilor mulțimii durează mult. Ce putem face? | Să încercăm să optimizăm operația union. Actualizarea identificatorilor mulțimii durează mult. Ce putem face? | ||
O idee ar fi ca, în loc să actualizăm toți identificatorii mulțimii | O idee ar fi ca, în loc să actualizăm toți identificatorii mulțimii lui <tt>j</tt>, să îl actualizăm doar pe al lui <tt>j</tt>. Astfel, fiecare element între 0 și <tt>N-1</tt> va ţine mine un şef al său din mulţime. Întocmai ca într-o companie, fiecare element al unei submulţimi va raporta unui şef, şefii vor raporta altor şefi şi aşa mai departe până ce se ajunge la şeful unic, conducătorul submulţimii. El nu are şef şi este considerat reprezentantul acelei submulţimi. | ||
Cum memorăm acest lucru? Printr-un simplu vector de şefi (similar | Cum memorăm acest lucru? Printr-un simplu vector de şefi (similar vectorului <source lang="C" enclose="none">m[]</source>) în care elementul <source lang="C" enclose="none">sef[i]</source> este numărul din mulţimea 0..N-1 care este şeful lui <tt>i</tt>. Ce punem în elementele şefi supremi, cele care nu au șefi? Pentru a le distinge de elementele subalterni fiecare şef suprem este propriul lui şef. Dacă elementul <tt>i</tt> este şef suprem atunci <source lang="C" enclose="none">sef[i] = i</source>. O alternativă la această reprezentare, dacă ''sacrificăm'' elementul 0, este să memorăm zero ca şef fictiv pentru elementele reprezentative ale mulţimilor. | ||
Inițial fiecare element este propriul său șef. Atunci când căutăm o mulțime, căutăm de fapt șeful suprem, care este propriul său șef. Când unificăm mulțimile | Inițial fiecare element este propriul său șef. Atunci când căutăm o mulțime, căutăm de fapt șeful suprem, care este propriul său șef. Când unificăm mulțimile lui <tt>i</tt> și ale lui <tt>j</tt> vom nota că șeful mulțimii <tt>i</tt> devine șeful șefului mulțimii <tt>j</tt>. | ||
==== Operația Find ==== | ==== Operația Find ==== | ||
Precum am spus, | Precum am spus, <tt>find(i)</tt> va returna șeful mulțimii din care face parte <tt>i</tt>. Cum îl găsim? Mergând la șeful lui <tt>i</tt>, apoi la șeful șefului lui <tt>i</tt> și tot așa până la șeful mulțimii. Iată o implementare recursivă simplă: | ||
<syntaxhighlight lang="c" line> | |||
int find( int i ) { | int find( int i ) { | ||
if ( sef[i] == i ) // daca am gasit seful suprem | if ( sef[i] == i ) // daca am gasit seful suprem | ||
| Line 127: | Line 138: | ||
return find( sef[i] ); // altfel returnam seful sefului | return find( sef[i] ); // altfel returnam seful sefului | ||
} | } | ||
</syntaxhighlight> | |||
Ce complexitate are această operație? | Ce complexitate are această operație? | ||
Care este cazul cel mai rău? Când toate elementele se înșiră într-un lanț lung de șefi. În acest caz timpul | Care este cazul cel mai rău? Când toate elementele se înșiră într-un lanț lung de șefi. În acest caz timpul este ''O(N)''. | ||
==== Operația Union ==== | ==== Operația Union ==== | ||
Operația <tt>union(i, j)</tt> trebuie să reunească mulțimile din care fac parte elementele <tt>i</tt>, respectiv <tt>j</tt>. Cum o implementăm? Suprascriind identificatorul mulțimii lui <tt>j</tt> cu identificatorul mulțimii lui <tt>i</tt>, peste tot unde apare el. | |||
<syntaxhighlight lang="c" line> | |||
void union( int i, int j ) { | void union( int i, int j ) { | ||
int sefi, sefj; | int sefi, sefj; | ||
| Line 145: | Line 159: | ||
sef[sefj] = sefi; // seful suprem al lui sefj devine sefi | sef[sefj] = sefi; // seful suprem al lui sefj devine sefi | ||
} | } | ||
</syntaxhighlight> | |||
Ce complexitate are această operație? | Ce complexitate are această operație? | ||
Ea apelează de două | Ea apelează de două ori <tt>find()</tt>, iar apoi face ''O(1)'' operații. | ||
| Line 155: | Line 171: | ||
Cu soluția alternativă avem complexitățile: | Cu soluția alternativă avem complexitățile: | ||
Find: | * Find: ''O(N)'' timp. | ||
* Union: ''O(1)'' timp + complexitatea lui Find. | |||
Union: | * Memorie necesară: ''O(N)''. | ||
Memorie necesară: | |||
Nu pare că am avansat, nu? Poate că nu. Observăm, însă, că timpul total depinde de Find: dacă reușim să îmbunătățim complexitatea lui Find automat vom îmbunătăți și complexitatea lui Union. | Nu pare că am avansat, nu? Poate că nu. Observăm, însă, că timpul total depinde de Find: dacă reușim să îmbunătățim complexitatea lui Find automat vom îmbunătăți și complexitatea lui Union. | ||
Putem îmbunătăți timpul | Putem îmbunătăți timpul lui find la ''O(log N)'' cu o modificare destul de mică a structurii de date, dar nu voi prezenta acest lucru. Pentru cei curioși, putem memora cea mai lungă cale de șefi din fiecare mulțime, iar apoi vom atașa mulțimea mai mică la cea mai mare (alegând în mod potrivit dacă atașăm șeful lui <tt>i</tt> la <tt>j</tt> sau invers). | ||
=== Soluție eficientă folosind compresia căii === | === Soluție eficientă folosind compresia căii === | ||
Pentru a obţine cel mai eficient algoritm cunoscut avem nevoie de două optimizări: compresia căii și menținerea unui rang al fiecărei mulțimi. Voi prezenta aici doar una dintre ele, cea mai importantă, compresia căii. Ea face un lucru foarte simplu: schimbă puţin funcţia find ca, atunci când dorim să aflăm care este şeful | Pentru a obţine cel mai eficient algoritm cunoscut avem nevoie de două optimizări: compresia căii și menținerea unui rang al fiecărei mulțimi. Voi prezenta aici doar una dintre ele, cea mai importantă, compresia căii. Ea face un lucru foarte simplu: schimbă puţin funcţia find ca, atunci când dorim să aflăm care este şeful nodului <tt>i</tt>, să lege toţi şefii parcurşi direct la şeful suprem. Cu alte cuvinte vom parcurge aceiaşi şefi intermediari până la şeful suprem, dar odată găsit va trebui să ne întoarcem la şefii intermediari şi să le schimbăm şeful. Aceasta duce aproximativ la o dublare a opreaţiilor efectuate de find. Dar, precum spunea astronatul Neil Armstrong, un pas mic pentru un om poate fi un pas uriaş pentru omenire. O mică modificare ce duce la dublarea timpului lui find duce la o scurtare fantastică a următoarelor operaţiuni ''find''. | ||
[[File:path-compression-find.png|frame|none|Exemplu de ''find'' cu compresia căii]] | |||
Această optimizare poartă denumirea de compresia căii, sau, în engleză, path compression. | Această optimizare poartă denumirea de compresia căii, sau, în engleză, path compression. | ||
| Line 177: | Line 193: | ||
Iată o modificare mică a funcției anterioare, care face și compresia căii: | Iată o modificare mică a funcției anterioare, care face și compresia căii: | ||
<syntaxhighlight lang="c" line> | |||
int find( int i ) { | int find( int i ) { | ||
if ( sef[i] == i ) // daca am gasit seful suprem | if ( sef[i] == i ) // daca am gasit seful suprem | ||
| Line 182: | Line 199: | ||
return sef[i] = find( sef[i] ); // altfel legam i la seful suprem, pe care il si returnam | return sef[i] = find( sef[i] ); // altfel legam i la seful suprem, pe care il si returnam | ||
} | } | ||
</syntaxhighlight> | |||
==== Operația Union ==== | ==== Operația Union ==== | ||
Operația <tt>union(i, j)</tt> trebuie să reunească mulțimile din care fac parte elementele <tt>i</tt>, respectiv <tt>j</tt>. Cum o implementăm? Suprascriind identificatorul mulțimii lui <tt>j</tt> cu identificatorul mulțimii lui <tt>i</tt>, peste tot unde apare el. | |||
<syntaxhighlight lang="c" line> | |||
void union( int i, int j ) { | void union( int i, int j ) { | ||
int sefi, sefj; | int sefi, sefj; | ||
| Line 196: | Line 215: | ||
sef[sefj] = sefi; // seful suprem al lui sefj devine sefi | sef[sefj] = sefi; // seful suprem al lui sefj devine sefi | ||
} | } | ||
</syntaxhighlight> | |||
Ce complexitate au aceste operații? | Ce complexitate au aceste operații? | ||
În această implementare, ele | În această implementare, ele sunt ''O(log N)'' amortizat, per operație, cu o constantă foarte mică. Demonstrația acestui lucru depășește cadrul acestui curs. | ||
| Line 206: | Line 226: | ||
Cu compresia căii avem complexitățile: | Cu compresia căii avem complexitățile: | ||
Find: | * Find: ''O(log N)'' timp. | ||
* Union: ''O(log N)'' timp. | |||
* Memorie necesară: ''O(N)''. | |||
Notă: se poate mai bine. Dacă adăugăm și cealaltă optimizare menționată mai sus, rangul unei mulțimi, ajungem la o complexitate ''O(α(N))'', unde ''α(N)'' este inversul funcției lui Ackermann, o funcție rapid crescătoare. Cu această modificare timpul amortizat este, practic, constant. | |||
Notă: se poate mai bine. Dacă adăugăm și cealaltă optimizare menționată mai sus, rangul unei mulțimi, ajungem la o | |||
=== Inversarea sensului === | === Inversarea sensului === | ||
Ocazional veți întâlni problema inversă: se pornește cu o structură conexă care, treptat, este deconectată. Pe parcurs, se cer informații despre conexitate. Aceasta este o problemă | Ocazional veți întâlni problema inversă: se pornește cu o structură conexă care, treptat, este deconectată. Pe parcurs, se cer informații despre conexitate. Aceasta este o problemă de '''partiționare''', care nu admite o soluție directă la fel de simplă. | ||
Dar, când memoria permite stocarea șirului de operații, o soluție este: | Dar, când memoria permite stocarea șirului de operații, o soluție este: | ||
Executăm toate operațiile de deconectare, obținând structura finală. | * Executăm toate operațiile de deconectare, obținând structura finală. | ||
* Executăm în ordine inversă operațiile, care acum reconectează structura. Putem face aceste operații cu structuri de mulțimi disjuncte. | |||
Executăm în ordine inversă operațiile, care acum reconectează structura. Putem face aceste operații cu structuri de mulțimi disjuncte. | * Notăm răspunsurile la interogările de conexitate. | ||
* Tipărim aceste răspunsuri în ordine inversă. | |||
Notăm răspunsurile la interogările de conexitate. | |||
Tipărim aceste răspunsuri în ordine inversă. | |||
Exemple de astfel de probleme: bile3, | Exemple de astfel de probleme: [https://www.nerdarena.ro/problema/bile3 Bile3], [https://www.nerdarena.ro/problema/ruine Ruine], pe care le aveți la temă, respectiv tema opțională. | ||
Latest revision as of 15:30, 10 June 2025
Înregistrare video lecție
Problema Disjoint
Se dau N mulţimi de numere, iniţial fiecare mulţime i conţinând un singur element, mai exact elementul i. Asupra acestor mulţimi se pot face 2 tipuri de operaţii, astfel:
- operaţia de tipul 1: se dau două numere naturale x si y, între 1 şi N. Se cere să se reunească mulţimile în care se află elementul x, respectiv elementul y (se garantează că x si y nu se vor afla în aceeaşi mulţime).
- operaţia de tipul 2: se dau două numere naturale x si y, între 1 şi N. Se cere să se afişeze DA dacă cele 2 elemente se află în aceeaşi mulţime, respectiv NU în caz contrar.
Date de intrare
Pe prima linie a fişierului de intrare disjoint.in se vor afla 2 numere, N şi M, reprezentând numărul de mulţimi, respectiv numărul de operaţii efectuate. Pe următoarele M linii se vor afla câte 3 numere, cod, x si y, cod reprezentând tipul operaţiei, iar x si y având semnificaţia din enunţ.
Date de ieşire
În fişierul de ieşire disjoint.out se vor afişa mai multe linii, fiecare linie conţinând DA sau NU, reprezentând răspunsul la interogarea corespunzătoare din fişierul de intrare.
Restricţii
- 1 ≤ N ≤ 100 000
- 1 ≤ M ≤ 100 000
Exemplu
| disjoint.in | disjoint.out |
|---|---|
|
4 6 |
NU |
Algoritmul union-find
Problema Disjoint şi rezolvarea ei, este o unealtă foarte utilă din trusa de scule a algoritmistului. Să definim problema:
Dată o mulţime A de valori de la 0 la N-1 definim submulţimi disjuncte pe această mulţime, astfel încât aceste submulţimi să acopere mulţimea originală A. Apoi începem să reunim unele dintre aceste mulţimi. Reuniunea se face menţionând două elemente ale submulţimilor ce se doresc reunite (dacă elementele se găsesc deja în aceeaşi submulţime nu vom face nimic). După ce efectuăm aceste operaţii de reuniune dorim să răspundem la întrebarea ce submulţimi avem?.
Cu alte cuvinte, cunoscând N şi ştiind că iniţial fiecare număr face parte din propria submulţime şi apoi dându-se mai multe perechi de numere (ai, aj) cu semnificaţia mulţimea din care face parte ai se reuneşte cu mulţimea din care face parte aj trebuie ca în final să spunem ce submulţimi există.
Pentru a implementa algoritmul vom avea nevoie de două operaţii:
- reuneşte două mulţimi (union)
- găseşte mulţimea unui element (find)
De aici şi denumirea problemei union-find. În română se regăseşte sub numele de colecţie de mulţimi disjuncte, dar se folosesc și denumirile DSU (disjoint set union) sau union-find.
Soluție forță brută
O soluție posibilă ar fi ca pentru fiecare număr i să memorăm mulțimea din care face el parte. Astfel, m[i] va conține numărul mulțimii lui i. Dacă i și j fac parte din aceeași mulțime atunci m[i] = m[j], în caz contrar m[i] ≠ m[j].
Inițial fiecare număr va avea propria lui mulțime, adică m[i] = i.
Operația Find
Precum am spus, find(i) ne va da un identificator unic al mulțimii elementului i. În cazul nostru el va fi un număr între 0 și N-1. Cum o implementăm? Returnând chiar m[i]!
int find( int i ) {
return m[i];
}
Ce complexitate are această operație?
Desigur O(1).
Operația Union
Operația union(i, j) trebuie să reunească mulțimile din care fac parte elementele i, respectiv j. Cum o implementăm? Suprascriind identificatorul mulțimii lui j cu identificatorul mulțimii lui i, peste tot unde apare el.
void union( int i, int j ) {
int k, mj = m[j];
for ( k = 0; k < N; k++ )
if ( m[k] == mj )
m[k] = m[i];
}
Ce complexitate are această operație?
Desigur O(N).
Concluzie
Cu forța brută vom avea complexitățile:
- Find: O(1) timp.
- Union: O(N) timp.
- Memorie necesară: O(N).
Soluție alternativă
Să încercăm să optimizăm operația union. Actualizarea identificatorilor mulțimii durează mult. Ce putem face?
O idee ar fi ca, în loc să actualizăm toți identificatorii mulțimii lui j, să îl actualizăm doar pe al lui j. Astfel, fiecare element între 0 și N-1 va ţine mine un şef al său din mulţime. Întocmai ca într-o companie, fiecare element al unei submulţimi va raporta unui şef, şefii vor raporta altor şefi şi aşa mai departe până ce se ajunge la şeful unic, conducătorul submulţimii. El nu are şef şi este considerat reprezentantul acelei submulţimi.
Cum memorăm acest lucru? Printr-un simplu vector de şefi (similar vectorului m[]) în care elementul sef[i] este numărul din mulţimea 0..N-1 care este şeful lui i. Ce punem în elementele şefi supremi, cele care nu au șefi? Pentru a le distinge de elementele subalterni fiecare şef suprem este propriul lui şef. Dacă elementul i este şef suprem atunci sef[i] = i. O alternativă la această reprezentare, dacă sacrificăm elementul 0, este să memorăm zero ca şef fictiv pentru elementele reprezentative ale mulţimilor.
Inițial fiecare element este propriul său șef. Atunci când căutăm o mulțime, căutăm de fapt șeful suprem, care este propriul său șef. Când unificăm mulțimile lui i și ale lui j vom nota că șeful mulțimii i devine șeful șefului mulțimii j.
Operația Find
Precum am spus, find(i) va returna șeful mulțimii din care face parte i. Cum îl găsim? Mergând la șeful lui i, apoi la șeful șefului lui i și tot așa până la șeful mulțimii. Iată o implementare recursivă simplă:
int find( int i ) {
if ( sef[i] == i ) // daca am gasit seful suprem
return i; // il returnam
return find( sef[i] ); // altfel returnam seful sefului
}
Ce complexitate are această operație?
Care este cazul cel mai rău? Când toate elementele se înșiră într-un lanț lung de șefi. În acest caz timpul este O(N).
Operația Union
Operația union(i, j) trebuie să reunească mulțimile din care fac parte elementele i, respectiv j. Cum o implementăm? Suprascriind identificatorul mulțimii lui j cu identificatorul mulțimii lui i, peste tot unde apare el.
void union( int i, int j ) {
int sefi, sefj;
sefi = find( i ); // seful suprem al lui i
sefj = find( j ); // seful suprem al lui j
sef[sefj] = sefi; // seful suprem al lui sefj devine sefi
}
Ce complexitate are această operație?
Ea apelează de două ori find(), iar apoi face O(1) operații.
Concluzie
Cu soluția alternativă avem complexitățile:
- Find: O(N) timp.
- Union: O(1) timp + complexitatea lui Find.
- Memorie necesară: O(N).
Nu pare că am avansat, nu? Poate că nu. Observăm, însă, că timpul total depinde de Find: dacă reușim să îmbunătățim complexitatea lui Find automat vom îmbunătăți și complexitatea lui Union.
Putem îmbunătăți timpul lui find la O(log N) cu o modificare destul de mică a structurii de date, dar nu voi prezenta acest lucru. Pentru cei curioși, putem memora cea mai lungă cale de șefi din fiecare mulțime, iar apoi vom atașa mulțimea mai mică la cea mai mare (alegând în mod potrivit dacă atașăm șeful lui i la j sau invers).
Soluție eficientă folosind compresia căii
Pentru a obţine cel mai eficient algoritm cunoscut avem nevoie de două optimizări: compresia căii și menținerea unui rang al fiecărei mulțimi. Voi prezenta aici doar una dintre ele, cea mai importantă, compresia căii. Ea face un lucru foarte simplu: schimbă puţin funcţia find ca, atunci când dorim să aflăm care este şeful nodului i, să lege toţi şefii parcurşi direct la şeful suprem. Cu alte cuvinte vom parcurge aceiaşi şefi intermediari până la şeful suprem, dar odată găsit va trebui să ne întoarcem la şefii intermediari şi să le schimbăm şeful. Aceasta duce aproximativ la o dublare a opreaţiilor efectuate de find. Dar, precum spunea astronatul Neil Armstrong, un pas mic pentru un om poate fi un pas uriaş pentru omenire. O mică modificare ce duce la dublarea timpului lui find duce la o scurtare fantastică a următoarelor operaţiuni find.
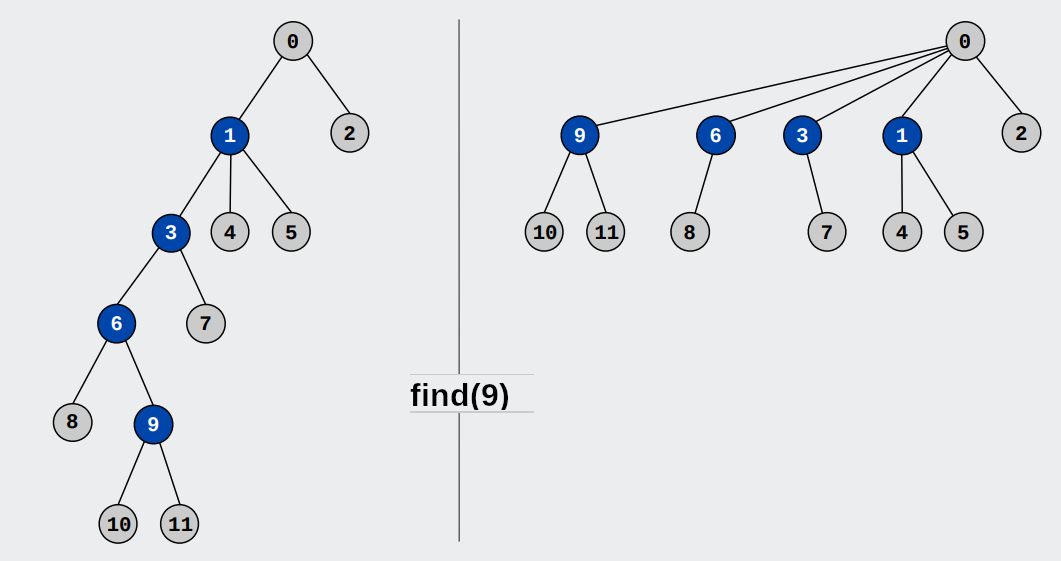
Această optimizare poartă denumirea de compresia căii, sau, în engleză, path compression.
Operația Find
Iată o modificare mică a funcției anterioare, care face și compresia căii:
int find( int i ) {
if ( sef[i] == i ) // daca am gasit seful suprem
return i; // il returnam
return sef[i] = find( sef[i] ); // altfel legam i la seful suprem, pe care il si returnam
}
Operația Union
Operația union(i, j) trebuie să reunească mulțimile din care fac parte elementele i, respectiv j. Cum o implementăm? Suprascriind identificatorul mulțimii lui j cu identificatorul mulțimii lui i, peste tot unde apare el.
void union( int i, int j ) {
int sefi, sefj;
sefi = find( i ); // seful suprem al lui i
sefj = find( j ); // seful suprem al lui j
sef[sefj] = sefi; // seful suprem al lui sefj devine sefi
}
Ce complexitate au aceste operații?
În această implementare, ele sunt O(log N) amortizat, per operație, cu o constantă foarte mică. Demonstrația acestui lucru depășește cadrul acestui curs.
Concluzie
Cu compresia căii avem complexitățile:
- Find: O(log N) timp.
- Union: O(log N) timp.
- Memorie necesară: O(N).
Notă: se poate mai bine. Dacă adăugăm și cealaltă optimizare menționată mai sus, rangul unei mulțimi, ajungem la o complexitate O(α(N)), unde α(N) este inversul funcției lui Ackermann, o funcție rapid crescătoare. Cu această modificare timpul amortizat este, practic, constant.
Inversarea sensului
Ocazional veți întâlni problema inversă: se pornește cu o structură conexă care, treptat, este deconectată. Pe parcurs, se cer informații despre conexitate. Aceasta este o problemă de partiționare, care nu admite o soluție directă la fel de simplă.
Dar, când memoria permite stocarea șirului de operații, o soluție este:
- Executăm toate operațiile de deconectare, obținând structura finală.
- Executăm în ordine inversă operațiile, care acum reconectează structura. Putem face aceste operații cu structuri de mulțimi disjuncte.
- Notăm răspunsurile la interogările de conexitate.
- Tipărim aceste răspunsuri în ordine inversă.
Exemple de astfel de probleme: Bile3, Ruine, pe care le aveți la temă, respectiv tema opțională.
Tema 27
Să se rezolve următoarele probleme (program C trimis la NerdArena):
Tema opțională
Să se rezolve următoarele probleme (program C trimis la NerdArena):