Latest revision as of 18:06, 14 October 2018

Lecție

Prelucrarea secventelor de n numere

Secvență monotonă

Rezolvați problema monotonă: numim o secvență monotonă dacă ea este fie crescătoare fie descrescătoare. O secvență este crescătoare dacă fiecare element este mai mare sau egal cu cel dinaintea lui. O secvență este descrescătoare dacă fiecare element este mai mic sau egal cu cel dinaintea lui. Cerință: dată o secvență de n numere să se spună dacă este monotonă. Exemple:

Fișierul `monotona.in`	Fișierul `monotona.out`	Explicație
`5 4 7 7 8 8`	`da`	Secvența este crescătoare.
`8 7 7 7 7 4 4 3 2`	`da`	Secvența este descrescătoare.
`6 3 3 3 3 3 3`	`da`	Secvența poate fi și crescătoare si descrescătoare.
`8 1 1 1 2 2 2 1 2`	`nu`	Secvența nu este nici crescătoare nici descrescătoare.

Răspuns: La începutul secvenței nu știm în ce stare se află ea: este crescătoare sau descrescătoare, sau nici una, nici alta. O idee ar putea fi să ne uităm la primele două numere din secvență și să stabilim. Din păcate acest lucru nu este posibil deoarece primele două numere pot fi egale. Sau primele 10 numere!

O altă idee ar putea fi să citim numere pînă ce găsim un număr diferit de primul. Dar trebuie să avem grijă să nu se termine secvența înainte! Puteți să încercați voi soluția aceasta, probabil că unii dintre voi așa vor încerca.

Aici vom descrie o altă soluție: vom folosi o variabilă d care ne va indica direcția de creștere a secvenței: d va fi:

1 dacă secvența este crescătoare
-1 dacă secvența este descrescătoare
0 dacă secvența este egală, compusă din același număr
2 dacă secvența nu este în nici unul din cazurile de mai sus (adică nu este nici crescătoare, nici egală nici descrescătoare)

La început, înainte să citim numere, secvența este egală, deci vom inițializa d cu 0. Pe măsură ce citim numere vom vedea cum se compară cu cele din-naintea lor și vom modifica d ca atare. Dacă găsim un număr mai mic înseamnă că secvența a devenit descrescătoare, deci vom pune d pe -1. Dacă găsim un număr mai mare, înseamnă că punem d pe 1. Dacă însă d este deja -1, adică secvența este descrescătoare, și găsim un număr mai mare, înseamnă că secvența întîi a scăzut și apoi crește, deci nu este monotonă și vom pune d 2. Similar, dacă d este deja 1 și apoi găsim un număr mai mic, vom pune d pe 2. La final secvența va fi monotonă dacă d < 2.

Iată algoritmul care implementează această idee.

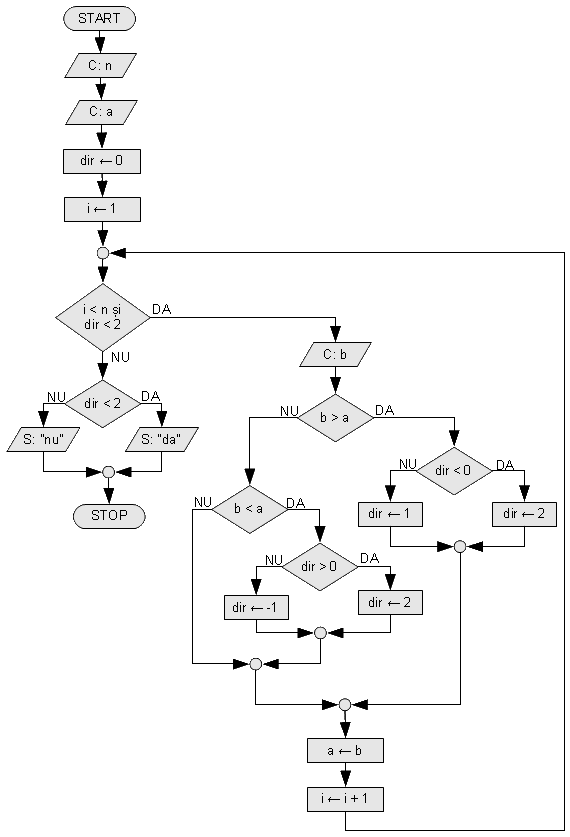#include <stdio.h>
int main() {
  FILE *fin, *fout;
  int n, i, a, b, dir;

  fin = fopen( "monotona.in", "r" );
  fscanf( fin, "%d", &n );
  fscanf( fin, "%d", &a );
  /*
    directia poate fi:
    -1 - descrescatoare
     0 - indecisa (egala)
     1 - crescatoare
     2 - nici unul din cazurle de mai sus
  */
  dir = 0; // initial directia este indecisa (egala)
  i = 1;
  while ( i < n && dir < 2 ) {
    fscanf( fin, "%d", &b );
    if ( b > a ) // secventa devine crescatoare, daca se mai poate
      if ( dir < 0 )
        dir = 2;
      else
        dir = 1;
    else if ( b < a ) // secventa devine descrescatoare, daca se mai poate
      if ( dir > 0 )
        dir = 2;
      else
        dir = -1;
    a = b;
    i++;
  }
  fclose( fin );

  fout = fopen( "monotona.out", "w" );
  if ( dir < 2 )
    fprintf( fout, "da\n" );
  else
    fprintf( fout, "nu\n" );
  fclose( fout );
  return 0;
}

O alta varianta de rezolvare :

#include <stdio.h>

int main() {
  int n, a, b, i, cresc, monoton;
  scanf( "%d%d%d", &n, &a, &b ); // n si primele doua numere
  i = 2;
  // Ignoram toate elemente egale de la inceput, pt a stabili monotonia sirului
  while (i < n && a == b) {
    scanf("%d", &b);
    i++;
  }
  // Daca sirul este crescator, monoton = 1; Altfel, monoton = -1.
  cresc = monoton = (a < b) ? 1 : -1;
  // Cat timp nu am terminat si este pastrata monotonia initiala
  while (i < n && monoton == cresc) {
      a = b;
      scanf("%d", &b);
      if (a < b)
        cresc = 1;
      else if (a > b)
        cresc = -1;
      i++;
  }
  if (monoton == cresc)
    printf("DA");
  else
    printf("NU");

  return 0;
}

Paranteze

Dată o secvență de 0 și 1, unde 0 înseamnă paranteză deschisă '(', iar 1 înseamnă paranteză închisă ')', spuneți dacă secvența reprezintă o expresie corectă de paranteze și dacă da calculați numărul maxim de paranteze una într-alta. Exemplu: 0 1 0 0 1 0 1 1 este corectă și are factorul de imbricare de 2, pe cînd secvența 0 0 0 1 1 1 0 este incorectă. Nu aveți voie să folosiți tablouri (vectori sau matrice).

Putem rezolva problema observînd următoarele reguli valabile pentru orice expresie corectă:

oriunde "rupem" expresia, în partea stîngă vom avea un număr de paranteze deschise mai mare sau egal cu cele închise
la final numărul de paranteze închise trebuie să fie egal cu cele închise

Dacă ambele condiții se îndeplinesc expresia e corectă. Prima condiție trebuie îndeplinită pentru fiecare poziție de rupere.

#include <stdio.h>

int main() {
  int n, a, i, nrdesc, max;

  scanf("%d", &n);
  max = nrdesc = i = 0;
  while ( i < n && nrdesc >= 0 ) {
    scanf( "%d", &a );
    if ( a == 0 ) {
      nrdesc++;
      if ( nrdesc > max )
        max = nrdesc;
    } else
      nrdesc--;
    i++;
  }
  if ( nrdesc == 0 )
    printf("Expresie corecta, factor de imbricare %d", max);
  else
    printf("Expresie incorecta");

  return 0;
}

Șirul lui Fibonacci

Definiție: șirul lui Fibonacci este secvența de numere 0, 1, 1, 2, 3, 5, 8, 13... Regula acestei secvențe este că primele două numere sînt 0 și 1, iar următoarele numere sînt suma celor două numere din-naintea lor. Exercițiu: dat n, să se calculeze al n-lea termen din șirul lui Fibonacci.

 #include <stdio.h>

 int main() {
   FILE *fin, *fout;
   int n, i, a, b, f;

   fin = fopen( "fibonacci.in", "r" );
   fscanf( fin, "%d", &n );
   fclose( fin );

   a = 0;
   if ( n == 1 )
     b = a;
   else {
     b = 1;
     for ( i = 2; i < n; i++ ) {
       f = a + b;
       a = b;
       b = f;
     }
   }

   fout = fopen( "fibonacci.out", "w" );
   fprintf( fout, "%d", b );
   fclose( fout );
   return 0;
 }

Numere identice

Se dă o secvența de n numere. Să se spună care este numărul maxim de numere identice consecutive în secvență. Exemple:

`identice.in`	`identice.out`	Explicație
`10 6 2 2 5 8 8 8 2 2 5`	`3`	Numărul 8 apare de trei ori la rînd. Nici un alt număr nu apare de mai multe ori la rînd.
`14 8 8 3 3 3 3 1 1 1 5 5 5 5 2`	`4`	Numărul 3 apare de patru ori la rînd. De asemenea și numărul 5 apare de patru ori la rînd. Nici un alt număr nu apare de mai multe ori la rînd.

Rezolvare:

 #include <stdio.h>

 int main() {
   FILE *fin, *fout;
   int n, i, a, b, l, lmax;

   fin = fopen( "identice.in", "r" );
   fscanf( fin, "%d", &n );
   fscanf( fin, "%d", &a );
   lmax = 1;
   l = 1;
   for ( i = 1; i < n; i++ ) {
     fscanf( fin, "%d", &b );
     if ( b == a ) {
       l++;
       if ( l > lmax )
         lmax = l;
     } else {
       a = b;
       l = 1;
     }
   }
   fclose( fin );

   fout = fopen( "identice.out", "w" );
   fprintf( fout, "%d", lmax );
   fclose( fout );
   return 0;
 }

Observații:

Și aici ținem minte elemetul anterior în secvență, pentru a-l putea compara cu cel actual.
O alternativă mai eficientă ar fi să comparăm l > lmax numai atunci cînd b ≠ a. Se poate și așa, dar trebuie să avem grijă în cazul în care cea mai lungă secvență este chiar la final. Pentru acest caz particular va trebui ca imediat după bucla WHILE-DO să mai testăm o dată dacă l > lmax.

Complexitatea algoritmilor ce prelucreaza secvente de n numere

Complexitatea de timp a acestor algoritmi este liniară, egală cu numărul de elemente ale secvenţei: O(n).Complexitatea de memorie este insa O(1). Dupa cum observam cele n numere vor fi prelucrate/analizate pe masura ce le citim, nefiind necesara memorarea tuturor valorilor.

Vectori de frecventa ( adaugat ulterior )

Culori

Se citește la intrare un număr n și apoi n culori. Cele n culori sînt codificate cu numere între 0 și 14. Să se afișeze în ordine crescătoare toate culorile care apar de cele mai multe ori în secvență.

Exemplu: pentru secvența

22
4 2 9 8 2 5 8 10 14 12 14 6 12 14 8 3 7 2 0 13 14 8

Vom afișa:

8 14

deoarece culorile 8 și 14 apar de 4 ori în secvență, iar toate celelalte culori apar de mai puține ori.

Rezolvare: vom crea un vector caracteristic a de 15 elemente, inițializat cu zero. Apoi vom citi rînd pe rînd culorile, în variabila c, adunînd 1 la a[c]. În final a[c] va conține numărul de apariții ale culorii c. Pentru a afla culorile care apar de cele mai multe ori vom căuta maximul în acest vector, apoi, la o a doua parcurgere vom afișa toate pozițiile pe care a[i] este maxim. Iată soluția:

#include <stdio.h>

int a[15];

int main() {
  FILE *fin, *fout;
  int n, i, c, max;

  // citim secventa de culori si construim vectorul de frecventa
  fin = fopen( "culori.in", "r" );
  fscanf( fin, "%d", &n );
  for ( i = 0; i < n; i++ ) {
    fscanf( fin, "%d", &c );
    a[c]++;
  }
  fclose( fin );

  // cautam maximul in vectorul de frecventa
  max = a[0];
  for ( c = 1; c < 15; c++ )
    if ( a[c] > max )
      max = a[c];

  // afisam toate pozitiile c pentru care a[c] == max
  fout = fopen( "culori.out", "w" );
  for ( c = 0; c < 15; c++ )
    if ( a[c] == max )
      fprintf( fout, "%d ", c );
  fclose( fout );

  return 0;
}

Temă -de revizuit

magic 1 dată la OJI 2011 clasa a 5^a
panglica dată la ONI 2002 clasa a 5^a

Complexitatea algoritmilor ce utilizeaza vectori de frecventa

Complexitatea de timp a acestui algoritm este liniară, egală cu numărul de elemente ale secvenţei: O(n). Complexitatea de memorie este O(k), unde k depinde de intervalul de apartenență al valorilor ce vor fi contorizate in vectorul de vrecventa, in problema de mai sus avem 15 culori distincte ( valorile de la 0 la 14 ), deci pentru problema de mai sus k = 15.

Vectori

În continuare vom discuta rezolvări ale unor probleme clasice cu vectori.

Căutare în vector

Se dă un vector v de n elemente și un extra element e. Să se găsească poziția p în v unde apare prima oară elementul e. Dacă elementul e nu apare p va avea valoarea n. O soluție elegantă care nu iese forțat din buclă și care nu folosește stegulețe este:

// avem vectorul v de n elemente si o valoare e de gasit in acest vector
p = 0;
while ( p < n && v[p] != e )
  p++;
// acum p este fie pozitia primei aparitii a lui e, fie n daca e nu exista in v

Inserare în vector

Se dă un vector v de n elemente, un extra element e și o poziție p. Să se insereze elementul e la poziția p. În final elementul e va fi pe poziția p în vector, iar elementele de la poziția p pînă la final vor fi deplasate spre final cu o poziție. Vom considera că p este o poziție validă, între 0 și n.

// avem vectorul v de n elemente si o valoare e de inserat la poziția p
for ( i = n - 1; i >= p; i-- ) // deplasăm elementele spre dreapta
  v[i+1] = v[i];
v[p] = e;
n++; // vectorul are acum n+1 elemente!

Ștergere din vector

Se dă un vector v de n elemente și o poziție p. Să se elimine elementul de la poziția p din vector. Elementele de la poziția p pînă la final se vor deplasa către începutul vectorului cu o poziție.

// avem vectorul v de n elemente si o poziție p ce trebuie eliminata
for ( i = p + 1; i < n; i++ ) // deplasam elementele spre stinga
  v[i-1] = v[i];
n--; // vectorul are acum n-1 elemente!

Cautare si Ștergere element

Dat un vector v și un element e să se elimine din vector prima apariție a elementului e, în caz că acesta apare în vector. Exemplu: v = 5 9 2 7 9 3 5 7 4 si e = 9, la final v = 5 2 7 9 3 5 7 4

Soluție incorectă

O soluție foarte populară este să căutăm elementul în vector și, în momentul cînd îl găsim să-l ștergem:

for ( i = 0; i < n; i++ )
  if ( v[i] == e ) {
    for ( j = i + 1; j < n; j++ )
      v[j-1] = v[j];
    i = n;
  }

Aceasta este o soluție urîtă deoarece:

folosește for pentru un ciclu cu număr necunoscut de pași
modifică variabila de ciclu, i
nu folosește "cărămizile" învățate deja și anume căutarea unui element în vector și ștergerea unui element din vector

Soluție corectă

Ștergerea unui element din vector se face astfel:

Vom avea două etape: căutare element în vector + eliminarea propriu zisă.
În final numărul de elemente n se micșorează cu unu.

Iată implementarea corectă:

i = 0;
while ( i < n && v[i] != e )
  i++;
if ( i < n ) {
  n--;
  for ( ; i < n; i++ )
    v[i] = v[i+1];
}

Răsturnare vector

Se dă un vector v de n elemente. Inversați poziția elementelor în vector. Avem mai multe soluții posibile, una foarte simplă este să folosim doi indici, unul care crește și unul care descrește. Vom interschimba elementele celor doi indici. Vom repeta acest lucru pînă ce indicii se întîlnesc.

// avem vectorul v de n elemente, vrem sa il rasturnam
i = 0;
j = n – 1;
while ( i < j ) {
  aux = v[i];
  v[i] = v[j];
  v[j] = aux;
  i++;
  j--;
}

Rotire vector

Se dă un vector v de n elemente. Să se rotească vectorul cu o poziție către început cu o poziție. De exemplu [1, 6, 2, 7, 4, 3, 2] se va transforma în [6, 2, 7, 4, 3, 2, 1].

// avem vectorul v de n elemente, vrem sa il rotim la stinga cu o pozitie
aux = v[0];
for ( i = 1; i < n; i++ )
  v[i-1] = v[i];
v[n-1] = aux;

Mutare zerouri la coadă

Se dă un vector v de n elemente. Să se modifice ordinea elementelor în vector astfel încît toate elementele zero să fie la coada vectorului. Celelalte elemente nu trebuie să își păstreze ordinea originală (pot fi în orice ordine). O soluție posibilă este să mergem cu doi indici, unul crescător și unul descrescător. Cel crescător avansează pînă ce găsește un zero. Apoi interschimbă cu celălalt indice, pe care îl scade.

// avem vectorul v de n elemente, vrem sa mutăm zerourile la coada
i = 0;
j = n – 1;
while ( i < j ) {
  if ( v[i] == 0 ) { // daca avem un zero pe pozitia i
    v[i] = v[j];     // il trecem la coada, interschimbind cu pozitia j
    v[j] = 0;
    j--;             // deoarece pe pozitia j avem un zero, putem sa scadem j
  } else
    i++;             // daca avem nonzero pe pozitia i putem avansa i
}

Vector mulțime

Se dă un vector v de n elemente. Să se transforme într-un vector mulțime. Cu alte cuvinte, să se elimine duplicatele din vector. Un vector mulțime este un vector în care orice element apare o singură dată.

Avem mai multe soluții posibile. O primă soluție se bazează pe vectori de frecvență. Putem construi un vector de apariții ale elementelor din v. Apoi vom colecta elementele din vectorul de apariții înapoi in v. Această soluție funcționează pentru valori relativ mici ale elementelor din v.

Dacă valorile din v sînt prea mari pentru a folosi un vector de frecvență, atunci putem să verificăm fiecare element din vector și să îl copiem în alt vector, w, numai dacă el nu apare deja în vectorul w. Iată această soluție:

// avem vectorul v de n elemente, vrem sa il transformam in vector multime
m = 0; // numarul de elemente al vectorului w
for ( i = 0; i < n; i++ ) { // fiecare element din v va fi cautat in w
  j = 0;
  while ( j < m && w[j] != v[i] )
    j++;
  if ( j == m ) { // daca elementul v[i] nu exista in vectorul w, il adaugam
    w[m] = v[i];
    m++;
  }
}

Observație importantă: vectorul w are întotdeauna lungime mai mică sau cel mult egală cu vectorul v.

De aceea putem să nu folosim un vector diferit w, ci să lucrăm chiar pe vectorul v! Codul este identic cu cel de mai sus, înlocuind w cu v:

// avem vectorul v de n elemente, vrem sa il transformam in vector multime
m = 0; // numarul de elemente al vectorului multime
for ( i = 0; i < n; i++ ) { // fiecare element din v va fi cautat in multime
  j = 0;
  while ( j < m && v[j] != v[i] )
    j++;
  if ( j == m ) { // daca elementul v[i] nu exista in multime, il adaugam
    v[m] = v[i];
    m++;
  }
}
// in final vectorul v de lungime m contine multimea vectorului original

Căutare subvector în vector

Dați doi vectori, p (vectorul de căutat) și v (vectorul în care se caută) să se spună de cîte ori apare vectorul p în v. De exemplu dacă p = [1, 2, 1] și v = [1, 2, 1, 2, 1, 3, 1, 2, 1] atunci p apare de 3 ori in v.

Să observăm că aparițiile vectorului p în vectorul v pot fi suprapuse, ca în exemplul de mai sus. Un algoritm direct este să încercăm toate pozițiile de suprapunere ale vectorului p peste vectorul v și să testăm dacă toate elementele din p se potrivesc cu cele din v:

   1, 2, 1, 2, 1, 3, 1, 2, 1
0: 1, 2, 1
1:    1, 2, 1
2:       1, 2, 1
3:          1, 2, 1
4:             1, 2, 1
5:                1, 2, 1
6:                   1, 2, 1

Suprapunînd vectorul p peste v observăm că avem potriviri la pozițiile 0, 2 și 6. Iată programul pentru această metodă:

// avem vectorul v de n elemente si vectorul de cautat p, de m elemente
nr = 0;                                // numarul de aparitii este initial zero
for ( poz = 0; poz < n – m; poz++ ) {   // pentru fiecare pozitie posibila
  i = 0;
  while ( i < m && p[i] == v[poz + i] ) // ne oprim la prima inegalitate
    i++;
  if ( i == m )                         // daca toate elementele au fost egale
    nr++;                               // am mai gasit o aparitie a lui p in v
}
// acum nr contine numarul de aparitii ale lui p in v

Vom vedea în anii următori că există și algoritmi mai eficienți pentru rezolvarea acestei probleme.

Comparație vectori

Dați doi vectori de caractere să se spună care este ordinea lor lexicografică. Cu alte cuvinte, ordinea în care vor apărea cele două cuvinte în dicționar.

Un vector v1 este lexicografic mai mic decît alt vector v2 dacă v1 și v2 sînt egale de la 0 la i-1, iar poziția i este fie în afara vectorului v1, fie v1[i] < v2[i]. Vom compara elementele vectorilor pe aceleași poziții cîtă vreme sînt egale, oprindu-ne la prima diferență, sau cînd unul din vectori se termină. Acolo vom decide care din vectori este mai mic.

Iată programul:

// avem vectorii v1 de n1 elemente si v2 de n2 elemente
i = 0;
while ( i < n1 && i < n2 && v1[i] == v2[i] ) // cita vreme avem egalitate
  i++;                                       // avansam i
// pentru ca v1 sa fie primul in ordine lexicografica trebuie ca
// fie i sa fi depasit ultimul element din v1, fie ca v1[i] < v2[i]
// pentru a doua conditie e nevoie ca v2 sa aiba ceva pe pozitia i
if ( i == n1 || (i < n2 && v1[i] < v2[i]) )
  m = 0;
else
  m = 1;

Rotire multiplă de vector *

Se dă un vector v de n elemente și un număr k. Să se rotească vectorul cu o poziție către început cu k poziții. De exemplu, pentru k=3 [1, 6, 2, 7, 4, 3, 2] se va transforma în [7, 4, 3, 2, 1, 6, 2].

O soluție ar putea fi să rotim vectorul cîte o poziție de k ori. Această soluție face multe deplasări, respectiv k∙n. Un algoritm mai bun este următorul:

Răstoarnă vectorul v.
Răstoarnă subvectorul v[0..n-k-1]
Răstoarnă subvectorul v[n-k..n-1]

De ce funcționează acest algoritm?

Care este numărul de deplasări ale acestui algoritm? Demonstrați că este 3∙n.

Tema

Varianta 2: Mutare zerouri la coada

Mutarea zerourilor la coada, pastrand ordinea aparitiilor valorilor ( Compactarea vectorului )

Probleme de revizuit

Partea a I-a

1) Probleme cu secvente

( recaptulati lucrul cu caractere din lectia: http://algopedia.ro/wiki/index.php/Clasa_a_V-a_lec%C8%9Bia_18_-_9_dec_2014 )

2) Probleme cu vectori caracteristici

http://varena.ro/problema/comune ati avut-o ca tema in tema1. Acum o puteti rezolva cu vectori caracteristici
http://varena.ro/problema/culori

Partea a II-a

3) Vectori; Operatii pe vectori

http://varena.ro/problema/compus

Analiza complexitatii

Analizati complexitatea acestui algoritm si gasiti cea mai buna solutie de rezolvare:

https://www.codechef.com/problems/spalnum

Clasa a VI-a lecția 2: Difference between revisions