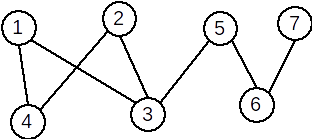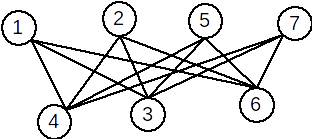Clasa a XI-a lecția 16

Note de curs: Isabela Coman

Graf Bipartit

Definiţie: Un graf G=(X, U) se numește graf bipartit dacă există două mulţimi nevide A și B astfel încât X=A ∪ B, A ∩ B = ∅ şi orice muchie u a lui G are o extremitate în A iar cealaltă în B. Mulţimile A şi B formează o partiţie a lui X.

Exemplu: Graful următor este bipartit. A={1,2,5,7} și B={3,4,6}.

Observatii:

• orice arbore este bipartit
• nu orice graf bipartit eate arbore.

Definiție: Un graf bipartit G=(X,U) se numește bipartit complet dacă pentru oricare două vârfuri x∈A și y∈B, există în graf muchia (x,y); adică (x,y)∈U.

Exemplu: Graful următor este bipartit complet.

Verificarea unui graf bipartit

Putem verifica daca un graf e bipartit in 2 moduri:

• un graf e bipartit daca putem colora nodurile cu 2 culori, astfel incat fiecare muchie sa aiba capete de culori diferite
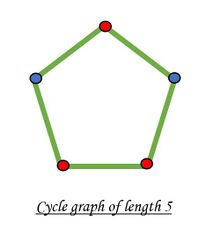
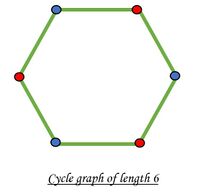
• un graf e bipartit daca nu contine cicluri de lungime para;

Bipartit1

Vom Utiliza metoda backtracking pentru a genera toate modalitatile de partitionare a celor n noduri. Vom folosi o stiva pentru a construi o solutie de dimensiune n. Pe stiva vom putea pun doar valori din multimea {1,2}. validarea unei solutii partiale consta in validarea unei valori noi adaugate pe nivelul curent k. Aceasta trebuie sa indeplineasca urmatoarea conditie:

• culoarea nodului k ( 1 sau 2 ) trebuie sa fie diferita de culorile vecinilos sai deja colorati.

#include <fstream>
#include <iostream>

using namespace std ;

ifstream fin ( "bipartit1.in" ) ;
ofstream fout ( "bipartit1.out" ) ;

int a[102][102], st[102];
int n, m;
int sol = 0 ;

void afisare (){
  if ( sol ){
    fout << "DA\n" ;
    for ( int i = 1 ; i <= n ; i++ )
      if ( st[i] == 1 )
        fout << i << " " ;
    fout << "\n" ;
    for ( int i = 1 ; i <= n ; i++ )
      if ( st[i] == 2 )
          fout << i << " " ;
  }
  else
    fout << "NU";
}
// e valida colorarea nodului k daca vecinii sai deja colorati au luloare diferita de el
int valid ( int k ){
  for ( int i = 1 ; i < k ; i++ )
    if ( st[i] == st[k] && a[i][k] == 1 )
      return 0;
 return 1;
}

void back ( int k ){
  if ( k == n + 1 ){
    sol++;
    return;
  }
  for ( int i = 1 ; i <= 2 && !sol ; i++ ){
     st[k] = i ;
     if ( valid ( k ) )
       back ( k + 1 ) ;
  }
}
int main (){
  fin >> n >> m ;
  for ( int i = 0; i < m ; i++ ){
    int x , y ;
    fin >> x >> y;
    a[x][y] = a[y][x] = 1 ;
  }
  back ( 1 ) ;
  afisare();
 return 0 ;
}

Folosirea BFS

bipartit1mare

Complexitatea de timp e aceeasi cu a algoritmului BFS. In implementarea de mai jos, unde parcugem vecinii memorati intr-o matrice de adiacenta vom avea complexitatea O(n^2) unde n e numarul de noduri. Complexitatea deriva din faptul ca pentru fiecare nod i din multimea celor n, parcurg toatea nodurile de la 1 la n pentru a verifica care noduri sunt vecine cu nodul i. Daca vom reprezenta graful folosind liste de adiacenta vom avea complexitate O(n+2m), unde n e numarul de noduri iar m numarul de muchii. In listele de adiacenta, parcurgem doar nodurile vecine asociate fiecarui nod. Vom avea 2m vecinatati memorate ( o muchia intre x si y este marcata si in lista lui x si in lista lui y).

#include <fstream>
#include <iostream>
using namespace std;
ifstream fin("bipartit1.in");
ofstream fout("bipartit1.out");

int n, m, i, j, x;
int a[1001][1001];
int c[1001];          // coada in care tin nodurile in ordinea vizitarii lor
int cul[1001];        // marchez daca am vizitat un nod; cand il vizitez il colorez cu 1 si -1

bool BFS( int start, int culoare ){                             // pornim parcurgerea de la un nod dat
  int i = 1;
  int vf = 0;
  cul[start] = culoare; //**                   // marchez ca vizitat nodul start
  c[++vf] = start;                             // punem in coada nodul de la care pornim
  while( i <= vf ){                            // cata vreme mai am elemente in coada
    int nod = c[i];                            // nodul curent
    //out << nod << " ";                       // afisez nodul curent
    for(int vecin = 1; vecin <= n; vecin++ )   // parcurg toti vecinii nodului curent
      if( a[nod][vecin] == 1 )
         if( cul[vecin] == 0 ){                // daca nu e colorat
            cul[vecin] = -cul[nod]; //**       // colorez diferit fata de nod
            c[++vf] = vecin;                   // ii pun in coada
         }
      else if( cul[vecin] == cul[nod] ) //**   // daca am dat de un vexin deja colorat cu aceeasi culoare cu nod
        return 0;                              // graful nu e bipartit
    i++;                                       // trec la urmatorul element din coada
  }
  return 1;
}

int main(){
  fin >> n >> m ;
  for( int l = 1; l <= m; l++ ){
    fin >> i >> j;
    a[i][j] = a[j][i] = 1;
  }
  int p = 1;                    
  for( int i = 1; i <= n; i++ )
    if ( cul[i] == 0 && p )
      p = (p && BFS( i, 1 ));         // apelam bfs pentru fiecare componenta conexa
  if( p ){                            // daca toate componentele au putut fi colorate
    fout << "DA\n";                   // graful e bipartit
    for( int i = 1; i <= n; i++ )     // afisam nodurile colorate cu 1 ( prima multime )
      if ( cul[i] == 1 )
        fout << i << " ";
    fout << "\n";
    for( int i = 1; i <= n; i++ )     // afisam nodurile colorate cu -1 
      if ( cul[i] == -1 )
        fout << i << " ";
  }
  else
    fout << "NU";
  return 0;
}

Folosirea DFS

bipartit1mare

#include <fstream>
#include <iostream>
using namespace std;
ifstream fin("bipartit1mare.in");
ofstream fout("bipartit1mare.out");

int n, m, i, j;
int a[1001][1001];
int cul[1001];        // marchez daca am vizitat un nod; cand il vizitez il colorez cu 1 si -1
int ok = 1;
void dfs( int nod, int culoare ){
  //out << nod << " ";                    // afisam nodul curent
  cul[nod] = culoare;                     // marcam nodul curent ca fiind vizitat, colorat
  for ( int i = 1; i <= n; i++ )          // parcurgem toti vecinii nodului curent
      if (a[nod][i] == 1 ){
        if(cul[i] == 0 )                  // daca nodul nu este vizitat
          dfs( i, -culoare );             // il colorez complementar nodului curent
        else
          if( cul[nod] == cul[i] )        // daca a mai fost vizitat, verific sa nu fie colorat la fel ca nodu lcurent
            ok = 0;                       // in acest caz graful nu e biparti
      }
}

int main(){
  fin >> n >> m ;
  for( int l = 1; l <= m; l++ ){
    fin >> i >> j;
    a[i][j] = a[j][i] = 1;
  }
  int p = 1;
  for( int i = 1; i <= n; i++ )
    if ( cul[i] == 0 ){
        ok = 1;
        dfs( i, 1 );
        p = ( p && ok );
    }

  if( p ){                            // daca toate componentele au putut fi colorate
    fout << "DA\n";                   // graful e bipartit
    for( int i = 1; i <= n; i++ )     // afisam nodurile colorate cu 1 ( prima multime )
      if ( cul[i] == 1 )
        fout << i << " ";
    fout << "\n";
    for( int i = 1; i <= n; i++ )     // afisam nodurile colorate cu -1
      if ( cul[i] == -1 )
        fout << i << " ";
  }
  else
    fout << "NU";
  return 0;
}

Tema

usor

• Bipartit2

medie

• java
• senat

grea

• album