Clasa a XI-a lecția 15: Difference between revisions
(No difference)
|
Latest revision as of 11:19, 7 February 2020
BFS
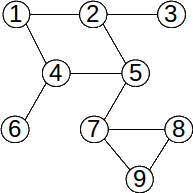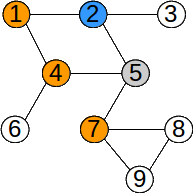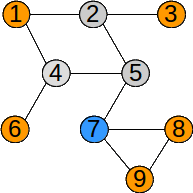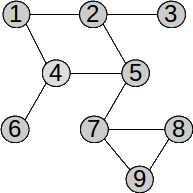
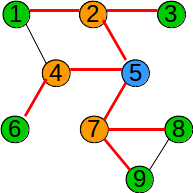
Se parcurge vârful de start, apoi vecinii acestuia, apoi vecinii nevizitați ai acestora, etc, până când sunt vizitate toate vârfurile accesibile. Practic, pentru a stabili ordinea de vizitare se folosește o coadă, iar pentru a stabili dacă un vârf a fost sau nu vizitat se foloseşte un vector caracteristic. Algoritmul este: adaugăm în coadă vârful inițial și îl vizităm cât timp coada este nevidă extragem un element din coadă determinăm vecinii nevizitați ai vârfului extras, îi vizităm și îi adăugăm în coadă eliminăm elementul din coadă Observație Dacă graful nu este conex, în urma parcurgerii nu se vor vizita toate vârfurile.
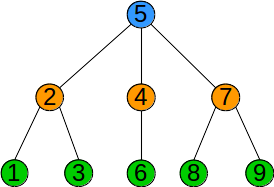
Vârfurile grafului au fost parcurse în ordinea: 5 2 4 7 1 3 6 8 9.\ În urma parcurgerii în latime, muchiile folosite pentru parcurgere formează un arbore. Acest arbore este graf parțial al grafului dat (dacă graful este conex), și se numește arbore parțial de parcurgere. Pentru graful de mai sus, arborele de parcurgere pornind din vârful 5 este:
Acest arbore poate fi considerat arbore cu rădăcină, aceasta fiind chiar vârful de start, 5.
În acest caz, odată cu parcurgerea se poate construi și vectorul de “tați” t[] al arborelui. În acest exemplu el este:
k 1 2 3 4 5 6 7 8 9 t[k] 2 5 2 5 0 4 5 7 7
Din vectorul de tați al unui arbore se poate determina ușor pentru un vârf oarecare un lanț de la acel vârf la rădăcina arborelui. Arborii obținuți în urma parcurgerii în lățime au proprietatea că lanțul de la vârful de pornire la oricare vârf accesibil din graf obținut din arborele de parcurgere are lungime minimă.
BFS Nerecursiv
void BFS( nod de start ){
marcam ca vizitat nodul de start
punem nodul de start in coada
while( avem elem in coada ){
parcurg toti vecinii primului nod din coada si pentru fiecare vecin nevizitat al acestuia
il marchez ca vizitat
il pun in coada
sterg din coada nodul curent/trec la urm element din coada
}
}BFS Recursiv
Inainte de a apela functia, vom pune nodul de start in coada, marcandu-l ca vizitat
void BFS( ){
if (coada nu e vida)
extrag primul nod din coada si il tiparesc
parcurg toti vecinii acestuia si pentru fiecare vecin nevizitat
il marchez ca vizitat
il pun in coada
scot din coada primul element
reapelez functia
}BFS Nerecursiv - pe matrice de adiacenta, implementare coada pe vector
#include <fstream>
using namespace std;
ifstream in("BFS.in");
ofstream out("BFS.out");
int n, m, i, j, x;
int a[1001][1001];
int c[1001]; // coada in care tin nodurile in ordinea vizitarii lor
int v[1001]; // vector de frecventa in care marchez daca am vizitat un nod
void BFS( int start ){ // pornim parcurgerea de la un nod dat
int i = 1;
int vf = 0;
v[start] = 1; // marchez ca vizitat nodul start
c[++vf] = start; // punem in coada nodul de la care pornim
while( i <= vf ){ // cata vreme mai am elemente in coada
int nod = c[i]; // nodul curent
out << nod << " "; // afisez nodul curent
for(int vecin = 1; vecin <= n; vecin++ ) // parcurg toti vecinii nodului curent
if( a[nod][vecin] == 1 && v[vecin] == 0 ){ // daca vecinii nu au fost vizitati
v[vecin] = 1; // mstchez vecinul ca vizitat
c[++vf] = vecin; // ii pun in coada
}
i++; // trec la urmatorul element din coada
}
}
int main(){
in >> n >> m >> x;
for( int l = 1; l <= m; l++ ){
in >> i >> j;
a[i][j] = a[j][i] = 1;
}
BFS( x );
return 0;
}BFS Nerecursiv - reprezentare cu matrice de adiacenta, implementare coada din queue
#include <fstream>
#include <queue>
using namespace std;
ifstream in( "BFS.in" );
ofstream out( "BFS.out" );
int mat[101][101], n;
bool viz[101]; // vectorul in care marcam daca un nod a fost vizitat sau nu
queue<int> q; // coada in care pun nodurile in ordinea vizitarii
void bfs( int start ){
q.push(start); // punem notul x in stiva lis
viz[start] = 1; // marcam ca vizitat nodul x in strun vect de frecv
out << start; // facem afisarea pe masura ce parcurgem
while( q.size() ) { // cata vreme am elem in coada
for( int i = 1; i <= n; i++ ){ // parcurg toti vecinii si ii pun in coada pe cei nevizitati
int nod = q.front();
if( mat[nod][i] && !viz[i] ){ // pe poz 0 in coada voi avea tot timpul elementul curent
q.push(i); // pun vecinul in coada
out << " " << i; // afizez vecinul
viz[i] = 1; // il marchez ca vizitat
}
}
q.pop(); // scot din coada modul pe care tocmai l-am afisat si caruia i-am parcurs toti vecinii
}
}
int main(){
int m, i, a, b, start;
in >> n >> m >> start; // start = nodul de la care incepem parcurgerea bfs
for( i = 0; i < m; i++ ) {
in >> a >> b;
mat[a][b] = 1;
mat[b][a] = 1;
}
bfs( start );
return 0;
}BFS Rerecursiv - reprezentare cu matrice de adiacenta
Varianta 1 de implementare cu coada pe vector
// BFS recursiv, matrice de adiacenta
#include <fstream>
using namespace std;
ifstream in ("bfs.in");
ofstream out ("bfs.out");
int a[102][102], n, sf, k; // sf - sfarsitul cozii, k -nodul curent
bool viz[102]; // pentru fiecare nod marcam daca a fost vizitat
int c[102]; // coada care retine nodurile in ordinea vizitarii
void bfs(){
if ( k <= sf ){ // daca coada nu e vida
int nod = c[k]; // extrag primul element si il tiparesc
out << nod << " "; // afisez elem
for (int i = 1 ; i <= n; i++) // pun in coada toti vecinii nevizitati ai lui nod
if ( a[nod][i] == 1 && viz[i] == 0 ){
c[++sf]= i;
viz[i] = 1;
}
k++;
bfs();
}
}
int main(){
int m, start;
in >> n >> m >> start;
for ( int i = 1; i <= m; i++ ) {
int x, y;
in >> x >> y;
a[x][y] = a[y][x] = 1;
}
// incep parcurgerea grafului de la nodul start
c[1] = start; // pun nodul start in coada
viz[start] = 1; // il marchez ca l-am vizitat
k = sf = 1; // k - nodul pe care ma gasesc, sf sfarsitul cozii in care pun nodurile ce urmeaza a fi vizitate
bfs();
return 0;
}Varianta de implementare cu coada din queue
// folosind coada, recursiv
#include <fstream>
#include <queue>
using namespace std;
ifstream in ("BFS.in");
ofstream out ("BFS.out");
queue<int> q; // definim q o coada de int-uri
int a[102][102], n;
bool viz[102]; // pentru fiecare nod marcam daca a fost vizitat
void bfs(){
if ( !q.empty() ){ // daca coada nu e vida
int nod = q.front(); // extrag primul element si il tiparesc
out << nod << " ";
for (int i = 1 ; i <= n; i++){ // pun in coada toti vecinii mevizitati primului element din coada
if ( a[nod][i] == 1 && viz[i] == 0 ){
q.push(i);
viz[i] = 1;
}
}
q.pop();
bfs();
}
}
int main(){
int m, start;
in >> n >> m >> start;
for ( int i = 1; i <= m; i++ ) {
int x, y;
in >> x >> y;
a[x][y] = a[y][x] = 1;
}
q.push(start);
viz[start] = 1;
bfs();
return 0;
}
BFS Rerecursiv - reprezentare cu matrice de adiacenta, implementare coada din queue
// folosind coada, recursiv
#include <fstream>
#include <queue>
using namespace std;
ifstream in ("BFS.in");
ofstream out ("BFS.out");
queue<int> q; // definim q o coada de int-uri
int a[102][102], n;
bool viz[102]; // pentru fiecare nod marcam daca a fost vizitat
void bfs(){
if ( !q.empty() ){ // daca coada nu e vida
int nod = q.front(); // extrag primul element si il tiparesc
out << nod << " ";
for (int i = 1 ; i <= n; i++){ // pun in coada toti vecinii mevizitati primului element din coada
if ( a[nod][i] == 1 && viz[i] == 0 ){
q.push(i);
viz[i] = 1;
}
}
q.pop();
bfs();
}
}
int main(){
int m, start;
in >> n >> m >> start;
for ( int i = 1; i <= m; i++ ) {
int x, y;
in >> x >> y;
a[x][y] = a[y][x] = 1;
}
q.push(start);
viz[start] = 1;
bfs();
return 0;
}TEMA BFS
Tema Teorie + Laborator
Implementare BFS
- BFS PBINFO - TEORIE
- BFS INFOARENA - TEORIE
Tema Optionala
recapitulare BFS pe matrice ( LEE )
usor
- https://www.pbinfo.ro/?pagina=probleme&id=2165 graf1 OJI 2006, Clasele XI-XII
- https://www.pbinfo.ro/?pagina=probleme&id=1021 cartite OJI 2014, Clasele XI-XII
mediu
- https://www.infoarena.ro/problema/reinvent - ONI 2009, clasele 11-12
- https://www.infoarena.ro/problema/amici2 - ONI 2013, clasele 11-12
- https://www.infoarena.ro/problema/markon - Concursul National Urmasii lui Moisil 2012, clasele 11-12
- https://www.infoarena.ro/problema/banana - ONI 2002 (??? dificultate )
greu
- https://www.infoarena.ro/problema/atac2 - ONI 2008 clasele 11-12 BFS/Belman/Cuplaj de cos minim
- https://codeforces.com/problemset/problem/398/C constructive algorithms
mai multe probleme [=47 aici]:
Tema Rezolvari
Lant minim de la p la q - afisare drum Se dă lista muchiilor unui graf neorientat și două vârfuri p q. Să se determine cel mai scurt lanț cu extremitățile p q.
lantminim.in 6 2 6 1 2 1 3 1 4 3 4 4 5 4 6 5 6
lantminim.out 4 2 1 4 6
Observatie: Lungimea lantului intre 2 1 4 6 este de fapt 3. Prin definitie, lungimea unui lant este numarul muchiilor, nu numarul de noduri componente ale lantului. Problema specifica insa ca se doreste a se afisa numarul de noduri din lantul minim, ci nu lungimea lantului.
Rezolvare: Vom parcurge in latime graful, pornind de la nodul p. Pe masura ce vom vizita nodurile:
- vom memora pentru fiecare nod distanta de la p la acestea, intr-un vector dist. Astfel ca la final dist[q] va retine distanta de la p la q.
- vom memora pentru fiecare nod, nodul prin care s-a ajuns la acesta, adica predecesorul lui, sau cum l-am denumit aici tatal. Acest vector de tati ne ajuta sa reconstituim drumul din aproape in aproape pornind de la nodul q, pana la nodul de pornire, pentru care tatal e 0.
#include <fstream>
using namespace std;
ifstream fin("lantminim.in");
ofstream fout("lantminim.out");
/// pt p = 2 si q = 6 si muchiile : 1 2, 1 3, 1 4,3 4,4 5,4 6,5 6
/// nod: 1 2 3 4 5 6 7
/// tati: 2 0 1 4 // tatal lui 6 e 4, al lui 4 e 1, al lui 1 e 2, al lui 2 e 0 ( de la el am pornit deci ne oprim)
int n, m, i, j, p, q;
int a[101][101];
int coada[101]; // coada in care tin nodurile in ordinea vizitarii lor
int dist[101]; // dinst de la nodul de start pana la nodul curent
int tata[101]; // vector de frecventa in care marchez daca am vizitat un nod
void tipar( int q ){ // tipareste nodurile prin care am ajuns la q folosindu-ne de vect de tati
if( q ){ // daca q e 0 ne oprim,
tipar ( tata[q] ); // tiparesc intai tatal lui q si apoi q
fout << q << " ";
}
}
void BFS( int start ){ // pornim parcurgerea de la un nod dat
int k = 1;
int vf = 0;
dist[start] = 1; // marchez ca vizitat nodul start in vectorul in care itn distantele
tata[start] = 0;
coada[++vf] = start; // punem in coada nodul de la care pornim
while( k <= vf ){ // cata vreme mai am elemente in coada
int nod = coada[k]; // nodul curent
//fout << nod << " "; // afisez nodul curent
for(int i = 1; i <= n; i++ ) // parcurg toti vecinii nodului curent
if( a[nod][i] == 1 && dist[i] == 0 ){ // daca vecinii nu au fost vizitati (nu le-am marcat dist pana la p
coada[++vf] = i; // ii pun in coada
dist[i] = dist[nod] + 1; // dist de la start pana la el, e dist de la nod pana la start + 1
tata[i] = nod;
}
k++; // trec la urmatorul element din coada
}
}
int main(){
fin >> n >> p >> q;
while( fin >> i >> j ){
a[i][j] = a[j][i] = 1;
}
BFS( p );
fout << dist[q] << "\n"; // tiparim dist de la p la q memorata in vect dist
tipar( q ); // tiparim nodurile prin care am trecut ca sa ajung la q, folosindu-ne de vect de tati
return 0;
}