Clasa a 7-a Lecția 24: Programare dinamică (1)

Înregistrare video lecție

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Conceptul de programare dinamică

Introducere

Wikipedia definește programarea dinamică drept o metodă pentru rezolvarea unor probleme complexe prin descompunerea lor în subprobleme mai simple. Se poate aplica problemelor care prezintă proprietățile de suprapunere a subproblemelor și de substructură optimală. Atunci când se poate aplica, metoda ia mult mai puțin timp decât alte soluții naive.

Drumul cel mai scurt între două orașe poate fi rezolvat cu programare dinamică

Substructura optimală înseamnă că soluția unei problemei de optimizare date poate fi obținută prin combinarea unor soluții optimale ale subproblemelor. Ca atare, primul pas către găsirea unei rezolvări prin această metodă este verificarea dacă problema are proprietatea substructurii optimale.

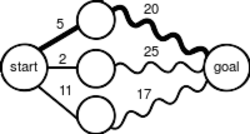
Drumul cel mai scurt între două orașe poate fi rezolvat cu programare dinamică

Astfel de substructuri optimale sunt în mod uzual descrise prin recurență. De exemplu, date niște orașe și distanțele între ele, drumul cel mai scurt de la orașul u la orașul v are proprietatea de substructură optimală: să luăm orice oraș intermediar w pe drumul cel mai scurt, d. Dacă d este cu adevărat drumul cel mai scurt, atunci drumul d1 de la u la w și d2 de la w la v sunt cu adevărat cele mai scurte drumuri între orașele corespunzătoare. Dacă drumul de la u la w nu ar fi cel mai scurt posibil ar însemna că am avea un alt drum mai scurt, ceea ce ar duce la un drum total d, de la u la v, mai scurt decât cel original. Așadar, putem formula soluția problemei găsirii celui mai scurt drum într-o manieră recursivă, ceea ce fac algoritmii Bellman-Ford și Floyd-Warshall.

Suprapunerea subproblemelor înseamnă că ele nu sunt independente, adică subproblemele au în comun alte subprobleme. Nu vom insista pe această proprietate decât atât cât să menționăm că dacă subproblemele nu se suprapun dar prezintă substructură optimală atunci putem aplica tehnica de programare divide et impera (divide and conquer). De aceea quicksort și mergesort nu sunt clasificate ca probleme de programare dinamică.

Metodă

Când încercăm să rezolvăm o problemă de programare dinamică întrebarea crucială la care trebuie să răspundem este putem calcula soluția finală pe baza unor subprobleme care sunt la rândul lor optimale ? Pentru a răspunde la întrebare trebuie mai întâi să formulăm subproblemele. Dar pentru a formula subproblemele trebuie să avem în minte principiul substructurii optimale. Altfel s-ar putea să împărțim problema în subprobleme care nu au substructură optimală.

Să recapitulăm: pentru a putea răspunde la întrebarea dacă o problemă admite o soluție prin programare dinamică trebuie să aflăm dacă are substructură optimală. Dar pentru a afla dacă are substructură optimală trebuie să găsim subproblemele. Pe care încercăm să le găsim folosind programarea dinamică.

Nu cumva ne învârtim în cerc? Așa pare și așa și este, într-o oarecare măsură. Experiența este cea care ne învață cum să căutăm împărțirea în subprobleme astfel încât să obținem proprietatea de optimalitate. Tot experiența este cea care ne ajută să ne dăm seama rapid dacă împărțirea găsită are această proprietate sau nu.

Odată ce demonstrăm că o împărțire în subprobleme se bazează doar pe subprobleme optimale, restul decurge, de obicei, destul de simplu: găsim o formulă de recurență, apoi o implementăm de jos în sus (sau bottom-up), pornind de la cele mai mici probleme, către cele mai mari, până la soluția cerută.

În continuare vom lua câteva exemple.

Subsecvența crescătoare de lungime maximă

Această problemă cere să găsim o subsecvență a unei secvențe de numere în care elementele sunt în ordine crescătoare, iar subsecvența este de lungime maximă. Subsecvența nu este neapărat contiguă, nici unică.

Exemplu

În secvența

0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15

o secvență crescătoare de lungime maximă este

0, 2, 6, 9, 13, 15

Această secvență are lungime șase. Nu există nici o secvență crescătoare de lungime șapte. Cea mai lungă subsecvență crescătoare nu este unică. De exemplu

0, 4, 6, 9, 11, 15

este o altă subsecvență crescătoare de aceeași lungime, în secvența de intrare.

Soluție

Cum împărțim problema în subprobleme? Să încercăm astfel:

L[i] = lungimea celei mai lungi subsecvențe care începe la poziția i

Are această împărțire proprietatea de optimalitate? Să presupunem că avem o subsecvență optimală crescătoare care trece prin indicii

i1, i2, i3, …, ik

Astfel

L[i1] = k

Este secvența i₂, ..., i_k optimală? Cu alte cuvinte lungimea secvenței optime care începe la i₂ este k-1? Răspunsul este da, secvența care începe la i₂, anume i₂, ..., i_k este o secvență maximă, deoarece altfel am putea-o înlocui cu o secvență mai lungă, ceea ce ar duce la o subsecvență L[i₁] mai lungă decât cea inițială, care era optimală. Obținem o contradicție.

Următorul pas este să găsim relația de recurență:

L[i] = max(L[j]+1), j > i și V[j] ≥ V[i]

Următorul pas este să construim subproblemele bottom-up, de la problemele mai mici la cele mai mari. Pentru aceasta vom calcula vectorul L de la coadă la cap, căutând pentru fiecare element L[i] cel mai mare element L[j] de după el (j > i) astfel încât V[j] ≥ V[i].

Soluția problemei este maximul din vectorul L.

Exemplu

Să calculăm cea mai lungă secvență crescătoare în secvența:

0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15

Vom calcula lungimile secvențelor maximale de la coadă la cap: L[15], apoi L[14] și așa mai departe. Când ajungem la calculul lui L[6] avem următoarea situație:

Exemplu de calcul pentru elementul L[6] - cea mai lungă secvență crescătoare care începe la poziția 6.

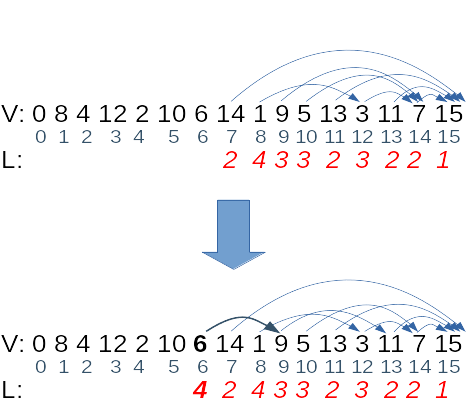
Pentru a calcula lungimea secvenței maximale care începe la poziția 6 vom căuta toate pozițiile mai mari (7, 8, 9, ...). Le vom lua în considerare doar pe acelea în care V[i] >= V[6]. Dintre ele vom alege poziția unde L[i] este maximă. Astfel vom găsi că V[9] = 9 și L[9] = 3. Vom avea, deci, o secvență de lungime 4. Ea este:

6, 9, 11, 15

Exemplu de calcul pentru elementul L[6] - cea mai lungă secvență crescătoare care începe la poziția 6.

Analiză

Acest algoritm are complexitate O(n²), unde n este lungimea secvenței. Memoria folosită este O(n).

Există și un algoritm mai rapid, de complexitate O(n log n), bazat pe căutare binară a valorilor de început.

Reconstrucția soluției

Putem reconstrui o subsecvență maximală folosind încă un vector, N[]. El memorează pentru fiecare indice i un alt indice j care urmează în secvență după j. Atunci când calculăm elementul curent, vom nota nu doar maximul găsit (plus unu) ci și poziția lui în vector, el fiind elementul următor în secvență.

Subșirul de sumă maximală

Această problemă cere să găsim un subșir de sumă maximă într-un șir de numere. Un subșir este contiguu.

Exemplu

Să considerăm șirul:

12, 14, 0, -4, 61, -39

subșirul de sumă maximală este:

12, 14, 0, -4, 61

și are sumă 83.

Soluție

Cum împărțim problema în subprobleme? Să încercăm astfel:

S[i] este suma maximală a unui șir care se termină la poziția i

Are această împărțire proprietatea de optimalitate?

Să presupunem că avem un subșir de sumă maximă și că el se află între indicii i și j. Cu alte cuvine suma maximală este

S[j] = V[i] + V[i+1] + ... + V[j-1] + V[j]

Are șirul care se termină în j-1, sumă maximală? Cu alte cuvinte este suma

S[j-1] = V[i] + V[i+1] + ... + V[j-1]

maximală?

Răspunsul este da, deoarece altfel am putea-o înlocui cu o sumă mai mare, ceea ce ar duce la o sumă mai mare decît cea inițială, care era optimală. Obținem o contradicție.

Următorul pas este să găsim relația de recurență. Observăm că pentru o poziție i avem două variante: fie continuăm secvența anterioară, care se termină în i-1, fie începem una nouă, care pornește în i. Vom continua secvența anterioară dacă adunând numărul curent obținem o sumă mai mare strict decât numărul curent. Altfel vom porni o sumă nouă. Relația de recurență este:

S[i] = max(V[i], S[i-1] + V[i])

Următorul pas este să construim subproblemele bottom-up, de la problemele mai mici la cele mai mari. Pentru aceasta vom calcula vectorul S calculând pentru fiecare element S[i] maximul dintre S[i-1] + V[i] și V[i]. Observăm că, în realitate, vom compara S[i-1] cu zero.

Soluția problemei este maximul din vectorul S.

Exemplu

Fie secvența anterioară:

12, 14, 0, -4, 61, -39

Vom calcula de la stânga la dreapta sumele maximale ce se termină la pozițiile respective:

V	12	14	0	-4	61	-39
S	12	26 = max(14, 12 + 14)	26 = max(0, 0 + 26)	22 = max(-4, -4 + 26)	83 = max(61, 61 + 22)	44 = max(-39, -39 + 83)

Analiză

Acest algoritm are complexitate O(n), unde n este lungimea șirului. Memoria folosită este O(1), deoarece nu avem nevoie să stocăm elementele, ci doar ultima sumă calculată.

Reconstrucția soluției

Putem ține minte șirul maximal ținând minte începutul și sfârșitul subșirului maximal atunci când îl găsim.

Soluții alternative

Această problemă poate fi rezolvată fără programare dinamică. Ne propunem același lucru, ca la pasul i să calculăm S[i] cu aceeași semnificație. Acest S[i] se poate calcula cu cunoștințe de nivel mic: sume parțiale. S[i] va fi suma unei secvențe de la k la i, cu k ≤ i. Deci, dacă vom calcula P[], sumele parțiale pe vector putem spune că S[i] = P[i] - P[k]. Să ne uităm puțin la această expresie: cine variază în ea? P[i] este constant, este suma elementelor până la i. Putem varia doar P[k]. Este evident că dorim să alegem un P[k] cât mai mic, nu?

Algoritmul este unul banal: calculează sume parțiale, avansând i. Suma minimă care se termină în i este suma parțială curentă minus suma parțială minimă din trecut. La fiecare avans actualizează suma parțială minimă cu cea curentă, dacă este cazul.

Acest algoritm are aceleași complexități ca cel cu programare dinamică. El este însă un algoritm mai flexibil de adaptat unor modificări, cum ar fi suma maximă de lungime cel puțin K sau suma maximă de lungime cel mult K.

Subșirul comun maximal al două șiruri

Această problemă cere să găsim lungimea unui subșir de lungime maximă (contiguu) inclus în două șiruri.

Exemplu

Date șirurile

ABABC

și

CBABA

un subșir maximal are lungime 3 și este

BAB

Soluție

Cum împărțim problema în subprobleme? Să observăm că deoarece subșirul maximal face parte din ambele șiruri el se va termina la o poziție i în șirul X și la o poziție j în șirul Y. Și atunci să încercăm astfel:

M[i][j] = lungimea celui mai lung subșir care se termină la poziția i în X și la poziția j în Y.

Are această împărțire proprietatea de optimalitate?

Să presupunem că avem un subșir optimal care se termină la pozițiile i, respectiv j. Atunci este subșirul M[i-1][j-1] la rândul lui optimal? Cu alte cuvinte subșirul mai scurt cu unu, care se termină la pozițiile anterioare în X, respectiv Y, este optimal? Da, el este optimal, caci altfel l-am putea înlocui cu un șir mai lung, care ar duce la o soluție mai bună, ceea ce ar însemna că soluția originală nu a fost optimă.

Următorul pas este să găsim relația de recurență:

$M[i][j]={\begin{cases}M[i-1][j-1]+1,&{\mbox{dacă }}X[i]=Y[j]\\0,&{\mbox{în caz contrar }}.\end{cases}}$

Următorul pas este să construim subproblemele bottom-up, de la problemele mai mici la cele mai mari. Pentru aceasta vom calcula matricea M pe linii, folosind formula de recurență.

Soluția problemei este maximul din matrice.

Exemplu

Pentru cele două șiruri de mai sus,

ABABC

și

CBABA

Vom calcula o matrice M[5][5] care arată astfel:

	C	B	A	B	A
A	0	0	1	0	1
B	0	1	0	2	0
A	0	0	2	0	3
B	0	1	0	3	0
C	1	0	0	0	0

Observăm că avem două subșiruri comune de lungime 3: ABA și BAB.

Analiză

Acest algoritm are complexitate O(m·n), unde m și n sunt lungimile șirurilor. Memoria folosită este, la prima vedere, O(m·n). În realitate, parcurgând matricea pe linii, nu avem nevoie să memorăm decât o linie din matrice pentru a calcula toate valorile. De aceea memoria necesară este O(min(m, n)).

Există și algoritmi mai eficienți bazați pe arbori sufix, despre care nu vom discuta aici.

Reconstrucția soluției

Cum facem să aflăm nu doar lungimea ci și care este șirul comun maximal și unde apare el în cele două șiruri?

Vom face calculul matricei noastre printr-o parcurgere pe linii. La fiecare pas ne vom întreba dacă elementul calculat (lungimea) este mai mare decât maximul curent. Dacă da, vom memora acel maxim împreună cu indicii i și j la care s-a obținut el.

La final vom avea poziția de start în primul șir ca fiind i - max + 1 și în al doilea șir ca fiind j - max + 1.

Subsecvența comună maximală a două șiruri

Această problemă cere să găsim lungimea unei subsecvențe de lungime maximă inclusă în două secvențe. Prin secvență înțelegem caractere în ordinea originală, nu neapărat consecutive ca poziție.

Exemplu

Date secvențele

X: ACDEGIKMPR
Y: CMEFPGHRK

o secvență maximală are lungime 4 și este

CEGK

o altă secvență maximală este

CMPR

Soluție

Cum împărțim problema în subprobleme? Să încercăm să o împărțim în mod similar cu subșirul comun maximal:

M[i][j] = lungimea celei mai lungi subsecvențe incluse în șirurile X[1..i] și Y[1..j]

Are această împărțire proprietatea de optimalitate?

Să presupunem că avem o secvență optimală a prefixelor care se termină la pozițiile i, respectiv j. Ea va trece prin anumite perechi (i_k, j_k), strict crescătoare, cu proprietatea că X[i_k] = Y[j_k]:

Si,j = (i1, j1) (i2, j2) ... (ik, jk)

cu proprietatea că:

Xi1Xi2... Xik-1Xik = Yj1Yj2... Yjk-1Yjk

Atunci este lungimea M[i_k-1][j_k-1] la rândul ei optimală? Cu alte cuvinte subsecvența mai scurtă cu unu, care se termină la poziția i_k-1 în X, respectiv poziția j_k-1 în Y, este optimală? Da, ea este optimală, căci altfel am putea-o înlocui cu o secvență mai lungă, care ar duce la o soluție mai bună, ceea ce ar însemna că soluția originală nu a fost optimă.

Următorul pas este să găsim relația de recurență:

$M[i][j]={\begin{cases}0,&{\mbox{dacă }}i=0{\mbox{ sau }}j=0\\M[i-1][j-1]+1,&{\mbox{dacă }}X[i]=Y[j]\\max(M[i-1][j],M[i][j-1])&{\mbox{dacă }}X[i]\neq Y[j].\end{cases}}$

Cum demonstrăm această relație de recurență? Avem două cazuri de demonstrat:

Egalitate

Prefixele X[1..i] și Y[1..j] se termină în același caracter. În acest caz o subsecvență maximală a celor două prefixe se poate obține selectând acel ultim caracter. Putem, deci exclude acel caracter și calcula subsecvența maximală în prefixele X[1..i-1] și Y[1..j-1]. La lungimea ei vom aduna unu.

Diferență

Prefixele X[1..i] și Y[1..j] se termină în caractere diferite. Să luăm cazul anterior, avem secvențele:

X: ACDEGIKMPR
Y: CMEFPGHRK

Avem iarăși două cazuri:

• Cazul 1: subsecvența optimă se termină în R. În acest caz ea nu se poate termina și în K. Deci putem elimina ultimul caracter din Y și calcula M[i][j-1].
• Cazul 2: subsecvența optimă nu se termină în R. În acest caz putem elimina acest R și calcula M[i-1][j].

Următorul pas este să construim subproblemele bottom-up, de la problemele mai mici la cele mai mari. Pentru aceasta vom calcula matricea M pe linii, folosind formula de recurență.

Soluția problemei este M[n][m].

Exemplu

Pentru cele două șiruri de mai sus,

ACDEGIKMPR

și

CMEFPGHRK

Vom calcula o matrice M[10][9] care arată astfel:

	C	M	E	F	P	G	H	R	K
A	0	0	0	0	0	0	0	0	0
C	1	1	1	1	1	1	1	1	1
D	1	1	1	1	1	1	1	1	1
E	1	1	2	2	2	2	2	2	2
G	1	1	2	2	2	3	3	3	3
I	1	1	2	2	2	3	3	3	3
K	1	1	2	2	2	3	3	3	4
M	1	2	2	2	2	3	3	3	4
P	1	2	2	2	3	3	3	3	4
R	1	2	2	2	3	3	3	4	4

Cea mai lungă secvență este de lungime 4, valoarea maximă ce apare în tabel.

Analiză

Acest algoritm are complexitate O(m · n), unde m și n sunt lungimile șirurilor. Memoria folosită este O(min(m,n)) dacă memorăm doar o linie din matrice. Dacă dorim să aflăm și o secvență maximală, nu doar lungimea ei, vom avea nevoie de memorie O(m · n), precum vom vedea mai jos.

Există un algoritm care reduce necesarul de memorie la O(min(m, n)).

Reconstrucția soluției

Dorim să aflăm nu doar lungimea, ci și o secvență maximală inclusă în ambele șiruri. Cum procedăm?

Observăm că literele ce fac parte din secvențele maximale se obțin acolo unde, în matrice, avem ramura doi de calcul, când literele de la pozițiile respective sunt egale.

Pentru a putea reconstrui soluția vom memora în fiecare căsuță, pe lângă lungimea maximă și direcția din care provine ea, adică din care am calculat acel maxim. Direcția poate fi spre stânga, spre în sus, sau în diagonală stânga-sus. Apoi vom porni din elementul M[m][n] și vom urma aceste direcții până ce ieșim din matrice. De fiecare dată când urmăm o diagonală reținem litera. Astfel, descoperirea secvenței se face în ordine inversă.

Tema 24

Să se rezolve următoarele probleme (program C trimis la NerdArena):

• Dreptunghiuri pentru subsecvența crescătoare maximală. Atenţie: puteți pica teste cu TLE, este în regulă.
• Subsecvența de sumă maximă
• Subșirul comun de lungime maximă
• Cel mai lung subșir comun

Accesează rezolvarea temei 24