Clasa VI/VII/VIII lecția 8 - 23 oct 2012

Lecție

Matrice, continuare

• Parcurgerea pe diagonale. N-am văzut la nimeni citirea corectă a matricei pătrate de caractere. Iată o variantă clasică. Citim prima linie pentru a determina dimensiunea n, iar apoi citim restul de linii în mod normal, știind dimensiunea:

  #include <stdio.h>
  
  int main() {
    FILE *fin, *fout;
    int i, j, n;
    char c, m[100][100];
  
    fin = fopen( "diagonale.in", "r" );
    // citim prima linie si determinam n
    n = 0;
    m[0][n] = fgetc( fin );
    while( m[0][n] != '\n' )  {
      n++;
      m[0][n] = fgetc( fin );
    }
    // citim restul liniilor (1 la n-1) stiind dimensiunea n
    for ( i  = 1; i < n; i++ ) {
      for ( j = 0; j < n; j++ )
        m[i][j] = fgetc( fin );
      fgetc( fin ); // scapa de sfirsitul de linie '\n'
    }
    // am terminat citirea, urmeaza restul programului
    return 0;
  }

• Rezolvarea propriu zisă a problemei. Iată o variantă, afișarea primei linii:

    // ... după citire
    // afisam diagonalele de sub diagonala principala, inclusiv
    fout = fopen( "diagonale.out", "w" );
    for ( i = n – 1; i >= 0; i-- )  // pentru fiecare linie incepind de jos in sus
      for ( j = 0; j < n - i; j++ ) // pentru fiecare coloana, pornind de la 0
        fputc( m[i + j][j], fout );
    // afisam diagonalele de deasupra diagonalei principale
    for ( j = 1; j < n; j++ )       // pentru fiecare coloana incepind cu 1
      for ( i = 0; i < n - j; i++ ) // pentru fiecare linie de la 0 la j – 1
        fputc( m[i][i + j], fout );
    fputc ( '\n', fout );
    // am terminat de afisat prima linie, urmeaza afisarea liniei 2

• Rezolvare zoom x2. Să presupunem că avem matricea inițială a de dimensiune n și matricea finală b de dimensiune 2*n. Am vorbit despre doua variante:
  • Varianta 1: parcurgem matricea ințială a și o generăm pe cea finală b:

      for ( i = 0; i < n; i++ )
        for ( j = 0; j < n; j++ )
          b[2*i][2*j] =
            b[2*i+1][2*j] =
            b[2*i][2*j+1] =
            b[2*i+1][2*j+1] = a[i][j];

  • Varianta 2: parcurgem matricea ințială a și o generăm pe cea finală b:

      for ( i = 0; i < 2*n; i++ )
        for ( j = 0; j < 2*n; j++ )
          b[i][j] = a[i/2][j/2];

  • Am comparat cele două variante. Am vorbit despre faptul că împărțirea este mai lentă decît înmulțirea și despre faptul că înmulțirea și împărțirea cu doi se pot optimiza la shift.
• Rezolvări teme din urmă:
  • cartier punctul c: dat un vector v de n numere (înălțimi) să se găsească două numere la distanță maximă în vector astfel încît ele să nu fie prime între ele. Rezolvare aici: [1]
  • medalion punctul b: dată o spirală infinită cu numere de la 1 la k și o poziție p aflată cu pe elemente mai sus decît primul element al spiralei să se spună ce valoare are elementul de pe acea poziție. Rezolvare problema medalion aici: [2]
• Am vorbit despre problema joc17, care are o implementare ușoară cu condiția să țineți toate matricele de căutat, inclusiv rotațiile lor, într-un vector de 12 matrice cu elemente zero și unu. Astfel, va trebui să declarați un tablou tridimensional inițializat. Necesită atenție la declararea acestui tablou, dar programul se simplifică, semănînd mult cu cel de căutare submatrice în matrice.
• Baze de numerație, conversie din baza zece în baza doi și invers
  • aplicație: să se afișeze toate submulțimile unei mulțimi
• Conversie din baza zece in baza 16 și invers.

Temă clasa a șasea

• problemele rămase din urmă, cu matrice: joc14, cifru, robinson
• din urmă: joc17 (oni 2011 clasa 7), cu rezolvarea simplă folosind tablouri tridimensionale
• dat un număr în baza 2 de maxim 30 de cifre să se afișeze conversia lui la baza 10
• dat un număr în baza 10 mai mic ca 2 miliarde să se afișeze conversia lui la baza 2
• probleme ONI 2011 clasa a 6-a: xy (joc16, talent altă dată)
• Opțional: tetris, bile6, trigrame la varena.ro (rezolvare trigrame aici [3])

Recursivitate, continuare

• Turnurile din hanoi. Mulți dintre voi ați rezolvat-o, felicitări! Problema este un exemplu frumos de recursivitate, deoarece rezolvarea ei este prin excelența recursivă. Iată o soluție "clasică" care include ideile din soluțiile voastre, dar e cît se poate de simplă: [4]

Despre structura de date coadă

• Ideea de tip de date abstract: un tip de date abstract este un model matematic, ca și automatele. Acest model definește operații asupra tipului de date, precum și restricții asupra efectului acestor operații.Tipurile de date abstracte sînt utile în simplificarea algoritmilor, deaorece descompun problema în subprobleme mai mici, cunoscute și studiate.
• Exemplu: tipul de date abstract coadă, care definește operațiile enqueue, care adaugă un element la coadă, și dequeue, care scoate un element din coadă. Restricțiile sînt asupra ordinii de returnare a elementelor și anume ele trebuie returnate după regula "primul venit primul plecat". De aceea se spune că o coadă este o structură de tip FIFO (first in, first out). Definim, de asemenea doua operații utile: empty (coadă goală) și full (coadă plină).

  

  Coada ca tip abstract de date

• Tipurile de date abstracte separă funcționalitatea de implementare. În cazul cozii există mai multe implementări posibile. Noi vom studia una dintre cele mai folosite.
• Implementarea cu vectori circulari
  • Folosește un vector pentru a păstra elementele și doi indici, primul și ultimul care memorează poziția primului, respectiv ultimului element din coadă. Pentru a nu deplasa elemente atunci cînd scoatem un element din coadă vom incrementa doar poziția primului element. Atunci cînd adăugăm un element în coadă incrementăm poziția ultimului element.
  • Pentru a refolosi golurile rămase în urmă la scoaterea din coadă și a nu deplasa cei doi indici la infinit vom defini o mărime maximă a cozii, n. Atunci cînd unul din indici depășește această mărime el revine la zero. Logic vorbind după ultimul element din vector urmează din nou primul. De aceea spunem că vectorul este circular. Formula de actualizare a indicilor devine primul = (primul + 1) % n și ultimul = (ultimul + 1) % n, unde n este numărul maxim de elemente din coadă.

    

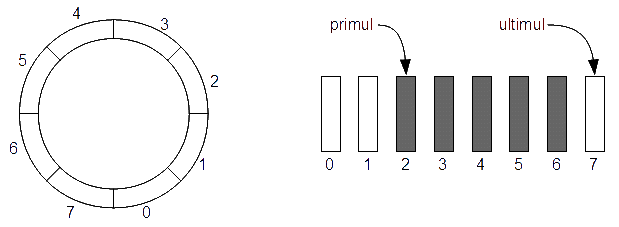
    Implementare coadă cu vector circular

  • Observăm că primul este poziția primului element din coadă, iar ultimul este poziția primului element liber din vector.
  • Coadă goală. Cum răspundem la întrebarea "este coada goală"? Se observă că acest lucru se întimplă cînd primul == ultimul.
  • Coada plină. Cum răspundem la întrebarea "este coada plină"? Observăm că aceasta se întîmplă tot atunci cînd primul == ultimul. Pentru a diferenția între aceste două cazuri vom "sacrifica" un element din vector, folosind numai n-1 poziții. În felul acesta testul de coadă plină va fi (ultimul + 1) % n = primul.
• În această implementare cele patru operații au complexitate O(1).
• Unul din avantajele acestei implementări, de care veți auzi în detaliu în facultate este că scoaterea de elemente se poate face în paralel cu adăugarea, de exemplu în cazul cînd un proces generează elementele de adăugat și un alt proces, independent, colectează elementele spre procesare.

Maximum în fereastră glisantă (maximum over a sliding window)

• Enunț: dîndu-se un șir de n numere considerăm cele n – k + 1 subsecvențe de k numere consecutive în șir (denumite și "ferestre" de lungime k). Putem vedea aceste ferestre ca pe o singura fereastră, deplasabilă, care ne dă acces la k elemente din vector odată. Se cere ca pentru fiecare fereastră să se găsească maximul.
• Algoritmul de rezolvare trivial (forță brută) recalculează maximul pentru fiecare din ferestre, avînd complexitate O(kn).
• Pentru a reduce complexitatea găsirii maximului procedăm astfel: luăm prima fereastră, de la 0 la k-1. Să spunem că maximul se află pe poziția p1. Pe măsură ce vom deplasa fereastra este imposibil ca elementele din-naintea maximului să fie vreodată maximul ferestrei, deoarece ele vor face parte împreună cu maximul din această fereastră. Să considerăm poziția celui mai mare element după maxim și la dreapta lui, în fereastră. Fie ea p2. Rezultă că nici un element pe pozițiile intermediare i, p1 < i < p2, nu poate fi vreodată maxim în fereastră, deoarece aceste elemente vor fi împreună cu p2 în toate ferestrele care le conțin. Similar, considerînd p3 poziția următorului maxim, nici un element între p2 și p3 nu va putea fi maxim. Astfel apare următorul algoritm: memorăm toate maximele descrescătoare din prima fereastră, într-o coadă. Primul element din coadă este maximul ferestrei. Cînd deplasăm fereastra trebuie să actualizăm structura de maxime din coadă. Pentru aceasta dăm atenție elementului care dispare din fereastră și celui care intră în fereastră. Dacă elementul care iese nu este maximul curent, nu avem nimic de făcut. Dacă este maximul curent vom scoate primul element din coada de maxime. Dacă elementul proaspăt adăugat în fereastră este mai mic decît ultimul maxim din coadă se adaugă la coadă. În caz contrar el va "arunca" ultimul element, iar apoi încercăm din nou. Rezultă că noul element din fereastră "aruncă" toate elementele de la urma cozii strict mai mic ca el, iar apoi îl adăugăm normal la coadă.

  

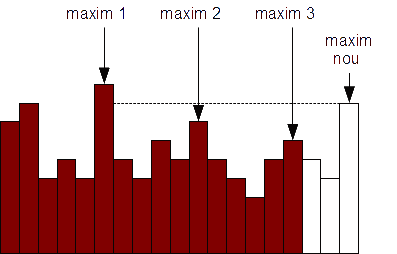
  În figură noul maxim va elimina din coadă maximele 2 și 3. Coada rămasă va conține maximul 1 și maximul nou

• La prima vedere pare că acest algoritm are complexitate O(kn). Folosind analiza amortizată putem calcula complexitatea reală ca fiind O(n).
• Memoria suplimentară folosită este mărimea maximă a cozii, adică O(k).
• Observăm că putem folosi acest algoritm la problema cuburi4. Genul acesta de prelucrare, eliminarea unor cifre ale unui număr astfel încît numărul rămas să fie maxim (sau minim) apare des la olimpiade.

Temă clasa a șaptea și a opta

• Problema maxim la vianuarena în O(n) timp și O(1) memorie folosind algoritmul anterior de maximum în fereastră glisantă. Atenție, algoritmul clasic folosește O(k) memorie, nu O(1)!
• Problema trigrame la varena.ro (rezolvare trigrame aici [5])
• Opțional: Turnurile din Hanoi iterativ. Programul este aproape la fel de scurt, odată ce ați găsit algoritmul ☺. Rezolvare aici [6]
• Opțional: puncte5.
• Opțional: zeratul