Clasa a V-a lecția 12 - 26 oct 2017
Tema – rezolvări
Rezolvări aici [1]
Lecție
<html5media height="720" width="1280">https://www.algopedia.ro/video/2017-2018/2017-10-26-lectie-info-12-720p.mp4</html5media>
Exerciții
Scrieți schema logică și programul C pentru următoarele probleme, folosind fișiere pentru citirea și scrierea datelor.
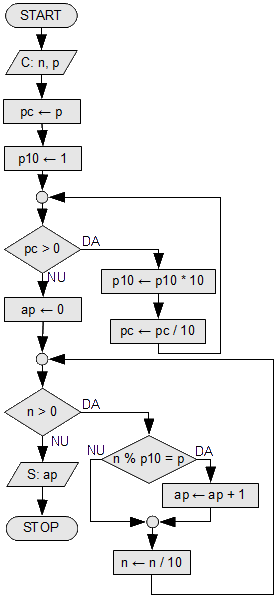
Număr conținut în alt număr
Să se spună de cîte ori un număr conține pe altul. Exemplu: 439453967 conține 39 de două ori, iar 2323232 conține 232 de 3 ori. Iată o variantă de algoritm. Acest algoritm nu funcționează într-un caz particular. Puteți spune cînd? Cum putem repara problema?
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, p, pc, p10, ap;
fin = fopen( "aparitii.in", "r" );
fscanf( fin, "%d%d", &n, &p );
fclose( fin );
// calculam numarul de cifre al lui p
pc = p;
p10 = 1;
while ( pc > 0 ) {
p10 = p10 * 10;
pc = pc /10;
}
// comparam cu ultimele cifre ale lui n
ap = 0;
while ( n > 0 ) {
if ( n % p10 == p )
ap = ap + 1;
n = n / 10;
}
fout = fopen( "aparitii.out", "w" );
fprintf( fout, "%d\n", ap );
fclose( fout );
return 0;
} |
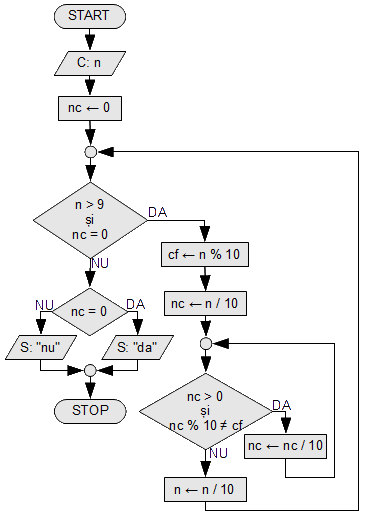
Număr cu cifre distincte
Să se spună dacă un număr are toate cifrele distincte. Exemplu: 439453967 nu are cifre distincte, cifrele 3 și 9 apar de două ori în număr; Numărul 4539 are cifre distincte, nici o cifră a sa nu se repetă.
Rezolvarea 1
O soluție posibilă este să luăm ultima cifră a numărului n, să o eliminăm din număr, iar apoi să verificăm că numărul rămas nu conține cifra. Dacă totul este în regulă reluăm procedeul cu numărul rămas. Repetăm pînă ce n rămîne de o singură cifră (care nu se poate repeta).
Iată o variantă posibilă pentru această soluție:
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, nc, cf;
fin = fopen( "distincte.in", "r" );
fscanf( fin, "%d", &n );
fclose( fin );
nc = 0;
while ( n > 9 && nc == 0 ) {
cf = n % 10;
nc = n / 10;
while ( nc > 0 && nc % 10 != cf )
nc = nc / 10;
n = n / 10;
}
fout = fopen( "distincte.out", "w" );
if ( nc == 0 )
fprintf( fout, "Cifre distincte\n" );
else
fprintf( fout, "Cifre nedistincte\n" );
fclose( fout );
return 0;
} |
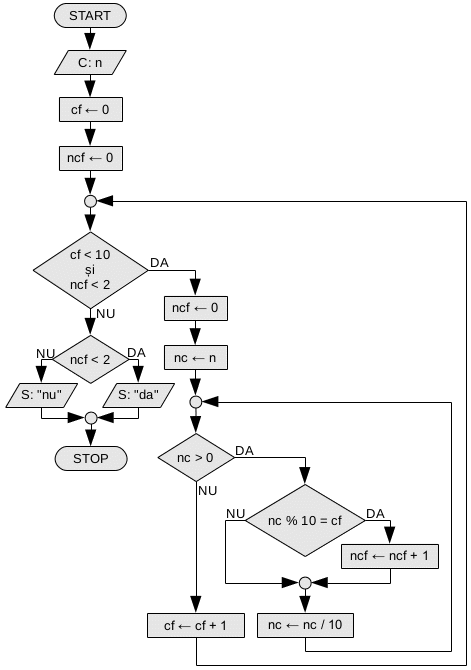
Rezolvarea 2
O altă soluție ar putea fi să luăm toate cifrele de la 0 la 9 și să numărăm de cîte ori apar în numărul n. Ne oprim dacă găsim că o cifră apare de două sau mai multe ori (este OK să apară de zero ori sau o singură dată).
Iată o variantă posibilă pentru această soluție:
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, cf, nc, ncf;
fin = fopen( "distincte.in", "r" );
fscanf( fin, "%d", &n );
fclose( fin );
cf = 0;
ncf = 0;
while ( cf < 10 && ncf < 2 ) {
ncf = 0;
nc = n;
while ( nc > 0 ) {
if ( nc % 10 == cf )
ncf = ncf + 1;
nc = nc / 10;
}
n = n / 10;
cf = cf + 1;
}
fout = fopen( "distincte.out", "w" );
if ( ncf < 2 )
fprintf( fout, "Cifre distincte\n" );
else
fprintf( fout, "Cifre nedistincte\n" );
fclose( fout );
return 0;
} |
Care variantă este mai bună? Să analizăm. Prima variantă testează strict cifrele distincte ale numărului, oprindu-se cînd găsește o cifră care se repetă. Astfel, ea va testa maxim toate cele zece cifre. A doua variantă va testa din start toate cele zece cifre, cu excepția cazului cînd găsește o cifră care apare de două sau mai multe ori. Drept care a doua variantă va testa întotdeauna mai multe cifre decît prima variantă. Prima variantă este deci mai bună.
Secvențe
Definiție: denumim secvență un șir de numere. Exemplu: 34 20 4 0 12 5 8 7. Simplu?
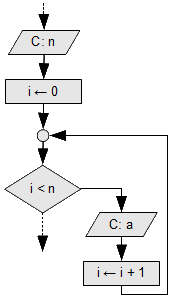
Citirea unei secvențe
Deoarece nu avem unde păstra numerele unei secvențe, le vom citi, pe rînd, în aceeași variabilă. Pentru a ști cîte numere citim (cîte numere are secvența) de obicei vom citi mai întîi numărul de numere din secvență, n și apoi cele n numerele din secvență, într-o buclă WHILE-DO. Exemplu:
 |
fscanf( fin, "%d", &n );
i = 0;
while ( i < n ) {
fscanf( fin, "%d", &a );
i = i + 1;
} |
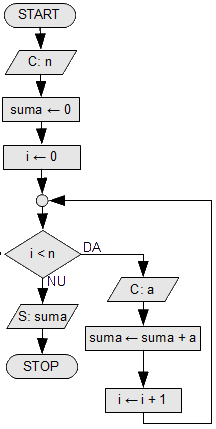
Suma unei secvențe
Ca prim exemplu de lucru cu secvențe să calculăm suma a n numere citite la intrare:
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, i, a, suma;
fin = fopen( "suma.in", "r" );
fscanf( fin, "%d", &n );
suma = 0;
i = 0;
while ( i < n ) {
fscanf( fin, "%d", &a );
suma = suma + a;
i = i + 1;
}
fclose( fin );
fout = fopen( "suma.out", "w" );
fprintf( fout, "%d", suma );
fclose( fout );
return 0;
} |
Exemple:
| Fișierul suma.in | Fișierul suma.out |
|---|---|
| 3 4 2 6 |
12 |
| 5 25 10 8 0 4 |
47 |
Observații:
- variabila i se numește contor, deoarece ea contorizează numărul de execuții al buclei WHILE-DO. Pentru a executa o buclă de n ori inițializăm contorul cu 0 și ne oprim cînd devine egal cu n. Preferăm această variantă, față de a porni cu i de la 1, deoarece ne obișnuiește pentru viitor să lucrăm corect cu vectori.
- Variabila suma se numește acumulator, deoarece în ea se acumulează rezultatul, pe măsură ce citim secvența. Orice variabilă de tip acumulator trebuie inițializată înainte de a începe calculele! În acest caz, deoarece este o sumă, ea se va inițializa cu 0, deoarece 0 este elementul neutru la adunare. Dacă am fi calculat produsul secvenței am fi inițializat acumulatorul cu 1, deoarece 1 este elementul neutru la înmulțire.
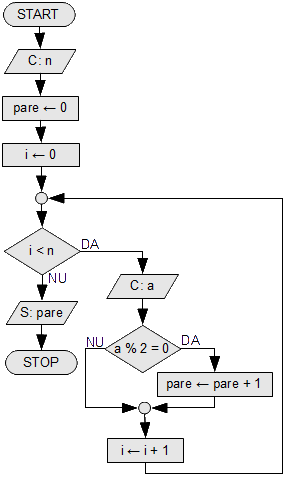
Numărul de elemente pare din secvență
Să se afișeze cîte elemente pare se află într-o secvență
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, i, a, pare;
fin = fopen( "pare.in", "r" );
fscanf( fin, "%d", &n );
pare = 0;
i = 0;
while ( i < n ) {
fscanf( fin, "%d", &a );
if ( a % 2 == 0 )
pare = pare + 1;
i = i + 1;
}
fclose( fin );
fout = fopen( "pare.out", "w" );
fprintf( fout, "%d", pare );
fclose( fout );
return 0;
} |
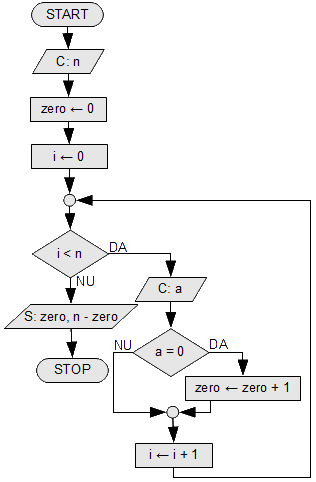
Numărul de elemente zero și diferite de zero din secvență
Să se calculeze cîte numere zero apar într-o secvență, precum și cîte numere diferite de zero.
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, i, a, zero;
fin = fopen( "zero.in", "r" );
fscanf( fin, "%d", &n );
zero = 0;
i = 0;
while ( i < n ) {
fscanf( fin, "%d", &a );
if ( a == 0 )
zero = zero + 1;
i = i + 1;
}
fclose( fin );
fout = fopen( "zero.out", "w" );
fprintf( fout, "%d %d", zero, n - zero );
fclose( fout );
return 0;
} |
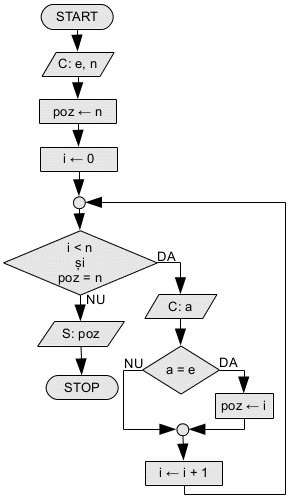
Căutare număr în secvență
Să se spună dacă un număr e apare într-o secvență și pe ce poziție. Dacă e apare în secvență se va afișa poziția primei apariții a lui, între 0 și n - 1. În caz contrar se va afișa n.
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, i, a, e, poz;
fin = fopen( "caut.in", "r" );
fscanf( fin, "%d%d", &e, &n );
poz = n;
i = 0;
while ( i < n && poz == n ) {
fscanf( fin, "%d", &a );
if ( a == e )
poz = i;
i = i + 1;
}
fclose( fin );
fout = fopen( "caut.out", "w" );
fprintf( fout, "%d", poz );
fclose( fout );
return 0;
} |
Observații:
- Variabila poz are dublu rol. Pe de o parte ea memorează poziția primei apariții a numărului e în secvență. Pe de altă parte ea ne spune dacă am găsit numărul, astfel încît să ieșim din bucla WHILE-DO imediat ce am găsit numărul e. Variabilele care semnalează îndeplinirea unei condiții de oprire se numesc stegulețe, deci putem spune că variabila poz este un steguleț.
Tema
- Tema 12: să se rezolve următoarele probleme (schemă logică + program C în CodeBlocks, trimis la vianuarena):
- Problemă de logică: dispunem de 3000 de banane pe care vrem să le transportăm din orașul A în orașul B aflate la 1000km distanță. Dispunem de o cămilă care poate să care maxim 1000 de banane. În timp ce mergea ea mănîncă o banană la fiecare kilometru. Care este numărul maxim de banane pe care le puteți duce din A în B și cum procedați? Puteți desigur să depozitați banane în orice loc de pe drum.
Rezolvări aici [2]
