Psihologia concursurilor de informatică/6 Probleme de concurs 2: Difference between revisions
No edit summary |
(No difference)
|
Latest revision as of 14:38, 9 March 2018
⇦ înapoi la Psihologia concursurilor de informatică
Capitolul VI: Probleme de concurs (7-12)
Problema 7
Problema programării unui turneu de fotbal a fost dată spre rezolvare la a III-a Balcaniadă de Informatică, Varna 1995. Vom prezenta mai întâi enunțul nemodificat al problemei, după care vom adăuga câteva detalii care o vor face mai „provocatoare”.
ENUNȚ: Una din sarcinile Ministerului Sporturilor dintr-o țară balcanică este de a organiza un campionat de fotbal cu N echipe (numerotate de la 1 la N). Campionatul constă din N etape (dacă N este impar) sau N-1 etape (dacă N este par); orice două echipe dispută între ele un joc și numai unul. Scrieți un program care realizează o programare a campionatului.
Intrarea: Numărul de echipe N (2 ≤ N ≤ 24) va fi dat la intrarea standard (tastatură).
Ieșirea se va face în fișierul text OUTPUT.TXT sub forma unui tabel cu numere întregi avînd N linii. Al j-lea element din linia i este numărul echipei care joacă cu echipa i în etapa j (evident, dacă i joacă cu k în etapa j, atunci în tabel k joacă cu i în aceeași etapă). Dacă echipa i este liberă în etapa j, atunci al j-lea element al liniei i este zero.
Exemple:
| INPUT.TXT | OUTPUT.TXT |
|---|---|
| 3 | 2 3 0 1 0 3 |
| 4 | 2 3 4 1 4 3 |
Timp de implementare: circa 1h 45’
Timp de execuție: 33 secunde
Iată și modificările pe care le propunem pentru a aduce cu adevărat problema la nivel de concurs:
- Limita pentru numărul de echipe este N ≤ 200;
- Timpul de implementare este de 45 minute;
- Timpul de execuție este de 2-3 secunde;
- Complexitatea cerută este .
REZOLVARE: Vom lăsa pe seama cititorului conceperea, implementarea și testarea unei rezolvări backtracking (adoptată de majoritatea în timpul concursului). De altfel, la Balcaniadă concurenții au avut la dispoziție calculatoare 486 / 50 Mhz, iar un backtracking îngrijit funcționa cam până la N = 18 în timpul impus, ceea ce asigura cam 75% din punctajul maxim. În afară de aceasta, se mai puteau face și alte lucruri nu tocmai elegante, având în vedere că datele de ieșire nu erau foarte mari. Pentru N>18, mulți concurenți lăsau programul să meargă până când termina (câteva minute bune sau chiar mai mult), apoi scriau rezultatele într-un fișier temporar. Matricea rezultată era inclusă ca o constantă în codul sursă. Programul care era dat comisiei de corectare se prefăcea că „se gândește” timp de câteva secunde, apoi scria pur și simplu matricea în fișierul de ieșire. Cu aceasta s-au luat punctaje foarte apropiate de maxim. Totuși, pentru N=24 un backtracking ar fi stat foarte mult pentru a găsi soluția. Tot timpul acesta, calculatorul era blocat, neputând fi folosit. De aceea, mulți concurenți nu au luat punctajul maxim, preferând să renunțe la ultimele teste și să rezolve celelalte probleme. Oricum, backtracking-ul este în acest caz o soluție pentru care raportul punctaj obținut / timp consumat este foarte convenabil.
Există însă și o soluție care poate asigura un punctaj maxim fără bătăi de cap și fără să folosească „date preprocesate”. Ea are complexitatea și nu face decât o singură parcurgere a matricei de ieșire. Ce-i drept, autorul a pierdut cam trei ore pentru a o găsi și implementa în timp de concurs, compromițând aproape rezolvarea celorlalte două probleme din ziua respectivă, dar comisia de corectare a fost plăcut impresionată, programul fiind singurul care mergea instantaneu. Rămâne ca voi să alegeți între eleganță și eficiență...
Dacă ținem cont și de restricțiile suplimentare propuse, rezolvarea backtracking nu mai este valabilă. În această situație, iată care este metoda care stă la baza rezolvării în timp pătratic. În primul rând se reduce cazul când N este impar la un caz când N este par, prin mărirea cu 1 a lui N și introducerea unei echipe fictive. În fiecare etapă se consideră că echipa care trebuia să joace cu echipa fictivă stă de fapt „pe bară”. Iată de exemplu cum se rezolvă cazul N=3:
a) Se programează un campionat cu 4 echipe, echipa 4 fiind echipa fictivă:
| Echipa | Etapa 1 | Etapa 2 | Etapa 3 |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| 2 | 1 | 4 | 3 |
| 3 | 4 | 1 | 2 |
| 4 | 3 | 2 | 1 |
b) Se neglijează ultima linie din tabel, meciurile echipei fictive nefiind importante:
| Echipa | Etapa 1 | Etapa 2 | Etapa 3 |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| 2 | 1 | 4 | 3 |
| 3 | 4 | 1 | 2 |
c) Peste tot unde apare cifra 4, ea este înlocuită cu 0:
| Echipa | Etapa 1 | Etapa 2 | Etapa 3 |
|---|---|---|---|
| 1 | 2 | 3 | 0 |
| 2 | 1 | 0 | 3 |
| 3 | 0 | 1 | 2 |
Mai rămâne să vedem cum se tratează cazul când N este par. E destul de greu de dat o demonstrație matematică metodei care urmează; de fapt, nici nu există una, problema fiind rezolvată în timp de concurs prin inducție incompletă (adică s-a constatat cu creionul pe hârtie că metoda merge pentru N=4, 6, 8 și 10, apoi s-a scris programul care să facă același lucru și s-a constatat că merge și pentru valori mai mari). Să tratăm și aici cazul N=8, apoi să generalizăm procedeul.
Vor fi șapte etape și, fără a reduce cu nimic generalitatea problemei, putem presupune că echipa 1 joacă pe rând cu echipele 2, 3, 4, 5, 6, 7 și 8. Deocamdată tabelul arată astfel:
| Echipa | Etapa 1 | Etapa 2 | Etapa 3 | Etapa 4 | Etapa 5 | Etapa 6 | Etapa 7 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 1 | ||||||
| 3 | 1 | ||||||
| 4 | 1 | ||||||
| 5 | 1 | ||||||
| 6 | 1 | ||||||
| 7 | 1 | ||||||
| 8 | 1 |
Echipa 2 are deja programat un meci cu echipa 1 în prima etapă și mai are de programat meciurile cu echipele 3, 4, 5, 6, 7 și 8 în celelalte etape. Așezarea se poate face oricum, cu condiția ca echipele 1 și 2 să nu își aleagă același partener în aceeași etapă. De exemplu, putem programa meciul 2-3 în etapa a 3-a, meciul 2-4 în etapa a 4-a, ..., iar meciul 2-8 în etapa a 2-a. Astfel am completat linia a doua a tabloului:
| Echipa | Etapa 1 | Etapa 2 | Etapa 3 | Etapa 4 | Etapa 5 | Etapa 6 | Etapa 7 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 1 | 8 | 3 | 4 | 5 | 6 | 7 |
| 3 | 1 | 2 | |||||
| 4 | 1 | 2 | |||||
| 5 | 1 | 2 | |||||
| 6 | 1 | 2 | |||||
| 7 | 1 | 2 | |||||
| 8 | 2 | 1 |
Echipa 3 are programate meciurile cu 1 și 2 și mai are de programat meciurile cu echipele 4, 5, 6, 7 și 8. Pentru a nu crea conflicte (adică două echipe să nu-și aleagă același adversar), putem aplica același procedeu: pornim de la etapa a 5-a și completăm toate celulele goale ale liniei a 3-a cu numerele de la 4 la 8, mergând circular spre dreapta:
| Echipa | Etapa 1 | Etapa 2 | Etapa 3 | Etapa 4 | Etapa 5 | Etapa 6 | Etapa 7 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 1 | 8 | 3 | 4 | 5 | 6 | 7 |
| 3 | 7 | 1 | 2 | 8 | 4 | 5 | 6 |
| 4 | 1 | 2 | 3 | ||||
| 5 | 1 | 2 | 3 | ||||
| 6 | 1 | 2 | 3 | ||||
| 7 | 3 | 1 | 2 | ||||
| 8 | 2 | 3 | 1 |
Se folosește aceeași metodă pentru a completa și celelalte linii ale matricei. Pentru fiecare linie i (i ≤ N-1):
- Se caută pe linia i apariția valorii i-1;
- Se caută primul spațiu liber (mergând circular spre dreapta). Primul spațiu liber înseamnă prima etapă în care se poate programa meciul dintre echipele i și i+1 (trebuie ca ambele să fie libere în acea etapă). Se constată experimental că trebuie început de la a doua poziție liberă de după apariția valorii i-1;
- Se merge circular spre dreapta și, în căsuțele libere întâlnite se trec valorile i+1, i+2, ..., N. Concomitent, pe aceleași coloane ale liniilor i+1, i+2, ..., N se trece valoarea i.
| Echipa | Etapa 1 | Etapa 2 | Etapa 3 | Etapa 4 | Etapa 5 | Etapa 6 | Etapa 7 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 1 | 8 | 3 | 4 | 5 | 6 | 7 |
| 3 | 7 | 1 | 2 | 8 | 4 | 5 | 6 |
| 4 | 6 | 7 | 1 | 2 | 3 | 8 | 5 |
| 5 | 8 | 6 | 7 | 1 | 2 | 3 | 4 |
| 6 | 4 | 5 | 8 | 7 | 1 | 2 | 3 |
| 7 | 3 | 4 | 5 | 6 | 8 | 1 | 2 |
| 8 | 5 | 2 | 6 | 3 | 7 | 4 | 1 |
Fiecare linie a matricei poate fi parcursă in acest fel de maxim 2 ori (o dată pentru găsirea coloanei de start și o dată pentru completarea liniei), deci numărul total de celule vizitate este cel mult . Complexitatea pătratică este cea optimă, deoarece programul trebuie în orice caz să tipărească la ieșire circa numere.
#include <stdio.h>
#define NMax 200
unsigned char A[NMax+1][NMax+1];
int N,RealN;
void FindNextFree(int Line,int *K)
/* Cauta (circular) urmatorul spatiu liber pe linia Line */
{ do *K=*K%(N-1)+1;
while (A[Line][*K]);
}
void MakeMatrix(void)
{ int i,j,k;
for (i=1;i<=N;i++)
for (j=1;j<=N;j++) A[i][j]=0;
for (i=1;i<N;i++) /* Pentru fiecare echipa */
{ if (i==1) /* Alege coloana de start */
j=1;
else { j=0;
do j++; while (A[i][j]!=i-1);
FindNextFree(i,&j);
FindNextFree(i,&j);
}
for (k=i+1;k<=N;k++) /* Completeaza circular linia */
{ A[i][j]=k;
A[k][j]=i;
if (k<N) FindNextFree(i,&j);
}
}
}
void WriteMatrix(void)
{ int i,j;
FILE *F=fopen("output.txt","wt");
for (i=1;i<=RealN;i++)
{ for (j=1;j<N;j++)
fprintf(F,"%4d",A[i][j]>RealN ? 0 : A[i][j]);
fprintf(F,"\n");
}
fclose(F);
}
void main(void)
{
printf("N=");scanf("%d",&RealN);
N=RealN+RealN%2; /* Se adauga 1 daca RealN e impar */
MakeMatrix();
WriteMatrix();
}
Problema 8
Problema codului lui Pruffer[1] pentru arborii generali, mai exact cea a decodificării acestui cod, este genul de problemă care nu este excesiv de grea, dar care necesită un artificiu fără de care nu se poate ajunge la complexitatea optimă.
ENUNȚ: Un arbore general neorientat conex cu N+2 vârfuri se poate codifica eficient printr-un vector cu N numere, astfel:
- Numerotăm nodurile de la 1 la N+2 într-o ordine oarecare;
- Eliminăm cea mai mică frunză (nod de grad 1) și adăugăm în vector numărul nodului de care ea aparținea;
- Reluăm procedeul pentru arborele rămas: tăiem cea mai mică frunză și adăugăm în vector numărul nodului de care ea aparținea;
- Repetăm procedeul până mai rămân doar două noduri.
Vectorul rezultat se numește codificare Pruffer a arborelui dat. Iată un exemplu de construcție a codului Pruffer atașat arborelui din figura de mai jos:
Codul lui Pruffer se obține astfel:
- Îl tăiem pe 3 și scriem 1;
- Îl tăiem pe 4 și scriem 5;
- Îl tăiem pe 6 și scriem 2;
- Îl tăiem pe 2 și scriem 5;
- Îl tăiem pe 5 și scriem 1;
Deci codificarea este (1, 5, 2, 5, 1) (și mai rămâne muchia 1-7, lucru care este evident, deoarece 1 și 7 sunt singurele noduri care nu au fost tăiate).
Așadar fiecărui arbore oarecare cu N+2 noduri i se poate atașa un vector cu N componente numere naturale cuprinse între 1 și N+2. Se poate demonstra că funcția definită între cele două mulțimi (mulțimea arborilor și mulțimea vectorilor) este bijectivă. De aici rezultă două lucruri:
- Există arbori generali cu N+2 noduri.
- Codificarea Pruffer admite și decodificare (deoarece funcția de codificare este bijectivă). Tocmai aceasta este problema de rezolvat. Se dă un vector de N numere întregi, fiecare cuprins între 1 și N+2. Se cere să se tipărească cele N+1 muchii ale arborelui decodificat.
Intrarea se face din fișierul text INPUT.TXT care conține două linii. Pe prima linie se dă N (1 ≤ N ≤ 10000), pe a doua cele N numere separate prin spații.
Ieșirea se va face în fișierul text OUTPUT.TXT. Acesta va conține muchiile arborelui, câte una pe linie, o muchie fiind indicată prin vârfurile adiacente separate printr-un spațiu.
Exemplu:
| INPUT.TXT | OUTPUT.TXT |
|---|---|
| 5 1 5 2 5 1 |
5 2 1 3 |
Timp de implementare: 45 minute.
Timp de rulare: 2-3 secunde.
Complexitate cerută: .
REZOLVARE: Să pornim de la exemplul particular prezentat mai sus, urmând ca apoi să generalizăm algoritmul.
Primim la intrare N=5 (deducem că arborele are 7 noduri) și codificarea (1, 5, 2, 5, 1). Primul element din vector este 1. Știm deci că, la primul pas, a fost eliminată o frunză al cărei părinte este nodul 1. Întrebarea este: ce număr purta respectiva frunză? În nici un caz 1, deoarece numărul 1 îl avea tatăl ei. Nici 2, nici 5 nu ar putea fi, deoarece aceste numere apar mai târziu în codificare, deci „mai este nevoie” de ele și nu pot fi încă eliminate. Rămân 3, 4, 6 și 7. Dintre acestea noi știm că a fost tăiată cea mai mică frunză. Este însă ușor de văzut că toate nodurile enumerate sunt frunze în arborele inițial (deoarece nu mai apar în vector, adică nici un alt nod nu mai este legat de ele), deci îl vom alege pe cel mai mic cu putință, adică pe 3. Rezultă că prima muchie tăiată a fost (1,3).
Pe poziția a doua în codificare apare numărul 5. Ce număr ar putea avea frunza tăiată? 1 și 2 mai apar ulterior în codificare deci nu pot fi eliminate încă, 5 este chiar tatăl frunzei necunoscute, iar 3 a fost deja eliminat. Dintre 4, 6 și 7, frunza cu numărul cel mai mic este 4, deci următoarea muchie tăiată este (4,5).
În continuare apare un 2. Cel mai mic nod care nu mai apare în vector și nici nu a fost deja eliminat este 6, deci muchia este (6,2). Se observă că mai departe nu mai apare nici un 2 în codificare, de unde deducem că după tăierea nodului 6, nodul 2 a devenit frunză și va putea fi la rândul său eliminat. Cu un raționament analog, următoarele muchii eliminate sunt (2,5) și (5,1), iar singurele noduri rămase sunt 1 și 7. Arborele a fost reconstituit corect.
Deci procedeul general este: pentru fiecare număr dintre cele N din vector, nodul care aparținea de el poartă cel mai mic număr care nu intervine ulterior în codificare și nu a fost tăiat deja. Astfel se generează N muchii. A N+1-a muchie are drept capete ultimele noduri rămase netăiate.
Acesta este algoritmul. Trebuie să ne ocupăm acum de partea de implementare.
Pentru a testa la orice moment dacă un nod mai apare sau nu în vector, este bine să se creeze la citirea datelor un vector care să rețină numărul de apariții în codificare al fiecărui nod. Pentru exemplul dat, vectorul de apariții va fi Apar=(2,1,0,0,2,0,0), semnificând că 1 și 5 apar de câte două ori, 2 apare o singură dată, iar 3, 4, 6 și 7 nu apar deloc. La fiecare pas, când se „restaurează” o muchie, se decrementează poziția corespunzătoare tatălui în vectorul de apariții. Un număr nu mai apare ulterior în codificare dacă pe poziția sa din vectorul de apariții se află un 0.
Astfel, o primă versiune de program ar putea fi:
intrare: N, V[1..N]. construieste vectorul Apar[1..N+2] pentru i de la 1 la N: cauta primul j pentru care Apar[j]=0 si j nu a fost taiat; scrie muchia (j,V[i]); Apar[j] = Apar[j]-1; marcheaza nodul j ca fiind taiat.
După cum se observă, căutarea celui mai mic nod j se face în timp liniar, ceea ce înseamnă că algoritmul complet va necesita un timp pătratic. Pentru a-l reduce la o complexitate liniară, începem prin a observa că la fiecare pas alegem frunza cu numărul cel mai mic. Aceasta înseamnă că, în general, numărul frunzei alese spre a fi tăiată va crește la fiecare pas. Astfel, prima oară am tăiat nodul 4, apoi nodul 7. Singurul caz când va fi tăiată o frunză mai mică decât cea dinaintea ei este atunci când unui nod cu număr mic i se taie toate frunzele și devine el însuși o frunză, putănd fi tăiat. În exemplul nostru, nodul 2 nu putea fi eliminat de la început, deși avea un număr mic, deoarece mai avea atașată frunza 6. După eliminarea muchiei (6,2), nodul 2 a devenit frunză și a fost eliminat imediat.
Putem deci păstra într-o variabilă (care în program se numește Next) următoarea frunză care care trebuie eliminată. Dacă prin decrementarea numărului de apariții la pasul curent nu s-a creat nici un zero în vectorul Apar, sau s-a creat un zero, dar pe o poziție K>Next, atunci totul este bine și la pasul următor se va elimina nodul Next. Dacă s-a creat un zero pe o poziție K mai mică decât Next, rezultă că în arbore există acum două frunze, K și Next, K fiind mai mică, deci prioritară. Atunci la pasul următor se va elimina frunza de pe poziția K, urmând ca peste doi pași să se revină la frunza Next. Dacă prin eliminarea acestei frunze K s-a creat un alt zero în vectorul de apariții, tot pe o poziție K’ mai mică decât Next, se va trece mai întâi la acea poziție, urmând ca după aceea să se revină la poziția Next etc.
La prima vedere, pare necesară menținerea unei stive în care să depunem numerele Next, K, K’... și să le scoatem din stivă pe măsură ce nodurile respective sunt eliminate. Acest lucru ar presupune în continuare un algoritm pătratic. Totuși nu este așa deoarece, odată ce am tăiat un nod și l-am marcat ca atare, putem fi siguri că nu ne vom mai intâlni cu el până la sfârșitul decodificării, deci nu mai este necesară stocarea lui. Există o pseudo-stivă care are înălțimea 2: frunza asupra căreia se operează curent și nodul care urmează, Next.
În acest fel, numărul total de incrementări al variabilei Next nu depășește N (iar ea nu este niciodată decrementată), deci programul este rezolvat în timp liniar. Facem observația că algoritmul este optim; nu poate exista unul mai bun deoarece există muchii care trebuie tipărite.
#include <stdio.h>
#define NMax 10002
typedef int Vector[NMax];
Vector V,Apar;
int N;
void ReadData(void)
{ int i;
FILE *InF=fopen("input.txt","rt");
fscanf(InF,"%d",&N);
for (i=1;i<=N+2;Apar[i++]=0);
for (i=1;i<=N;i++)
{ fscanf(InF,"%d",&V[i]);
Apar[V[i]]++;
}
fclose(InF);
}
void Decode(void)
{ int Current=0,Next,i;
FILE *OutF=fopen("output.txt","wt");
do; while (Apar[++Current]); /* Se cauta prima frunza */
Next=Current;
for (i=1;i<=N;i++)
{ fprintf(OutF,"%d %d\n",Current,V[i]);
if (Current==Next) do; while (Apar[++Next]);
/* Daca am ajuns la ultimul 0, mai caut unul */
Apar[V[i]]--;
Current=(V[i]<Next) && (Apar[V[i]]==0) ? V[i] : Next;
/* Daca exista o frunza mai mica decat Next, */
/* ea este prioritara, altfel revin la Next */
}
fprintf(OutF,"%d %d\n",Current,Next);
fclose(OutF);
}
void main(void)
{
ReadData();
Decode();
}
Problema 9
Iată o problemă care necesită pentru reducerea complexității un artificiu asemănător celui din problema codului Pruffer. Ea a fost propusă în 1995 la concursul de selecție a echipelor României pentru IOI și CEOI. Deși cerința este puțin modificată pentru a nu ne izbi de dificultăți secundare, ideea generală de abordare este aceeași.
ENUNȚ: Președintele companiei X dorește să organizeze o petrecere cu angajații. Această companie are o structură ierarhică în formă de arbore. Fiecare angajat are asociat un număr întreg reprezentând măsura sociabilității sale. Pentru ca petrecerea să fie agreabilă pentru toți participanții, președintele dorește să facă invitațiile astfel încât:
- el însuși să participe la petrecere;
- pentru nici un participant la petrecere să nu fie invitat și șeful lui direct;
- suma măsurilor sociabilităților invitaților să fie maximă.
Se cere să se spună care este suma maximă a sociabilităților care se poate obține.
Intrarea se face din fișierul INPUT.TXT care conține trei linii de forma:
N T(1) T(2) ... T(N) S(1) S(2) ... S(N)
unde N este numărul de angajați ai companiei, inclusiv președintele (N ≤ 1000), T(k) este numărul de ordine al șefului direct al lui k (dacă T(k) = 0, atunci k este președintele), iar S(k) este măsura sociabilității lui k. Valorile vectorului S sunt de tipul întreg.
Ieșirea: Pe ecran se va tipări suma maximă a sociabilităților ce se poate obține.
Exemplu: Pentru intrarea:
7 2 5 2 5 0 4 2 2 5 3 13 8 4 3
pe ecran se va afișa numărul 20 (fiindcă la petrecere participă 1, 3, 5, 6 și 7).
Timp de implementare: 1h - 1h 15’.
Timp de rulare: 2-3 secunde.
Complexitate cerută: . De asemenea, menționăm că s-a specificat N ≤ 1000 numai pentru ca programul sursă de mai jos să nu se complice și să distragă atenția asupra unor lucruri neimportante. În mod normal, limita trebuia să fie N ≤ 10000.
REZOLVARE: Vom expune mai întâi principiul de rezolvare al problemei, apoi vom aborda detaliile de implementare.
Algoritmul are la bază programarea dinamică și necesită o parcurgere de jos în sus a arborelui, decizia pentru fiecare nod depinzând de valorile tuturor fiilor lui. Ne propunem să aflăm două caracteristici pentru fiecare nod k:
- P(k) - suma maximă a sociabilităților care se poate obține în subarborele de rădăcină k în cazul în care k participă la petrecere;
- Q(k) - suma maximă a sociabilităților care se poate obține în subarborele de rădăcină k în cazul în care k nu participă la petrecere;
Dacă reușim să determinăm aceste caracteristici, nu ne rămâne decât să-l tipărim pe P(R) (R fiind rădăcina arborelui). Într-adevăr, problema cere să se determine suma maximă a sociabilităților din întregul arbore, adică din subarborele de rădăcină R. În plus, se mai cere ca R să participe la petrecere. Rămâne de aflat cum se stabilește relația între caracteristicile unui nod și cele ale fiilor săi.
- Dacă angajatul k participă la petrecere, atunci automat nici unul din subordonații săi direcți nu participă, și obținem relația:
- , j fiu al lui k
- Dacă angajatul k nu participă la petrecere, atunci subordonații săi direcți pot să participe sau nu la petrecere, după cum este mai avantajos, și obținem relația:
- , j fiu al lui k
Problema care se pune acum este cum să facem parcurgerea arborelui într-un mod cât mai avantajos. Pseudocodul (recursiv) sub forma sa cea mai generală este:
procedura Calcul(k, P, Q)
P ← S(k), Q ← 0
pentru fiecare fiu j al lui k:
Calcul(j, P1, Q1)
P ← P + Q1
Q ← Q + max (P1, Q1)
intoarce P,Q
Soluția „de bun simț” este de a construi arborele alocat dinamic. Ar apărea însă o sumedenie de dificultăți. În primul rând, arborele este general, deci nu se cunoaște numărul maxim de fii pe care îi poate avea un nod (pe cazul cel mai defavorabil, rădăcina poate avea N-1 fii). Aceasta înseamnă că legătura trebuie să fie de tip tata (fiecare nod pointează la tatăl său), ceea ce complică procedura de parcurgere: nu se poate apela procedura recursiv, dintr-un nod pentru toți fiii săi, deoarece nu se cunosc fiii, ci numai tatăl! O altă modalitate de alocare a arborelui ar fi cu doi pointeri pentru fiecare nod: unul către primul său fiu și unul către fratele său din dreapta (exemplul din enunț are reprezentate grafic mai jos cele două metode de construcție).
Probabil că veți fi de acord cu mine că e riscant să te aventurezi la o asemenea implementare în timp de concurs, deoarece lucrul cu pointeri presupune o atenție deosebită. Greșelile sunt mai greu de observat și de multe ori duc la blocarea calculatorului, care trebuie resetat mereu, pierzându-se astfel o mulțime de timp. Trebuie deci căutată o metodă de parcurgere a arborelui care să nu necesite o alocare dinamică a memoriei. Putem încerca astfel: inițial P(i)=S(i) și Q(i)=0 pentru orice nod. Urmează acum să tratăm pe rând fiecare nod. Cum ? Știm că pentru fiecare nod k, numerele P(k) și Q(k) intervin în expresia lui P(T(k)) și Q(T(k)). Uitându-ne la formulele de mai sus, observăm că tot ce avem de făcut este să incrementăm P(T(k)) cu Q(k) și Q(T(k)) cu max{P(k),Q(k)}.
Există o singură problemă: Pentru a putea folosi numerele P(k) și Q(k) trebuie să ne asigurăm că ele au fost deja calculate corect, în funcție de caracteristicile tuturor fiilor lui k. În cazul frunzelor, problema este rezolvată, deoarece ele nu au fii. Pentru nodurile interne, este necesar să știm câți fii au ele și câți din aceștia au fost tratați. În momentul în care toți fiii unui nod au fost tratați, poate fi tratat și nodul în sine. În program, vectorul F reține numărul de fiii netratați ai fiecărui nod. La tratarea unui nod k se face decrementarea lui F(T(k)). Un nod k poate fi ales spre tratare dacă F(k)=0. Se observă că formatul datelor de intrare permite cu ușurință construcția vectorului F (numărul de fii al lui k este egal cu numărul de apariții al lui k în vectorul T).
Un algoritm mai ușor de implementat ar fi:
numara fiii fiecarui nod
repeta de N-1 ori:
cauta un nod k cu F(k)=0
P(T(k)) ← P(T(k))+Q(k)
Q(T(K)) ← Q(T(K))+max{P(k),Q(k)}
F(T(K)) ← F(T(K))-1
scrie P(R)
Partea delicată a acestui algoritm este căutarea unui nod k cu F(k)=0. Dacă ea se face secvențial, pornind de fiecare dată de la primul nod și cercetând fiecare element, programul care rezultă are complexitatea . Această căutare trebuie deci optimizată, și iată cum: În principiu, putem căuta nodurile cu F(k)=0 mergând numai în sensul crescător al indicilor în vector. Vom folosi, ca și la problema codului lui Pruffer, două variabile: K și Next. K este nodul tratat în prezent, iar Next este nodul care urmează a fi tratat la pasul următor, așadar Next > K. După tratarea nodului K și decrementarea lui F(T(k)), pot surveni trei situații:
- F(T(k))>0 și în vectorul F nu a apărut nici un alt element zero, caz în care nimic nu se schimbă, algoritmul continuând cu tratarea nodului Next;
- F(T(k))=0 și T(k)>Next, caz în care de asemenea se poate trata nodul Next (deoarece selectarea nodurilor cu F(k)=0 se face în ordine crescătoare a indicilor);
- F(T(k))=0 și T(k)<Next, caz în care se va trata mai întâi nodul T(k), urmând a se reveni apoi la nodul Next.
Pentru motivele explicate la codul lui Pruffer, acest algoritm nu necesită menținerea unei stive, iar timpul total de căutare este . Facem observația că nu se poate găsi un algoritm mai bun, deoarece trebuie parcurse toate cele N noduri ale arborelui.
Iată în încheiere cum arată arborele cu valorile P și Q atașate fiecărui nod:
#include <stdio.h>
#define NMax 1000
typedef long Vector[NMax+1];
Vector T,S,P,Q,F; /* T = Vectorul de tati,
S = sociabilitatile,
P,Q = caracteristicile,
F = numarul de fii */
int N,Root;
void InitData(void)
{ int i;
FILE *InF=fopen("input.txt","rt");
fscanf(InF,"%d",&N);
for (i=1;i<=N+1;F[i++]=0);
for (i=1;i<=N;i++)
{ fscanf(InF,"%d",&T[i]);
if (T[i]) F[T[i]]++; else Root=i;
}
for (i=1;i<=N;i++) fscanf(InF,"%d",&S[i]);
fclose(InF);
for (i=1;i<=N;P[i++]=S[i]);
for (i=1;i<=N;Q[i++]=0);
}
void FindNext(int *K,int *Next)
{ F[T[*K]]--;
F[*K]=-1;
if ((F[T[*K]]>0) || (T[*K]>*Next))
{ *K=*Next;
while (F[*Next]) (*Next)++;
}
else *K=T[*K];
}
void TraverseTree(void)
{ int K=0,Next,i;
do; while (F[++K]);
Next=K; do; while (F[++Next]);
for (i=1;i<N;i++)
{ P[T[K]]+=Q[K];
Q[T[K]]+=(P[K]>Q[K]) ? P[K] : Q[K];
FindNext(&K,&Next);
}
}
void main(void)
{
InitData();
TraverseTree();
printf("%ld\n",P[Root]);
}
Problema 10
Această problemă a fost dată la unul din barajele pentru selecționarea lotului restrâns al României pentru Olimpiada Internațională din 1996.
ENUNȚ: Fie un număr prim P. Pe mulțimea {0, 1, ..., P-1} se definesc operațiile binare +, -, ×, / modulo P, în felul următor:
- a+b modulo P este restul împărțirii lui a+b la P. Analog pentru '×'.
- Expresia a-b este definită ca fiind soluția ecuației . Analog pentru '/'.
Se știe că ecuația are întotdeauna soluție unică, iar are soluție unică pentru orice b ≠ 0. Pentru b = 0, operația a/b nu e definită. De exemplu, dacă P=11, atunci 6+7=2, 6-7=10, 6*7=9, 6/7=4. Se știe că adunarea și înmulțirea modulo P sunt comutative, asociative, posedă elemente neutre (pe 0, respectiv pe 1), iar adunarea este distributivă față de înmulțire. În plus, pentru orice a există b astfel încât a+b=0; notând b cu (-a) avem c-a=c+(-a)=c+b pentru orice c. De asemenea, pentru orice a ≠ 0 există b astfel încât a × b=1; notând b cu (1/a) avem că c/a=c(1/a)=c × b.
Dându-se un număr prim P, un întreg D între 0 și P-1 și un șir de N numere, cuprinse fiecare între 0 și P-1, se cere să se introducă între elementele șirului operatorii +, -, ×, / și parantezele corespunzătoare, astfel încât să se obțină o expresie corectă a cărei valoare să fie D (lucrând în aritmetica modulo P). În caz că acest lucru nu este posibil, se va afișa un mesaj corespunzător.
Intrarea: Fișierul INPUT.TXT conține două linii:
- pe prima linie se găsesc trei numere întregi: P, N și D, separate prin spații (2≤P≤ 23, P prim, 1 ≤ N ≤ 30, 0 ≤ D ≤ P-1);
- pe următoarea linie se găsește șirul de numere ce formează expresia (N numere întregi cuprinse între 0 și P-1).
Ieșirea: Fișierul text OUTPUT.TXT va conține o singură linie pe care se va găsi expresia generată sau mesajul „Nu există soluție.”. Expresia va fi parantezată complet (fiecare operator va avea o pereche de paranteze atașate).
Exemple:
| INPUT.TXT | OUTPUT.TXT |
|---|---|
| 11 3 6 4 7 9 |
(4+(7/9)) |
| 11 3 7 1 1 1 |
Nu exista solutie. |
Timp de execuție pentru un test: 1 minut.
Modificările și completările propuse de autor sunt:
- Timp de execuție: 10 secunde
- Timp de implementare: 1h 30 minute, maxim 1h 45 minute.
- Complexitate cerută: .
REZOLVARE: Problema în sine nu este foarte complicată. Ea face apel la programarea dinamică, dar este foarte asemănătoare cu una din problemele bine cunoscute de elevi - înmulțirea optimă a unui șir de matrice. Ceea ce o face mai „provocatoare” este timpul alocat implementării. De fapt, la respectiva probă au fost propuse trei probleme, cam de același nivel de dificultate, iar timpul total permis a fost de 4 ore. De asemenea, structurile de date impuse și modul de utilizare a lor sunt mai rar întâlnite.
Ideea de la care se pornește în rezolvarea acestei probleme este următoarea: Parantezarea și completarea cu operatori a unui șir de N numere, V=(V(1), V(2), ..., V(N)), astfel încât să se obțină rezultatul D este posibilă dacă și numai dacă există două valori și , un număr întreg K cuprins între 1 și N-1 și un operator astfel încât următoarele condiții să fie îndeplinite simultan:
- Este posibilă parantezarea și completarea cu operatori a șirului V’=(V(1), V(2), ..., V(K)) astfel încât să se obțină rezultatul ;
- Este posibilă parantezarea și completarea cu operatori a șirului V’’=(V(K+1), V(K+2), ..., V(N)) astfel încât să se obțină rezultatul ;
Cu alte cuvinte, trebuie să găsim un loc în care să „spargem” expresia noastră în așa fel încât, luând două valori care se pot obține pentru partea din stânga, respectiv din dreapta, și inserând între ele operatorul potrivit, să obținem valoarea D.
Pentru aflarea operatorului, a locului de împărțire a expresiei în două și a celor două valori necesare, ar fi de ajuns patru instrucțiuni repetitive for. Totuși, rămâne o singură întrebare: cum se poate verifica dacă se poate sau nu obține valoarea pentru subexpresia din stânga, respectiv valoarea pentru subexpresia din dreapta? Aceasta este o subproblemă similară cu problema în sine, dar redusă la dimensiuni mai mici. O abordare directă ar fi comodă: se scrie o procedură care efectuează cele patru instrucțiuni for și, pentru fiecare combinație posibilă de operatori și operanzi, se reapelează recursiv ca să afle dacă valorile operanzilor se pot obține. Totuși, este intuitiv că această variantă va avea o complexitate uriașă, care o face inutilizabilă.
Motivul principal al nerentabilității acestei implementări este că ea reface de nenumărate ori exact aceleași calcule. Spre exemplu, dacă N=4, programul va încerca să spargă vectorul (V(1), V(2), V(3), V(4)) în două părți. Există trei moduri posibile:
- (V(1)) și (V(2), V(3), V(4)); (a)
- (V(1), V(2)) și (V(3), V(4)); (b)
- (V(1), V(2), V(3)) și (V(4)); (c)
Pentru a studia cazul (c), expresia stângă va trebui la rândul ei ruptă în două bucăți, lucru care poate fi făcut în două moduri:
- (V(1)) și (V(2), V(3)); (d)
- (V(1), V(2)) și (V(3)); (e)
Se observă că deja secvența (V(1), V(2)) a fost studiată de două ori (în cazurile (b) și (e)), iar secvența (V(1)) tot de două ori (în cazurile (a) și (d)). Exemplele pot continua. Dacă însă am reuși să nu mai evaluăm de două ori aceeași secvență, complexitatea programului s-ar reduce foarte mult. Pentru aceasta, trebuie să pornim cu secvențe foarte scurte (întâi cele de un singur număr, apoi cele de două numere), și să trecem la secvențe mai lungi, bazându-ne pe faptul că secvențele mai lungi se descompun în secvențe mai scurte care au fost deja analizate. Facem mențiunea că o secvență cu un singur număr poate fi parantezată într-un singur fel (practic nu este nevoie de paranteze și operatori) și poate produce un singur rezultat, egal cu valoarea numărului. O secvență de două numere poate produce maxim patru rezultate distincte, prin folosirea pe rând a celor patru operatori disponibili.
Pentru a stoca rezultatele obținute, vom folosi o matrice tridimensională A de dimensiuni NxNxP. A[i,j,r] indică dacă există vreo parantezare corespunzătoare a secvenței (V(i), V(i+1), ..., V(j)) astfel încât să se obțină rezultatul r. Dacă o asemenea parantezare există, A[i,j,r] va indica punctul în care trebuie spartă în două expresia (printr-un număr între i și j-1). Dacă nu există o asemenea parantezare, A[i,j,r] va lua o valoare specială (0 de exemplu).
De aici decurge modul de inițializare al matricei:
- A[i,i,V(i)]=i, ∀ 1 ≤ i ≤ N
- A[i,j,r]=0, pentru orice alte valori ale lui i, j și r
Matricea se va completa pe diagonală, începând de la diagonala principală și terminând în colțul de NE. Pentru a afla toate valorile care se pot obține prin parantezarea secvenței (V(i), V(i+1), ..., V(j)), se va împărți această expresie în două părți disjuncte, în toate modurile posibile: (V(i)) și (V(i+1), ..., V(j)), apoi (V(i), V(i+1)) și (V(i+2), ..., V(j)) și așa mai departe până la (V(i), V(i+1), ..., V(j-1)) și (V(j)). Fiecăreia din părțile obținute îi va corespunde în matrice un element de forma A[i,k] sau A[k+1,j], cu i ≤ k < j. În orice caz, toate elementele de această formă se vor afla în matrice dedesubtul diagonalei din care face parte elementul A[i,j], deci pentru secvențele respective se cunosc deja toate valorile pe care le pot lua prin parantezare și introducerea operatorilor. Tot ce avem de făcut este să combinăm în toate modurile aceste valori prin inserarea fiecăruia din cei patru operatori pentru a obține toate valorile posibile ale expresiei (V(i), V(i+1), ..., V(j)).
Dacă în final A[1,N,D]<>0, atunci problema are soluție. Vom vedea imediat și cum se reconstituie ea. Iată modul de compunere a matricei pentru exemplul din enunț (cu deosebirea că, în figurile de mai jos, A[i,j] nu mai este un vector cu P elemente, ci o mulțime de valori între 0 și P-1, această reprezentare fiind mai comodă):
Între numerele 4 și 7 plasăm cei patru operatori și obținem:
Analog se procedează pentru numerele 7 și 9:
Pentru a calcula A[1,3], putem grupa termenii în două moduri: Fie primul separat și ultimii doi separat, fie primii doi separat și ultimul separat. În primul caz, ultimii doi termeni - după cum s-a văzut - pot produce patru rezultate distincte (2, 5, 8 și 9). Combinând oricare din aceste rezultate cu primul termen (4) și adăugând orice operator, vor rezulta 16 valori posibile, din care evident unele vor coincide. Analog se procedează și pentru celălalt caz:
| Cazul I | Cazul II |
|---|---|
Se observă că singura valoare care nu se poate obține prin parantezarea șirului (4, 7, 9) este 5. Să vedem acum și care este metoda de reconstituire a soluției. Fie A[1,N,D]=X. Dacă X=0, atunci nu există soluție. Dacă X ≠ 0, atunci X indică poziția din vector după care trebuie inserat semnul. Nu se indică însă ce semn trebuie inserat, nici care sunt valorile care trebuie obținute pentru partea stângă, respectiv dreaptă. De aceea, vom căuta o combinație oarecare de valori și care se pot obține și un operator oarecare astfel încât . Odată ce le găsim, vom căuta, prin aceeași metodă, o modalitate de a obține valoarea în partea stângă a vectorului (știm sigur că această modalitate există) și o modalitate de a obține valoarea în partea dreaptă a vectorului.
Iată în continuare câteva detalii de implementare. Pentru efectuarea operațiilor matematice modulo P s-a scris o funcție separată, Expr, care primește două numere X și Y între 0 și P-1 și un număr Op între 1 și 4 reprezentând codificarea operatorului și întoarce un număr între 0 și P, reprezentând valoarea operației (X Op Y). De fapt, ar trebui ca această funcție să întoarcă un număr între 0 și P-1 dacă operația este posibilă și să nu întoarcă nimic dacă operația este imposibilă, respectiv dacă se încearcă o împărțire la 0. Cum acest lucru nu este posibil în Pascal, am asimilat valoarea P cu un cod de eroare, iar funcția va întoarce această valoare (care nu poate fi atinsă prin operații obișnuite) în cazul unei împărțiri prin 0. Mai departe, pentru a nu face un test separat dacă rezultatul funcției reprezintă o adresă valabilă în cea de-a treia dimensiune a tabloului, am preferat să supradimensionăm tabloul cu o unitate și să ignorăm tot ceea ce se scrie în coloana P.
Să ne ocupăm acum de operațiile aritmetice. Adunarea, scăderea și înmulțirea se fac în timp constant. O problemă apare în cazul împărțirii, deoarece ea nu mai seamănă deloc cu cea învățată pe mulțimea . Pentru a calcula X/Y, trebuie găsit acel număr Z care, înmulțit cu Y, să dea X. Acest lucru se poate face într-o primă fază prin căutare secvențială (se încearcă valoarea 0, apoi 1, apoi 2 și așa mai departe; trebuie să existe un cât deoarece P este prim). Tehnica are însă influențe neplăcute asupra complexității, supărătoare asupra timpului de rulare și dezastruoase asupra punctajului obținut. De aceea, este bine ca, în măsura în care timpul o permite, să se construiască o tabelă predefinită de calculare a inverșilor. Atunci, în loc să se efectueze împărțirea X/Y, se efectuează înmulțirea . Inversul unui element depinde și de modulul ales. Programul care urmează construiește un tabel care a fost importat în programul sursă ca o constantă, matricea Invers (Invers[A,B] este inversul lui B modulo A). Liniile corespunzătoare unor numere neprime au fost totuși inserate, pentru ușurința implementării.
program Invert;
const NMax=30;
PMax=23;
var i,P:Integer;
function Invers(P,K:Integer):Integer;
var i:Integer;
begin
i:=0;
repeat Inc(i) until (K*i) mod P=1;
Invers:=i;
end;
begin
Assign(Output,'invers.txt');Rewrite(Output);
for P:=2 to PMax do
begin
Write('{',P:2,'} (');
for i:=1 to NMax do
begin
if (P in [2,3,5,7,11,13,17,19,23]) and (i<P)
then Write(Invers(P,i):2)
else Write(99);
if i<>NMax then Write(',');
if i=NMax div 2 then Write(#13#10' ');
end;
WriteLn('),');
end;
Close(Output);
end.Să analizăm în sfârșit complexitatea: Trebuie completată o matrice, deci elemente. Pentru fiecare element din matrice, secvența corespunzătoare din vector trebuie spartă în două în toate modurile posibile, deci încă . Pentru fiecare descompunere, trebuie combinate în toate felurile toate valorile disponibile pentru partea stângă, respectiv dreaptă. Cum numărul de valori este , rezultă o complexitate de . Înmulțind toți acești factori rezultă o complexitate totală de . Dacă nu am fi făcut împărțirea a două numere modulo P în timp constant, ci în , atunci complexitatea totală ar fi fost , deci timpul de rulare putea fi și de 20 de ori mai mare.
Programul de mai jos pare îngrozitor de lung, dar, dacă avem în vedere faptul că o bună bucată o reprezintă constanta Invers, care este generată, putem avea speranțe să-l scriem în timpul alocat.
program ParaNT;
{$B-,I-,R-,S-}
const NMax=30;
PMax=23;
NoWay=0;
OpNames:String[4]='+-*/';
Invers:array[2..PMax,1..NMax] of Integer=
{ 2}(( 1,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{ 3} ( 1, 2,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{ 4} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{ 5} ( 1, 3, 2, 4,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{ 6} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{ 7} ( 1, 4, 5, 2, 3, 6,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{ 8} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{ 9} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{10} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{11} ( 1, 6, 4, 3, 9, 2, 8, 7, 5,10,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{12} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{13} ( 1, 7, 9,10, 8,11, 2, 5, 3, 4, 6,12,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{14} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{15} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{16} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{17} ( 1, 9, 6,13, 7, 3, 5,15, 2,12,14,10, 4,11, 8,
16,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{18} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{19} ( 1,10,13, 5, 4,16,11,12,17, 2, 7, 8, 3,15,14,
6, 9,18,99,99,99,99,99,99,99,99,99,99,99,99),
{20} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{21} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{22} (99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,
99,99,99,99,99,99,99,99,99,99,99,99,99,99,99),
{23} ( 1,12, 8, 6,14, 4,10, 3,18, 7,21, 2,16, 5,20,
13,19, 9,17,15,11,22,99,99,99,99,99,99,99,99));
type Matrix=array[1..NMax, 1..NMax, 0..PMax] of Integer;
{ S-a inclus si valoarea PMax, care nu poate fi
atinsa, pentru a se depozita "deseurile" }
Vector=array[1..NMax] of Integer;
var A:Matrix; { Matricea de calcul }
V:Vector; { Numerele }
N,P,D:Integer;
procedure ReadData;
var i:Integer;
begin
Assign(Input,'input.txt');Reset(Input);
ReadLn(P,N,D);
for i:=1 to N do Read(V[i]);
Close(Input);
end;
function Expr(X,Y,Op:Integer):Integer;
{ Calculeaza expresia (X Op Y) unde Op=1 ('+'),
Op=2 ('-'), Op=3 ('*'), Op=4 ('/'). Daca Op=4
si Y=0 se returneaza valoarea P (care nu poate
fi atinsa prin alte operatii corecte). }
begin
case Op of
1:Expr:=(X+Y) mod P;
2:Expr:=(X+P-Y) mod P;
3:Expr:=(X*Y) mod P;
4:if Y=0 then Expr:=P { = imposibil }
else Expr:=(X*Invers[P,Y]) mod P
{ S-a creat o tabela predefinita de inversi,
deoarece altfel impartirea se efectua numai
in O(P) }
end; {case}
end;
procedure Combine(i,j,k:Integer);
{ Urmeaza a se combina toate valorile posibile
pentru A[i,k] si A[k+1,j] pentru a se afla
toate valorile posibile pentru A[i,j] }
var p1,p2,Op:Integer;
begin
for p1:=0 to P-1 do
if A[i,k,p1]<>NoWay
then for p2:=0 to P-1 do
if A[k+1,j,p2]<>NoWay
then { Am gasit doua valori posibile
si aplicam cei patru operatori }
for Op:=1 to 4 do
A[i,j,Expr(p1,p2,Op)]:=k;
end;
procedure ComposeMatrix;
var i,j,k,l:Integer;
begin
{ Initializarea matricei }
for i:=1 to N do
for j:=1 to N do
for k:=0 to P-1 do A[i,j,P]:=NoWay;
for i:=1 to N do
A[i,i,V[i]]:=1; { sau orice <> NoWay }
for l:=2 to N do { Lungimea intervalelor }
for i:=1 to N-l+1 do
begin
j:=i+l-1; { S-au fixat [i,j] capetele intervalului }
for k:=i to j-1 do { Se alege locul de impartire }
Combine(i,j,k);
end;
end;
procedure SeekValues(Lo,Hi,Mid,Value:Integer;
var v1,v2:Integer; var Op:Char);
{ Se stie unde e "sparta" expresia in doua; se cauta
valorile care trebuie obtinute pentru partea stanga,
respectiv dreapta, si pentru operator }
var i,j,k:Integer;
begin
for i:=0 to P-1 do
if A[Lo,Mid,i]<>NoWay
then for j:=0 to P-1 do
if A[Mid+1,Hi,j]<>NoWay
then for k:=1 to 4 do
if Expr(i,j,k)=Value
then begin
v1:=i;
v2:=j;
Op:=OpNames[k];
Exit;
end;
end;
procedure WriteExpression(Lo,Hi,Value:Integer);
var v1,v2,Place:Integer;
Op:Char;
begin
if Lo=Hi
then Write(V[Lo])
else begin
Place:=A[Lo,Hi,Value];
SeekValues(Lo,Hi,Place,Value,v1,v2,Op);
Write('(');
WriteExpression(Lo,Place,v1);
Write(Op);
WriteExpression(Place+1,Hi,v2);
Write(')');
end;
end;
procedure WriteSolution;
begin
Assign(Output,'output.txt');Rewrite(Output);
if A[1,N,D]=NoWay
then Write('Nu exista solutie')
else WriteExpression(1,N,D);
WriteLn;
Close(Output);
end;
begin
ReadData;
ComposeMatrix;
WriteSolution;
end.O posibilă îmbunătățire a programului de sus ar fi să reținem în A[i,j,r] nu numai locul unde se face secționarea expresiei, ci și operatorul introdus și eventual și valorile care trebuie obținute pe partea stângă, respectiv dreaptă. Totuși, volumul de date ar fi crescut corespunzător și ar fi devenit greu de manipulat. În schimb, în versiunea prezentă, programul merge puțin mai lent, dar nesesizabil. Să vedem de ce. Complexitatea reconstituirii expresiei în sine se află astfel: avem de reconstituit operatori. Pentru fiecare din ei, trebuie să căutăm valorile stângă și dreaptă și operatorul în sine, deci . Complexitatea totală a reconstituirii datelor este , adică oricum mult mai mică față de cea a compunerii matricei. Este preferabil să nu complicăm structurile de date și codul scris, mai ales că diferența ca timp de rulare este infimă.
Propunem ca temă cititorului o versiune a acestei probleme, în care nu se va mai lucra în inelul , ci într-un grup cu elementele a, b, c, d, ..., pentru care se cunoaște tabela de compoziție. În acest caz avem un singur operator , iar cerința este să se parantezeze expresia astfel încât rezultatul să fie y.
Problema 11
Problema celui mai lung prefix a fost dată la a VIII-a Olimpiadă Internațională de Informatică, Veszprem 1996. Iată enunțul nemodificat al problemei:
ENUNȚ: Structura unor compuși biologici este reprezentată prin succesiunea constituenților lor. Acești constituenți sunt notați cu litere mari. Biologii sunt interesați să descompună o secvență lungă în altele mai scurte, numite primitive. Spunem că o secvență S poate fi compusă dintr-un set de primitive P dacă există N primitive p1, ..., pN în P astfel încât concatenarea p1p2...pN a primitivelor să fie egală cu S. Aceeași primitivă poate interveni de mai multe ori în concatenare și nu trebuie neapărat ca toate primitivele să fie prezente.
Primele M caractere din S se numesc prefixul lui S de lungime M. Scrieți un program care primește la intrare un set de primitive P și o secvență de constituenți T. Programul trebuie sa afle lungimea celui mai lung prefix al lui T care se poate compune din primitive din P.
Datele de intrare apar în două fișiere. Fișierul INPUT.TXT descrie setul de primitive P, iar fișierul DATA.TXT conține secvența de examinat. Pe prima linie din INPUT.TXT se află N, numărul de primitive din P (1 ≤ N ≤ 100). Fiecare primitivă se dă pe două linii consecutive: pe prima lungimea L a primitivei (1 ≤ L ≤ 20), iar pe a doua un șir de litere mari de lungime L. Toate cele N primitive sunt distincte.
Fiecare linie din fișierul DATA.TXT conține o literă mare pe prima poziție. El se termină cu o linie conținând un punct ('.'). Lungimea secvenței este cuprinsă între 1 si 500.000.
Ieșirea: Pe ecran se va tipări lungimea celui mai lung prefix din T care poate fi compus din primitive din P.
Exemplu:
| INPUT.TXT | OUTPUT.TXT |
|---|---|
| 5 1 |
A B |
Pe ecran se va tipări numărul 11.
Timp de rulare: 30 secunde pentru un test.
Timp de implementare: 1h.
Complexitate cerută: , unde S este lungimea secvenței.
REZOLVARE: Menționăm de la început că datele problemei sunt supradimensionate. Nici unul din cele zece teste cu care au fost verificate programele nu a depășit în realitate 12 primitive. În schimb, fișierul DATA.TXT a fost unic pentru toate testele și a conținut o secvență de lungime 500.000.
Problema se rezolvă și în acest caz prin reducerea ei la una similară, dar cu date de intrare mai mici. Respectiv, un prefix S al lui T se poate descompune în primitive dacă există o primitivă astfel încât și S’ se poate descompune în primitive. Am redus împărțirea în primitive a lui S la despărțirea în primitive a lui S’, care are o lungime mai mică decât S. O primă modalitate, pur teoretică, de a rezolva problema, este să reținem toate prefixele lui T care se pot descompune în primitive; în felul acesta, putem studia prefixe din ce în ce mai lungi, bazându-ne pe prefixe mai scurte deja studiate. Totuși, este imposibil să ținem minte toate prefixele lui T, deoarece lungimea medie a unui prefix poate atinge 250.000 caractere.
O îmbunătățire care poate fi adusă acestui algoritm este următoarea: deoarece toate prefixele aparțin aceleiași secvențe de constituenți, T, este suficient să reținem în întregime secvența T și, pentru fiecare prefix ce se poate descompune în primitive, păstrăm doar lungimea sa. Făcând abstracție de limitările de memorie, putem crea un vector V cu S variabile booleene (unde S≤500.000), iar V[i] va indica dacă subșirul de lungime i din T se poate descompune în primitive. V[i] va primi valoarea True dacă și numai dacă există o primitivă p în P de lungime L astfel încât să fie îndeplinite simultan condițiile:
- V[i-L]=True;
- secvența de caractere T[i-L+1]T[i-L+2]...T[i] este egală cu p.
Iată o primă variantă (în pseudocod) a algoritmului:
citeste primitivele
citeste T
pentru i de la 1 la S
daca exista o primitiva p astfel incat
V[i-L] si T[i-L+1]T[i-L+2]...T[i]=p
atunci V[i]←True
altfel V[i]←False
cauta cel mai mare i pentru care V[i]=True
scrie i
Chiar și în acest caz, apare o problemă, deoarece avem nevoie de doi vectori, unul de caractere și altul de variabile booleene, ambii de lungime maxim 500.000. Necesarul de memorie este deci cam de 1MB. Sigur, pentru calculatoarele de astăzi această sumă este ușor de alocat, dar problema admite oricum o soluție la fel de rapidă și mult mai economică. Iată care este principiul:
Pentru a vedea dacă un prefix S de lungime L se poate descompune în primitive, noi avem nevoie să cunoaștem dacă prefixele de lungime mai mică se pot descompune. Dar avem oare nevoie de toate prefixele? Nu, deoarece noi vom concatena unul din prefixele de lungime mai mică cu o primitivă pentru a obține noul prefix S. Însă primitivele au lungime de maxim 20 caractere. Așadar, noi nu trebuie să cunoaștem decât dacă prefixele de lungime L-1, L-2, ..., L-20 se pot descompune; restul nu ne interesează. În felul acesta am eliminat vectorul V și l-am redus la un vector de numai 20 de elemente (care în program se numește CanGet). La fiecare moment, când se prelucrează un nou caracter din secvența de constituenți T, primul element din CanGet se pierde (deoarece informația pe care el o stochează este învechită), iar următoarele 19 elemente se deplasează spre stânga cu câte o poziție. Al 20-lea element, care acum a rămas disponibil, va fi calculat la pasul curent.
O altă modificare pornește de la observația că, datorită aceleiași limitări a lungimii primitivelor la 20 de caractere, nu avem nevoie nici măcar să reținem întregul vector T, ci numai ultimele 20 de litere ale lui. La fiecare pas, litera cea mai „veche” din T (adică de indice minim) se va pierde, iar la celelalte 19 litere se va adăuga litera nou citită. Avem așadar nevoie doar de un string de 20 de caractere, pe care în program l-am numit Last. Pentru a deplasa spre stânga vectorii CanGet și Last, se pot folosi fie atribuirile succesive, fie rutinele de acces direct la memorie.
Deoarece prefixele care se pot descompune sunt identificate în ordinea crescătoare a lungimii, ultimul asemenea prefix găsit este tocmai cel de lungime maximă. Dar pentru că, în momentul în care găsim un prefix, nu putem ști dinainte că el este ultimul, trebuie să reținem într-o variabilă lungimea celui mai lung prefix găsit până la momentul respectiv, variabilă pe care o actualizăm de fiecare dată când găsim un nou prefix.
În felul acesta, am reușit să reducem memoria folosită aproape la strictul necesar, adică numai la dicționarul de primitive și la doi vectori de câte douăzeci de caractere. Se recomandă totuși să se aloce un buffer cât mai mare pentru citirea datelor din fișierul DATA.TXT pentru mărirea vitezei de citire. Repartizarea buffer-ului se face cu procedura Pascal SetTextBuf.
O optimizare care nu a fost inclusă în program, fiind lăsată ca temă cititorului, este următoarea: dacă la un moment dat, în timpul examinării secvenței de constituenți, este întâlnit un șir de cel puțin 20 de prefixe consecutive, din care nici unul nu se poate descompune în primitive, atunci nici mai departe nu vom mai întâlni vreun prefix care să se poată descompune. Explicați de ce. Această optimizare poate să nu aducă uneori nimic nou în evoluția programului, dar alteori poate să reducă la zero timpul de rulare.
Prezentăm mai jos codul sursă al programului. A fost preferat limbajul Pascal, deoarece pune la dispoziție rutine mai comode de manevrare a șirurilor de caractere.
program LongestPrefix;
{$B-,D-,I-,R-,S-}
const NMax=100;
LMax=20;
type Str20=String[LMax+1];
LexType=array[1..NMax] of Str20;
BooleanVector=array[1..LMax+1] of Boolean;
BufferType=array[1..62000] of Byte;
var Lex:LexType; { Dictionarul de primitive }
N:Integer; { Numarul de primitive }
Biggest:LongInt; { Lungimea maxima }
Buf:BufferType; { Buffer de intrare }
procedure ReadPrimitives;
var i,Len:Integer;
begin
Assign(Input,'input.txt');
Reset(Input);
ReadLn(N);
for i:=1 to N do
begin
ReadLn(Len);
ReadLn(Lex[i]);
end;
Close(Input);
end;
procedure Decompose;
var Last:Str20; { Ultimele 20 de caractere citite }
CanGet:BooleanVector;
{ CanGet[i] indica daca Last[i] poate fi
ultimul caracter al unei descompuneri }
i,L:Integer;
Current:LongInt; { Lungimea curenta }
begin
Assign(Input,'data.txt');
SetTextBuf(Input,Buf,SizeOf(Buf));
Reset(Input); { Deschide fisierul cu un buffer atasat }
Biggest:=0;
Last[0]:=Chr(LMax+1);
FillChar(Last,LMax,'@');
FillChar(CanGet,LMax,True);
Current:=0; { Deocamdata nu s-a citit nimic }
ReadLn(Last[LMax+1]); { Citeste primul caracter }
repeat
Inc(Current);
i:=0;
{ Cauta o primitiva potrivita }
repeat
Inc(i);
L:=Length(Lex[i]);
CanGet[LMax+1]:=CanGet[LMax+1-L]
and (Copy(Last,LMax+2-L,L)=Lex[i]);
until CanGet[LMax+1] or (i=N);
{ Am gasit o primitiva? }
if CanGet[LMax+1]
then Biggest:=Current;
{ Deplaseaza spre stanga CanGet si Last }
Move(CanGet[2],CanGet[1],LMax);
Move(Last[2],Last[1],LMax);
{ Avanseaza la urmatorul caracter }
ReadLn(Last[LMax+1]);
until Last[LMax+1]='.';
Close(Input);
end;
procedure WriteSolution;
begin
Assign(Output,'output.txt');
Rewrite(Output);
WriteLn(Biggest);
Close(Output);
end;
begin
ReadPrimitives;
Decompose;
WriteSolution;
end.
Problema 12
Această problemă a fost propusă la a IV-a Balcaniadă de Informatică, Nicosia 1996.
ENUNȚ: Grupul de rock U2 va da un concert în Nicosia. Un grup de N ≤ 200 fani U2 așteaptă la coadă în scopul de a cumpăra bilete de la singura caserie deschisă. Fiecare persoană vrea să cumpere numai un bilet, iar casierul poate vinde unei persoane cel mult două bilete.
Casierul folosește T[i] unități de timp pentru a servi al i-lea fan (1 ≤ i ≤ N). Este posibil totuși ca doi fani așezați la coadă unul după altul (de exemplu, al j-lea și al j+1-lea) să convină ca numai unul din ei să rămână la coadă, iar celălalt să plece, dacă timpul R[j] (1 ≤ j ≤ N-1) în care casierul servește al j-lea și al j+1-lea fan este mai mic decât T[j]+T[j+1]. Deci, pentru a minimiza timpul de lucru al casierului, fiecare persoană din coadă încearcă să negocieze cu predecesorul și cu succesorul său, ceea ce va duce în final la o servire mai rapidă.
Fiind date numerele întregi pozitive N, T[i] (1 ≤ i ≤ N) și R[j] (1 ≤ j ≤ N-1), se cere să se minimizeze timpul total al casierului. Acest lucru va fi realizat grupând într-un mod optim perechi de persoane consecutive. Atenție! Nu este necesar ca un anumit fan să se cupleze neapărat cu predecesorul sau cu succesorul său.
Intrarea: În fișierul INPUT.TXT, datele de intrare sunt date pe trei linii:
- prima linie conține numărul întreg N;
- a doua linie conține N întregi: valorile T[i], separate prin câte un spațiu;
- a doua linie conține N-1 întregi: valorile R[j], separate de asemenea prin câte un spațiu;
Ieșirea se va face în fișierul OUTPUT.TXT, astfel:
- prima linie conține un întreg care reprezintă timpul total (minim) al casierului;
- pe fiecare din următoarele linii se află un singur număr sau două numere separate prin caracterul '+'. Mai exact, fiecare linie conține numărul i dacă al i-lea fan este servit singur, sau i+(i+1) dacă cei doi fani sunt serviți ca o pereche.
Exemplu:
| INPUT.TXT | OUTPUT.TXT |
|---|---|
| 7 5 4 3 2 1 4 4 |
14 1 |
Timp de rulare: 15 secunde pentru un test.
Acesta este enunțul în forma lui de la Nicosia. Iată acum și completările „din studio”:
- Numărul de fani este N ≤ 5000;
- Complexitatea cerută este ;
- Timpul de rulare este de o secundă.
REZOLVARE: O primă metodă de rezolvare o vom lăsa în seama cititorului, întrucât ea este foarte asemănătoare cu rezolvarea problemei înmulțirii optime a unui șir de matrice. Ideea de pornire este de a defini o matrice D cu N linii și N coloane, în care D[X,Y] reprezintă timpul minim în care pot fi serviți fanii X, X+1, ..., Y-1, Y. Scopul este de a afla valoarea D[1,N].
După cum se știe, însă, înmulțirea optimă a unui șir de matrice se poate determina în timp . Pentru condițiile inițiale ale problemei (N ≤ 200), metoda se încadrează în timp. Ea putea fi deci folosită la concurs, pe câtă vreme dacă se impun condițiile suplimentare, rezolvarea în timp cubic nu mai dă rezultate. Iată ideea de rezolvare a problemei în timp liniar.
Vom denumi o cuplare de ordin K modul în care primii K fani sunt serviți câte unul sau câte doi. Fiecare cuplare are atașat un cost, respectiv timpul consumat de casier pentru a servi toți fanii. Dintre toate cuplările de ordin K, cele pentru care costul este minim (în cazul general pot fi mai multe) se vor numi cuplări optime de ordinul K. Cerința problemei exprimată cu noua terminologie este: să se găsească o cuplare optimă de ordinul N.
Să presupunem acum că am găsit cumva această cuplare optimă de ordinul N, pe care o vom nota cu . Dacă în această cuplare al K-lea fan este servit de unul singur, atunci modul de servire al primilor K-1 fani reprezintă o cuplare optimă de ordinul K-1, pe care o vom nota cu . Demonstrația nu este grea: dacă fanii 1, 2, ..., K-1 nu ar fi cuplați în mod optim în cadrul lui , atunci ar exista o cuplare a lor de cost mai mic decât . Dar această cuplare mai bună ar putea fi folosită pentru a obține o cuplare mai bună a tuturor celor N fani (servind primii K-1 fani conform cuplării , iar pe ceilalți conform cuplării ). S-ar obține astfel o cuplare de cost mai mic decât , ceea ce este absurd, deoarece am presupus ca fiind optimă.
În mod absolut identic se poate demonstra că dacă este o cuplare optimă de ordinul N în care fanii K și K+1 sunt serviți împreună, atunci modul de servire al primilor K-1 fani reprezintă o cuplare optimă de ordinul K-1. Recunoaștem în aceste afirmații principiul programării dinamice: optimul global presupune optime locale. De aici deducem că, pentru a realiza o cuplare optimă a primilor K fani avem nevoie de câte o cuplare optimă pentru primii K-1 fani, respectiv pentru primii K-2 fani, urmând ca apoi să aflăm care este costul minim al unei cuplări de ordin K, atât în ipoteza că fanul al K-lea este servit singur, cât și în ipoteza că el este servit împreună cu al K-1-lea fan.
Vom crea așadar doi vectori și , ambii cu câte N elemente, în care:
- este timpul minim în care pot fi serviți fanii 1, 2, ..., K, astfel încât fanul al K-lea să rămână singur;
- este timpul minim în care pot fi serviți fanii 1, 2, ..., K, astfel încât fanii K și K-1 să fie cuplați.
Datele inițiale pe care le putem trece în cei doi vectori sunt:
- (un singur fan nu poate fi cuplat cu nimeni)
- (dacă al doilea fan rămâne singur, atunci și primul rămâne singur)
Relațiile de recurență se deduc fără prea multă bătaie de cap:
- (dacă fanul K rămâne singur, atunci el este servit în timpul T[K], iar fanul K-1 se va cupla cu K-2 sau va rămâne singur, după cum este mai convenabil);
- (dacă fanul K se cuplează cu K-1, atunci ei sunt serviți în timpul R[K-1], iar fanul K-2 se va cupla cu K-3 sau va rămâne singur, după cum este mai convenabil);
Putem deci să completăm vectorii de la stânga la dreapta. Odată ce am făcut aceasta, costul minim al cuplării de ordinul N este . Pentru a reconstitui și așezarea fanilor, vom proceda recurent, astfel: dacă , înseamnă că este mai avantajos ca fanii N și N-1 să fie cuplați și reluăm reconstituirea pentru fanii 1, 2, ..., N-2. În caz contrar, înseamnă că este mai avantajos ca fanul N să rămână singur și reluăm reconstituirea pentru fanii 1, 2, .., N-1. De exemplu, iată modul în care se completează vectorii și pentru exemplul din enunț:
- Fanii 6 și 7 sunt cuplați. Reconstituim așezarea primilor 5 fani.
- Fanii 4 și 5 sunt cuplați. Reconstituim așezarea primilor 3 fani.
- Fanii 2 și 3 sunt cuplați, iar primul fan este singur.
#include <stdio.h>
#define NMax 5001
typedef unsigned IntVector[NMax];
typedef long LongVector[NMax];
IntVector T, R;
LongVector T1, T2;
int N;
FILE *OutF;
void ReadData(void)
{ FILE *F=fopen("input.txt", "rt");
int i;
fscanf(F,"%d\n", &N);
for (i=1; i<=N;)
fscanf(F,"%d", &T[i++]);
for (i=1; i<N;)
fscanf(F,"%d", &R[i++]);
}
long Min(long X, long Y)
{
return X<Y? X : Y;
}
void Match(void)
{ int i;
T1[1]=T[1]; T2[1]=0xFFFF; /* =Infinit */
T1[2]=T[1]+T[2]; T2[2]=R[1];
for (i=3; i<=N; i++)
{
T1[i]=T[i]+Min(T1[i-1],T2[i-1]);
T2[i]=R[i-1]+Min(T1[i-2],T2[i-2]);
}
}
void GoBack(int K)
{
if (K)
if (T1[K]<T2[K])
{ GoBack(K-1);
fprintf(OutF,"%d\n",K);
}
else { GoBack(K-2);
fprintf(OutF,"%d+%d\n",K-1,K);
}
}
void WriteSolution(void)
{
OutF=fopen("output.txt", "wt");
fprintf(OutF,"%d\n",Min(T1[N],T2[N]));
GoBack(N);
fclose(OutF);
}
void main(void)
{
ReadData();
Match();
WriteSolution();
}
- ↑ Greșeală în original, corect: Prüfer








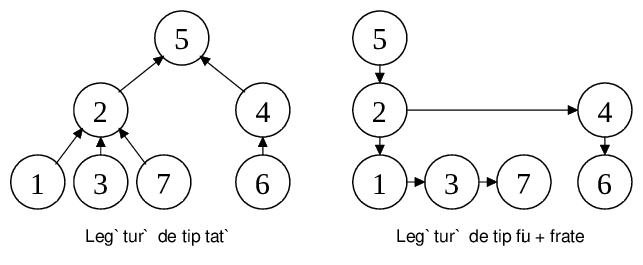
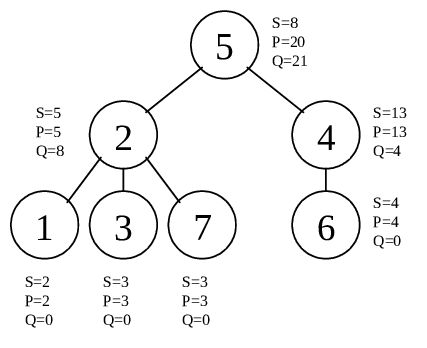








![{\displaystyle A[1,1]=\{4\}\quad A[2,2]=\{7\}\quad A[3,3]=\{9\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3ee4ed115d036e27d01d3e3f704b57d1d17f1c2)

![{\displaystyle {\begin{aligned}4+7&\equiv 0{\pmod {11}}\\4-7&\equiv 4+4\equiv 8{\pmod {11}}\\4\times 7&\equiv 6{\pmod {11}}\\4/7&\equiv 4\times 8\equiv 10{\pmod {11}}\\A[1,2]&=\{0,6,8,10\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e995493fe7fefdcd9b98113584832ece411f5afa)
![{\displaystyle {\begin{aligned}7+9&\equiv 5{\pmod {11}}\\7-9&\equiv 7+2\equiv 9{\pmod {11}}\\7\times 9&\equiv 8{\pmod {11}}\\7/9&\equiv 7\times 5\equiv 2{\pmod {11}}\\A[2,3]&=\{2,5,8,9\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba0cd12b9c415f570c8b2067a0012f6294d37353)









![{\displaystyle A[1,3]=\{0,1,2,3,4,6,7,8,9,10\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13427bb081a9e4733d7c768b706a9a7ce49c9f8d)





















![{\displaystyle T_{1}[K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21730b3e8ca2198ce4a7d4533b7e29fd9deec026)
![{\displaystyle T_{2}[K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15bf16cacf40fdedd4dd88e5c403114222701e32)
![{\displaystyle T_{1}[1]=T[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e0c6903ec75d3a3aece00ab6044f8fb80bea70d)
![{\displaystyle T_{2}[1]=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c92ca034e618115bccf951a114444a0339da167d)
![{\displaystyle T_{1}[2]=T[1]+T[2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce276e51595365e15fcc1212e60408bf51feecb9)
![{\displaystyle T_{2}[2]=R[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/860cfdd12429f8b3e1865f8eddc5e4dcda02a090)
![{\displaystyle T_{1}[K]=T[K]+\min(T_{1}[K-1],T_{2}[K-1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27229dc827d03a5a0c785d848c7de73cdcd1ea14)
![{\displaystyle T_{2}[K]=R[K-1]+\min(T_{1}[K-2],T_{2}[K-2])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/652fe1ef8ee7cfe010382a969dac7ecd62a3666f)
![{\displaystyle \min(T_{1}[N],T_{2}[N])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9935774672a96445b3124631e15a405cd284ef9)
![{\displaystyle T_{2}[N]<T_{1}[N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68a2fe4ccdf41731b079002a62f4e0c530b62062)
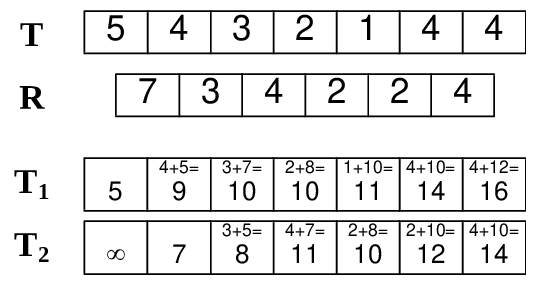
![{\displaystyle T_{2}[7]<T_{1}[7]\implies }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ca1be967cf3a7ff21c09f2957aa635d1e2c93fc)
![{\displaystyle T_{2}[5]<T_{1}[5]\implies }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a06e8ad5282300ea043110337929ea786f70380)
![{\displaystyle T_{2}[3]<T_{1}[3]\implies }](https://wikimedia.org/api/rest_v1/media/math/render/svg/338f944c6f89a7be3167e6a0f54eb4b3115cbb34)