Clasa VII/VIII lecția 27 - 13 mai 2014
Anunț
Concurs: jocul Flood Wars
Scrieți un program care să joace jocul Flood Wars, descris aici:
Concurs Flood Wars 2014, clasele 7/8
Elevii care vor reuși să termine implementarea jocului vor intra în concurs. În cadrul concursului fiecare program va juca cu fiecare alt program două jocuri, unul "tur" și unul "retur".
Mulțumim Andreei Zaharia pentru idee.
Lecție
Precalculare
Precalcularea este un termen general pentru folosirea unor structuri auxiliare de date, fără o legătură directă cu problema de rezolvat, care ne ajută în rezolvarea problemei. Aceste structuri de date sînt calculate la început, ceea ce duce la denumire: precalculare.
În continuare vom vorbi de cîteva exemple clasice de precalculare.
Ciurul lui Eratostene
V-aţi gîndit vreodată că ciurul lui Eratostene este de fapt o precalculare a unui vector de frecvenţă f[], care, pentru fiecare număr p, calculează f[p] care ne spune dacă p este prim? Complexitatea este O(n log log n). Precum vom vedea această precalculare poate fi extinsă să calculeze numărul de divizori ai fiecărui număr din vectorul de frecvență.
Suma între i şi j
În multe probleme apare următoarea subproblemă: avem un vector de n elemente întregi, să se răspundă la multe întrebări de forma care este suma elementelor vectorului între poziţiile i şi j?. În acest caz vom precalcula o structură de date auxiliară, şi anume un vector s, astfel încît s[i] este suma elementelor de la 0 pînă la i. El se mai numeşte şi vectorul sumei prefixelor lui v. Construcția acestui vector se poate face liniar deoarece avem relaţia s[i] = s[i+1] + v[i].
Odată calculat acest vector putem răspunde în timp constant la întrebări. Suma elementelor între i şi j este s[j] - s[i-1]. Memoria folosită este O(n).
Suma între (i, j) şi (ii, jj)
Este problema anterioară extinsă la matrice: avem o matrice de numere întregi şi întrebări de forma: care este suma elementelor matricei în dreptunghiul care are drept colţuri opuse (i1, j1) şi (i2, j2)?. Această problemă apare în problema puncte5 dată la barajul de gimnaziu în 2012. În mod similar vom precalcula o matrice auxiliară cu suma elementelor matricei originale între (0, 0) şi (i, j). Ea poate fi calculată în timp constant per element, astfel:

s[i][j] = s[i][j-1] + s[i-1][j] - s[i-1][j-1] + m[i][j]
Odată calculată matricea s putem răspunde în timp constant la întrebări. Suma elementelor între (i, j) şi (ii, jj) este:
S = s[ii][jj] - s[ii][j-1] - s[i-1][jj] + s[i-1][j-1]

Numărul de biţi 1 într-un întreg
Cum putem calcula numărul de cifre 1 din reprezentarea în baza 2 a unui număr?
- Direct: shift and mask.
- Folosind expresia x & (x - 1).
- Cu precalculare: ţinem un vector în care elementul v[x] este numărul de biţi 1 din reprezentarea în baza 2 a lui x.
- Gîndiţi-vă la un algoritm fără vectori, dar mai rapid decît O(nr. biţi).
Sume de intervale
În lecția 17 am vorbit despre problemele extraterestri si extraterestri1. Aceste probleme cer însumarea unor intervale care au numere asociate. Tot în acea lecție am discutat o rezolvare bazată pe un vector de sume parțiale în care ținem minte pentru fiecare element v[i] numărul care trebuie adunat la fiecare element al vectorului sumă, s[i], începînd cu i pînă la finalul vectorului, astfel încît la final s[] să fie rezultatul căutat.
Acesta este tot un exemplu de precalculare, cunoscut printre voi drept "șmenul lui Mars", denumire care îmi displace deoarece sugerează că informatica este o colecție de șmenuri. Am discutat apoi despre o soluție alternativă, mai generală, care nu folosește precalculare.
Acest tip de precalculare se poate extinde în două dimensiuni, pe matrice. Un exemplu care folosește aceasta este problema flori. Această precalculare necesită O(n2) memorie. Ea nu se justifică decît în măsura în care este facil de programat, deoarece avem o soluție de aceeași complexitate care folosește varianta pe vector, folosind doar O(n) memorie. Acest lucru este exemplificat în problema flori1.
Exemple de probleme cu precalculare
- puncte5: necesită precalcularea sumelor parţiale ale unei matrice.
- paisprezece: necesită precalcularea unui vector al primelor 17 numere prime, precum şi a ciurului lui Eratostene.
- intervale: necesită precalcularea ciurului lui Eratostene precum şi a sumelor parţiale ale numărului de divizori primi.
- reginald, o extindere a problemei anterioare.
- extraterestri precalculare vector sume prefixe parțiale (a.k.a. șmenul lui Mars)
- extraterestri1 Mars + normalizare coordonate
Concluzii
- Precalcularea foloseşte atunci cînd avem de răspuns la mai multe întrebări costisitoare. Aceste întrebări pot fi explicite, cerute de enunţ, sau implicite, decurgînd din metoda de rezolvare, ca la problema puncte5.
- Precalcularea poate folosi şi atunci cînd numărul de întrebări este mult mai mare decît numărul de răspunsuri posibile, caz în care putem precalcula toate răspunsurile într-un tabel înainte de a răspunde la întrebări.
- Precalcularea foloseşte o structură de date adiţională şi memorie suplimentară. Uneori putem economisi memorie folosindu-ne chiar de structura de date iniţială.
Maximum în fereastră glisantă (maximum over a sliding window)
- Enunț: dîndu-se un șir de n numere considerăm cele n – k + 1 subsecvențe de k numere consecutive în șir (denumite și "ferestre" de lungime k). Putem vedea aceste ferestre ca pe o singură fereastră, deplasabilă, care ne dă acces la k elemente din vector odată. Se cere ca pentru fiecare fereastră să se găsească maximul.
- Algoritmul de rezolvare trivial (forță brută) recalculează maximul pentru fiecare din ferestre, avînd complexitate O(kn).
- Pentru a reduce complexitatea găsirii maximului procedăm astfel: luăm prima fereastră, de la 0 la k-1. Să spunem că maximul se află pe poziția p1. Pe măsură ce vom deplasa fereastra este imposibil ca elementele din-naintea maximului să fie vreodată maximul ferestrei, deoarece ele vor face parte împreună cu maximul din această fereastră. Să considerăm poziția celui mai mare element după maxim și la dreapta lui, în fereastră. Fie ea p2. Rezultă că nici un element pe pozițiile intermediare i, p1 < i < p2, nu poate fi vreodată maxim în fereastră, deoarece aceste elemente vor fi împreună cu p2 în toate ferestrele care le conțin. Similar, considerînd p3 poziția următorului maxim, nici un element între p2 și p3 nu va putea fi maxim. Astfel apare următorul algoritm: memorăm toate maximele descrescătoare din prima fereastră, într-o coadă. Primul element din coadă este maximul ferestrei. Cînd deplasăm fereastra trebuie să actualizăm structura de maxime din coadă. Pentru aceasta dăm atenție elementului care dispare din fereastră și celui care intră în fereastră. Dacă elementul care iese nu este maximul curent, nu avem nimic de făcut. Dacă este maximul curent vom scoate primul element din coada de maxime. Dacă elementul proaspăt adăugat în fereastră este mai mic decît ultimul maxim din coadă se adaugă la coadă. În caz contrar el va "arunca" ultimul element, iar apoi încercăm din nou. Rezultă că noul element din fereastră "aruncă" toate elementele de la urma cozii strict mai mic ca el, iar apoi îl adăugăm normal la coadă.
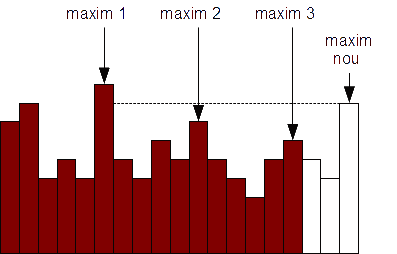
În figură noul maxim va elimina din coadă maximele 2 și 3. Coada rămasă va conține maximul 1 și maximul nou - La prima vedere pare că acest algoritm are complexitate O(kn). Folosind analiza amortizată putem calcula complexitatea reală ca fiind O(n).
- Memoria suplimentară folosită este mărimea maximă a cozii, adică O(k).
- Observăm că putem folosi acest algoritm la problema cuburi. Genul acesta de prelucrare, eliminarea unor cifre ale unui număr astfel încît numărul rămas să fie maxim (sau minim) apare des la olimpiade.
Temă
Rezolvări aici [1]