Clasa VII/VIII lecția 6 - 5 nov 2013
Tema - rezolvări
Rezolvări aici [1]
Lecție
Recursivitate - încheiere
Fill recursiv (flood fill)
Introducere
Algoritmul fill "umple" toate golurile accesibile de la un punct dat. Golurile pot fi elemente zero intr-o matrice, de exemplu, iar vecinii pot fi definiți ca elementele adiacente pe linie și coloană (acesta este cazul cel mai întîlnit). Alteori vecinii pot fi definiți ca avînd un punct comun cu elementul curent, ceea ce include și elementele alăturate pe diagonală. Să luăm un exemplu clasic:
Se dă o matrice a[m][n] cu elemente 0 și 1, 0 semnificînd liber și 1 semnificînd zid, precum și o poziție în matrice, (l, c). Să se spuna cîte elemente 0 sînt accesibile de la (l, c) avansînd doar pe linie sau pe coloană.
int suma;
...
void fill( int l, int c ) {
suma++;
a[l][c] = 1;
if ( l > 0 && a[l-1][c] == 0 )
fill( l - 1, c );
if ( l < m-1 && a[l+1][c] == 0 )
fill( l + 1, c );
if ( c > 0 && a[l][c-1] == 0 )
fill( l, c - 1 );
if ( c < n-1 && a[l][c+1] == 0 )
fill( l, c + 1 );
}
...
int main() {
...
suma = 0;
if ( a[l][c] == 0 )
fill( l, c );
printf( "%d", suma );
...
}
Acest algoritm are complexitate O(m×n) ca timp, deoarece poate parcurge toate elementele matricei, iar prelucrarea per element este O(1). Memoria ocupată este de asemenea O(m×n) deoarece fiecare apel recursiv necesită O(1) memorie și putem avea O(m×n) apeluri recursive unul în altul.
Atenție! Acesta este principalul impediment al metodei! Ea folosește foarte multă memorie suplimentară.
Optimizări
Bordare matrice
O primă optimizare de timp este clasică. Pentru a face programul atît mai rapid cît și mai scurt putem borda matricea de jur împrejur cu elementul zid, în cazul nostru 1. Astfel vom scuti testul de ieșire a coordonatelor din matrice. Funcția se simplifică:
void fill( int l, int c ) {
suma++;
a[l][c] = 1;
if ( a[l-1][c] == 0 )
fill( l - 1, c );
if ( a[l+1][c] == 0 )
fill( l + 1, c );
if ( a[l][c-1] == 0 )
fill( l, c - 1 );
if ( a[l][c+1] == 0 )
fill( l, c + 1 );
}
Reducere memorie folosită
Cum calculăm memoria ocupată? Țineți minte: fiecare apel recursiv ocupă memorie echivalentul unui int. Pe un calculator de 32 de biți, cum sint cele pe care lucrăm noi, aceasta înseamnă patru octeți. Aceasta este adresa de întoarcere din funcție. Alte elemente care ocupă memorie pe stivă sînt parametrii transmiși și variabilele declarate în funcție. În cazul nostru vom avea 8 octeți cei doi parametri.
Dacă micșorarea memoriei folosite este esențială putem elimina acești parametri, făcînd variabilele l și c globale, astfel:
int l, c;
...
void fill() {
suma++;
a[l][c] = 1;
l--;
if ( a[l][c] == 0 )
fill();
l++;
l++;
if ( a[l][c] == 0 )
fill();
l--;
c--;
if ( a[l][c] == 0 )
fill();
c++;
c++;
if ( a[l][c] == 0 )
fill();
c--;
}
Este o modificare urîtă, care face codul nelizibil, dar uneori necesară la olimpiadă. Nu uitați că chiar și în această formă algoritmul va folosi 4 octeți pe apel recursiv imbricat pentru adresa de revenire din funcție.
Aplicații
- Găsire ieșire din labirint: găsirea unui punct (sau tuturor punctelor) de ieșire dintr-un labirint, dacă există.
- Calcul suprafață goluri: acesta este exemplul de mai sus, care numără elementele zero accesibile din punctul inițial.
- Calcul număr de goluri: denumite și componente conexe, putem folosi fill pentru a număra cîte goluri disjuncte există (astfel încît să nu se poată ajunge de la un gol la altul). Pentru aceasta vom parcurge matricea în orice ordine și vom porni cîte un fill din fiecare loc unde găsim un element 0.
Concluzie
Fill este o unealtă simplă și utilă, ușor de folosit la concursuri. Principalul ei neajuns este memoria ocupată. Ce facem în situația cînd matricea este prea mare și memoria disponibilă insuficientă pentru a folosi flood fill? În această situație putem folosi BFS fill (breadth first search), care, atunci cînd este aplicat pe o matrice se mai numește și algoritmul Lee. El folosește o coadă pentru a menține frontiera deja acoperită, reducînd memoria la O(m+n). Vom discuta acest algoritm într-o altă lecție.
Liste
Definiție
Definiție: în informatică o listă înlănțuită este o structură de date care constă dintr-un grup de noduri care împreună reprezintă o secvență. În forma ei cea mai simplă fiecare nod este format din date și o referință (înlănțuire) către nodul următor în secvență. Lista înlănțuită permite inserarea și ștergerea eficientă a elementelor de pe orice poziție în secvență.
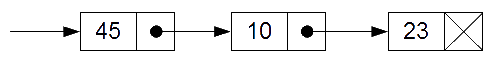
Implementare
O primă implementare posibilă este folosind doi vectori: un vector v care memorează elementele listei (numere întregi de exemplu) și un vector next, care memorează indicele următorului element din listă. Perechea (v[i], next[i]) conține un nod al listei.
Operații cu liste
Inserare
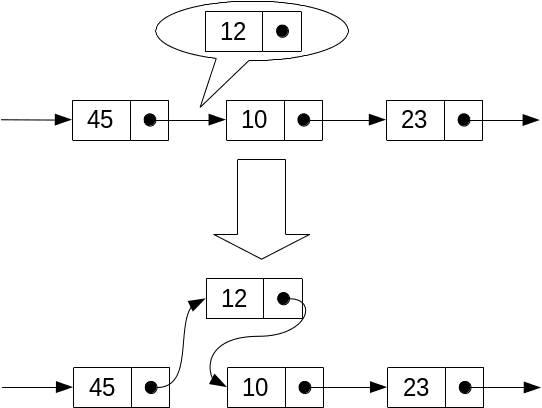 |
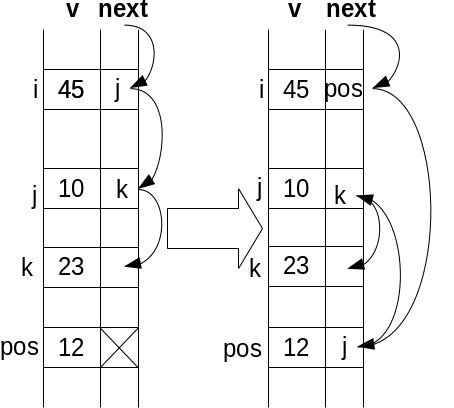 // pos conține poziția nodului de inserat next[pos] = next[i]; next[i] = pos; |
Ștergere
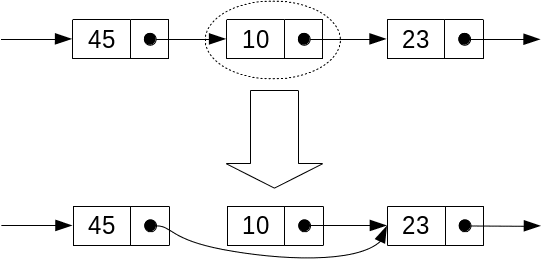 |
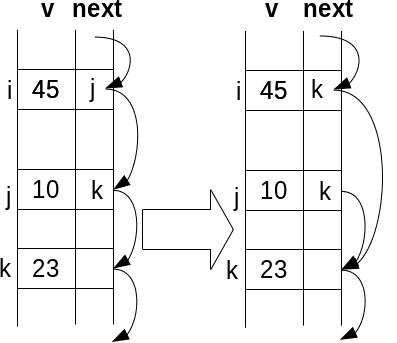 next[i] = next[next[i]]; |
Aplicație 1: v-ați ascunselea
n copii numerotați de la 1 la n și așezați în cerc numără la v-ați ascunselea, din k în k, începînd cu copilul 1. Date n și k să se afișeze ordinea în care ies copiii din cerc.
O rezolvare simplă este să memorăm numerele de la 1 la n într-un vector și apoi să avansăm k elemente și să afișăm elementul curent, iar apoi să îl setăm pe zero. Reluăm căutarea de n ori, ignorînd elementele zero. Deoarece avansul cu k copii poate să dureze n (căci sărim peste elemente zero) soluția are complexitate O(n2):
#include <stdio.h>
int v[100];
int main() {
int n, k, i, j, pos;
scanf( "%d%d", &n, &k );
for ( i = 0; i < n; i++ )
v[i] = i + 1;
pos = n - 1;
for ( i = 0; i < n; i++ ) {
// avanseaza k elemente nenule
for ( j = 0; j < k; j++ ) {
pos = (pos + 1) % n;
while ( v[pos] == 0 )
pos = (pos + 1) % n;
}
printf( "%d ", v[pos] );
v[pos] = 0;
}
printf( "\n" );
return 0;
}
|
O soluție mai eficientă, care folosește liste, are complexitate O(n∙k):
#include <stdio.h>
int v[100], next[100];
int main() {
int n, k, i, j, pos;
scanf( "%d%d", &n, &k );
// initializam lista
for ( i = 0; i < n; i++ ) {
v[i] = i + 1;
next[i] = (i + 1) % n;
}
pos = n - 1; // pos e pozitia copilului din-nainte de copilul de eliminat
for ( i = 0; i < n; i++ ) {
// avanseaza k - 1 elemente deoarece eliminarea conteaza ca un element
for ( j = 1; j < k; j++ )
pos = next[pos];
printf( "%d ", v[next[pos]] );
next[pos] = next[next[pos]];
}
printf( "\n" );
return 0;
}
|
Aplicație 2: bile1
Cei de clasa a 7a ați avut ca temă problema bile1 dată la ONI 2012 clasa a 7a. Problema poate fi rezolvată folosind o matrice caracteristică a obstacolelor. Dar dacă memoria permisă ar fi fost mai mică nu o puteam rezolva în acest fel. Rezolvarea cu liste necesită doar O(m+n+p) memorie. Ca structuri de date vom folosi:
- un vector b[n] care memoreaza linia cu bile, O(n), n fiind numărul de coloane
- un vector liste[m] care pentru linie pointează la o listă de coloane pe care se află obstacole, O(m), unde m este numărul de linii.
- doi vectori paraleli col[p] și next[p] care memoreaza coloanele obstacolelor și următorul obstacol pe linie, O(p), unde p este numărul de obstacole.
Algoritmul folosit este următorul:
1. Citește m, n și p, setează i la zero
2. Citește fiecare obstacol (l, c) si:
2.1 col[i] = c
2.2 adaugă coloana c la lista de pe linia l, liste[l]:
2.2.1 next[i] = liste[l]
2.2.2 liste[l] = i
2.3 i = i + 1
3. Citește vectorul de bile
4. Pentru fiecare linie l de la 1 la m
4.1 parcurge lista de coloane liste[l] si pentru fiecare obstacol col[i] din listă:
4.1.1 actualizează vectorul de bile la indicele coloanei, col[i]
Cum se compară cu algoritmul inițial care folosește o matrice caracteristică? Timpul de execuție este O(m+n+p) față de O(m×n+p). Memoria folosită este O(m+n+p) față de O(m×n). Observăm că atît timpul cît și memoria se îmbunătățesc substanțial.
Vă rămîne ca temă opțională să implementați această soluție.
Aplicație 3: zigzag
Problema zigzag dată la ONI 2012 clasa a 7a are o rezolvare foarte ușoară cu liste. Ca și la bile1, vom ține minte pentru fiecare linie a matricei de codificare cîte o listă cu coloanele unde apar litere. Vom genera aceste liste parcurgînd în matrice pozițiile (l, c) unde s-ar afla textul și adăugînd coloana c la lista liniei l. Apoi vom parcurge aceste liste, în ordine, și vom atașa fiecărei celule, pe lîngă coloană, o literă din text. De fapt vom vedea că nici nu avem nevoie să stocăm coloanele, ci doar literele. În final vom parcurge celulele în ordinea alocării lor, deoarece ea este chiar ordinea textului decodificat.
O diferență față de bile1 este că va trebui să ținem nu numai vectorul cu începutul listelor ci și un vector cu ultimul element din listă pentru a putea face adăugarea la coadă foarte rapid. O alternativă ar fi să parcurgem pozițiile in ordine inversă (pare mai complicat, însă). Să denumim vectorii prim și ultim.
Iată algoritmul de generare a listelor:
// pregatim listele cu pozitiile in matricea cheie
// cheie este cheia, iar n este numărul de caractere al mesajului,
// c aloca celulele listei si este si coloana in acelasi timp
l = 0;
pas = 1; // initial linia creste din unu in unu
// nu putem avea celule pe indexul 0 deoarece cu zero codificam finalul
// de lista, deci codificam coloanele incepind cu 1, no biggie
for ( c = 1; c <= n; c++ ) {
// pentru fiecare coloana a matricei calculam
// linia corespunzatoare literei (este una singura!)
// liniile vor fi de la zero, nici un motiv sa le numerotam de la 1
// avem perechea (l, c): aseaza c in lista l
next[c] = 0; // nu urmeaza nimeni după mine, sint ultima celula
if ( prim[l] == 0 ) // lista este vida
prim[l] = ultim[l] = c;
else // avem un ultim element
ultim[l] = next[ultim[l]] = c;// atasam celula la coada ultimului element
// avanseaza linia
l = l + pas;
if ( l < 0 || l >= cheie ) { // daca am depasit marginea inversam pasul
pas = -pas;
l = l + pas + pas; // adunam de doua ori pasul pentru a ne intoarce
}
}
Vă rămîne ca temă să continuați această implementare. Mai aveți de parcurs listele in ordinea naturală și atașat literele din text, iar la final să parcurgeți celulele în ordinea alocării lor (cu indicele c).
Temă comună pentru ambele clase
- Opțional, ca exercițiu cu liste: bile1 implementată cu liste de obstacole
- oras ca aplicație de flood fill
- zigzag (ONI 2012 clasa 7) rezolvată cu liste. Vă rog foarte mult să nu luați o rezolvare mai veche și să o trimiteți doar pentru a marca tema ca făcută! Scopul este să exersați listele, nu să luați 100p la problemă!
- Opțional, probleme grele, nivel baraj gimnaziu:
Rezolvări aici [2]