Clasa a 7-a Lecția 10: Fill recursiv (flood fill)
Înregistrare video lecție
Despre flood fill
Algoritmul fill umple toate golurile accesibile de la un punct dat.
Golurile pot fi elemente zero într-o matrice, de exemplu, iar vecinii pot fi definiți ca elementele adiacente pe linie și coloană (acesta este cazul cel mai întâlnit). Alteori vecinii pot fi definiți ca având un punct comun cu elementul curent, ceea ce include și elementele alăturate pe diagonală.
Să luăm un exemplu clasic:
Se dă o matrice a[m][n] cu elemente 0 și 1, 0 semnificând liber și 1 semnificând zid, precum și o poziție în matrice, (l, c). Să se spună câte elemente 0 sunt accesibile de la (l, c) avansând doar pe linie sau pe coloană.
int fill( int l, int c ) { // umple de la coloana l, c
int suma = 1; // contorizam punctul curent
a[l][c] = 1; // marcam pozitia ca parcursa
if ( l > 0 && a[l-1][c] == 0 ) // ne deplasam in sus
suma += fill( l - 1, c );
if ( l < m-1 && a[l+1][c] == 0 ) // ne deplasam in jos
suma += fill( l + 1, c );
if ( c > 0 && a[l][c-1] == 0 ) // ne deplasam spre stinga
suma += fill( l, c - 1 );
if ( c < n-1 && a[l][c+1] == 0 ) // ne deplasam spre dreapta
suma += fill( l, c + 1 );
return suma;
}
...
int main() {
int suma;
...
suma = 0;
if ( a[l][c] == 0 )
suma = fill( l, c );
printf( "%d", suma );
...
}
Observații:
- Ordinea direcțiilor nu contează. Cele patru apeluri recursive pot fi în orice ordine.
- Vecinii pot fi în număr de 4 - cei adiacenți pe linie și pe coloană, ca în exemplul de mai sus, sau pot fi în număr de 8 - și cei adiacenți pe diagonale.
Ce complexitate are acest algoritm?
Acest algoritm are complexitate O(m·n) ca timp, deoarece poate parcurge toate elementele matricei, iar prelucrarea per element este O(1). Memoria ocupată este de asemenea O(m·n) deoarece fiecare apel recursiv necesită O(1) memorie și putem avea O(m·n) apeluri recursive unul în altul.
Atenție! Acesta este principalul impediment al metodei! Ea folosește foarte multă memorie suplimentară.
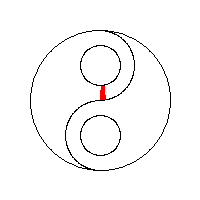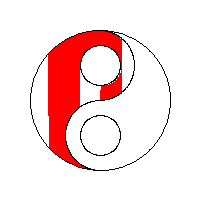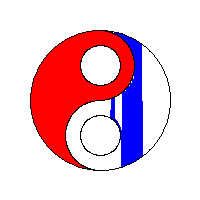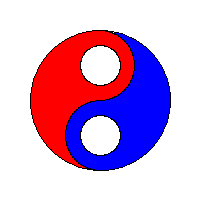
Exemplificare grafică
Să vedem niște vizualizări ale algoritmului flood fill preluate de la wikipedia: algoritm flood fill.
 |
 |
 |
Optimizări ale algoritmului
Bordare matrice
O primă optimizare de timp este clasică. Pentru a face programul atât mai rapid cât și mai scurt putem borda matricea de jur împrejur cu elementul zid, în cazul nostru 1. Astfel vom scuti testul de ieșire a coordonatelor din matrice.
Funcția se simplifică:
int fill( int l, int c ) { // umple de la coloana l, c
int suma = 1; // contorizam punctul curent
a[l][c] = 1; // marcam pozitia ca parcursa
if ( a[l-1][c] == 0 ) // ne deplasam in sus
suma += fill( l - 1, c );
if ( a[l+1][c] == 0 ) // ne deplasam in jos
suma += fill( l + 1, c );
if ( a[l][c-1] == 0 ) // ne deplasam spre stinga
suma += fill( l, c - 1 );
if ( a[l][c+1] == 0 ) // ne deplasam spre dreapta
suma += fill( l, c + 1 );
return suma;
}
Reducere memorie folosită
Cum calculăm memoria ocupată?
Țineți minte: fiecare apel recursiv ocupă memorie echivalentul unui int. Pe un calculator de 32 de biți, cum sunt cele pe care lucrăm noi (ele sunt de fapt de 64 de biți, dar programele sunt compilate în modul 32 de biți), aceasta înseamnă patru octeți.
Aceasta este adresa de întoarcere din funcție. Alte elemente care ocupă memorie pe stivă sunt parametrii transmiși și variabilele declarate în funcție. În cazul nostru vom avea 16 octeți cei doi parametri, variabila declarată în funcție și adresa de întoarcere din funcție.
Dacă micșorarea memoriei folosite este esențială putem elimina 12 octeți din 16, declarând variabilele l, c și suma globale, astfel:
int l, c, suma; // variabile globale
...
void fill() {
suma++;
a[l][c] = 1;
l--;
if ( a[l][c] == 0 ) // apelam pentru (l - 1, c)
fill();
l++;
l++;
if ( a[l][c] == 0 ) // apelam pentru (l + 1, c)
fill();
l--;
c--;
if ( a[l][c] == 0 ) // apelam pentru (l, c - 1)
fill();
c++;
c++;
if ( a[l][c] == 0 ) // apelam pentru (l, c + 1)
fill();
c--; // acum (l, c) sunt cele de la inceput
}
Este o modificare urâtă, care face codul nelizibil, dar uneori necesară la olimpiadă. Nu uitați că chiar și în această formă algoritmul va folosi 4 octeți pe apel recursiv imbricat pentru adresa de revenire din funcție.
Observație: variabilele l și c fiind globale ele trebuie să aibă aceeași valoare la ieșirea din funcție ca și la intrarea în funcție. De aceea ultima instrucțiune c--; este importantă!
Aplicații ce folosesc flood fill și concluzii
Găsire ieșire din labirint
Folosind flood fill putem găsi un punct de ieșire dintr-un labirint memorat într-o matrice. Să presupunem că elementele 0 înseamnă loc gol și cele 1 înseamnă zid. Ieșirile sunt puncte 0 pe marginile matricei. Dat un punct din interiorul matricei, există un drum spre ieșire? Dacă da, putem găsi atât coordonatele ieșirii cât și drumul parcurs.
Iată un exemplu de program care afișează coordonatele ieșirii:
int fill( int l, int c ) {
int retval;
if ( lab[l][c] == BORDER ) // am ajuns la margine?
return l * MAXN + c; // returnam (l, c)
lab[l][c] = 1; // marcam punctul curent ca vizitat
retval = 0; // 0 inseamna ca nu am gasit iesire
if ( lab[l + 1][c] != 1 ) // daca nu este zid
retval = fill(l + 1, c); // cautam in jos
if ( retval == 0 ) { // daca nu am gasit iesire
if ( lab[l - 1][c] != 1 ) // si nu este zid
retval = fill(l - 1, c); // cautam in sus
if ( retval == 0 ) { // daca nu am gasit iesire
if ( lab[l][c + 1] != 1 ) // si nu este zid
retval = fill(l, c + 1); // cautam in dreapta
if ( retval == 0 ) // daca nu am gasit iesire
if ( lab[l][c - 1] != 1 ) // si nu este zid
retval = fill(l, c - 1); // cautam in stinga
}
}
return retval;
}
int main() {
FILE *fin, *fout;
int n, l, c, ls, cs, p;
fin = fopen( "iesire.in", "r" );
fscanf( fin, "%d%d%d ", &n, &ls, &cs );
for ( l = 0; l < n; l++ ) {
for ( c = 0; c < n; c++ ) // citim linia l a matricei
lab[l][c] = fgetc( fin ) - '0';
fgetc( fin ); // citim '\n'
}
fclose( fin );
for ( c = 0; c < n; c++ ) { // bordare conditionala margini
if ( lab[0][c] == 0 )
lab[0][c] = BORDER;
if ( lab[n - 1][c] == 0 )
lab[n - 1][c] = BORDER;
if ( lab[c][0] == 0 )
lab[c][0] = BORDER;
if ( lab[c][n - 1] == 0 )
lab[c][n - 1] = BORDER;
}
p = fill( ls - 1, cs - 1 );
fout = fopen( "iesire.out", "w" );
if ( p > 0 )
fprintf( fout, "%d %d\n", 1 + p / MAXN, 1 + p % MAXN );
else
fprintf( fout, "-1\n" );
fclose( fout );
return 0;
}
Arie goluri
Calcul arie goluri: dorim să aflăm numărul de elemente zero accesibile din punctul inițial.
Iată un exemplu de program care afișează aria golului accesibil din punctul inițial:
#include <stdio.h>
#define MAXN 1000
#define BORDER 2
char lab[MAXN + 2][MAXN + 2]; // matricea labirint
// Executa flood fill de la coordonate (l, c)
// returneaza aria zonei din care se porneste fill (cite puncte 0)
int fill( int l, int c ) {
int aria;
lab[l][c] = 1; // marcam punctul curent ca vizitat
aria = 1; // contorizam punctul curent
if ( lab[l + 1][c] == 0 ) // daca nu este zid
aria += fill(l + 1, c); // cautam in jos
if ( lab[l - 1][c] == 0 ) // daca nu este zid
aria += fill(l - 1, c); // cautam in sus
if ( lab[l][c + 1] == 0 ) // daca nu este zid
aria += fill(l, c + 1); // cautam in dreapta
if ( lab[l][c - 1] == 0 ) // daca nu este zid
aria += fill(l, c - 1); // cautam in stinga
return aria;
}
int main() {
FILE *fin, *fout;
int n, l, c, ls, cs, a;
fin = fopen( "arie.in", "r" );
fscanf( fin, "%d%d%d ", &n, &ls, &cs );
for ( l = 1; l <= n; l++ ) {
for ( c = 1; c <= n; c++ ) // citim linia l a matricei
lab[l][c] = fgetc( fin ) - '0';
fgetc( fin ); // citim '\n'
}
fclose( fin );
for ( c = 1; c <= n; c++ ) // bordare margini
lab[0][c] = lab[n + 1][c] = lab[c][0] = lab[c][n + 1] = BORDER;
a = fill( ls, cs ); // calcul arie accesibila din (ls, cs)
fout = fopen( "arie.out", "w" );
fprintf( fout, "%d\n", a );
fclose( fout );
return 0;
}
Număr goluri
Calcul număr de goluri: denumite și componente conexe, putem folosi fill pentru a număra câte goluri disjuncte există (astfel încât să nu se poată ajunge de la un gol la altul). Pentru aceasta vom parcurge matricea în orice ordine și vom porni câte un fill din fiecare loc unde găsim un element 0.
Iată un exemplu de program:
#include <stdio.h>
#define MAXN 1000
#define BORDER 2
char lab[MAXN + 2][MAXN + 2]; // matricea labirint
// Executa flood fill de la coordonate (l, c)
void fill( int l, int c ) {
lab[l][c] = 1; // marcam punctul curent ca vizitat
if ( lab[l + 1][c] == 0 ) // daca nu este zid
fill(l + 1, c); // cautam in jos
if ( lab[l - 1][c] == 0 ) // daca nu este zid
fill(l - 1, c); // cautam in sus
if ( lab[l][c + 1] == 0 ) // daca nu este zid
fill(l, c + 1); // cautam in dreapta
if ( lab[l][c - 1] == 0 ) // daca nu este zid
fill(l, c - 1); // cautam in stinga
}
int main() {
FILE *fin, *fout;
int n, l, c, ls, cs, nr;
fin = fopen( "nrgol.in", "r" );
fscanf( fin, "%d%d%d ", &n, &ls, &cs );
for ( l = 1; l <= n; l++ ) {
for ( c = 1; c <= n; c++ ) // citim linia l a matricei
lab[l][c] = fgetc( fin ) - '0';
fgetc( fin ); // citim '\n'
}
fclose( fin );
for ( c = 1; c <= n; c++ ) // bordare margini
lab[0][c] = lab[n + 1][c] = lab[c][0] = lab[c][n + 1] = BORDER;
nr = 0;
for ( l = 1; l <= n; l++ )
for ( c = 1; c <= n; c++ ) // pentru fiecare punct din labirint
if ( lab[l][c] == 0 ) { // daca nu este zid si nu a fost umplut deja
nr++; // contorizam un nou gol
fill( l, c ); // umplem zona
}
fout = fopen( "nrgol.out", "w" );
fprintf( fout, "%d\n", nr );
fclose( fout );
return 0;
}
Perimetru goluri
Calcul perimetru goluri: în locul ariei golurilor putem calcula perimetrul lor, anume numărul de puncte din goluri care se învecinează cu un punct care nu face parte din gol. Trebuie să avem grijă când testăm dacă un punct este pe perimetru.
Un punct se află pe perimetru dacă:
- Unul din vecinii săi este zid,
- Sau unul din vecinii săi este margine bordată.
Un punct nu neapărat se află pe perimetru dacă:
- Unul din vecinii săi este un alt punct parcurs anterior.
Cum ne dăm seama dacă vecinul este margine, zid, sau punct anterior?
Vom umple golurile cu un număr distinct. În exemplul de mai jos marginile și zidurile sunt codificate cu 1, iar umplerea se face cu 2.
Iată un exemplu de program care afișează perimetrul golului accesibil din punctul inițial:
#include <stdio.h>
#define MAXN 1000
#define BORDER 1
#define FILL 2
char lab[MAXN + 2][MAXN + 2]; // matricea labirint
// Executa flood fill de la coordonate (l, c)
// returneaza perimetrul zonei din care se porneste fill (cite puncte 0)
int fill( int l, int c ) {
int perimetrul;
lab[l][c] = FILL; // marcam punctul curent ca vizitat
perimetrul = lab[l - 1][c] == 1 // verificam daca punctul curent este pe
|| lab[l + 1][c] == 1 // perimetru
|| lab[l][c - 1] == 1
|| lab[l][c + 1] == 1; // daca da, contorizam punctul curent
if ( lab[l + 1][c] == 0 ) // daca nu este zid
perimetrul += fill(l + 1, c); // cautam in jos
if ( lab[l - 1][c] == 0 ) // daca nu este zid
perimetrul += fill(l - 1, c); // cautam in sus
if ( lab[l][c + 1] == 0 ) // daca nu este zid
perimetrul += fill(l, c + 1); // cautam in dreapta
if ( lab[l][c - 1] == 0 ) // daca nu este zid
perimetrul += fill(l, c - 1); // cautam in stinga
return perimetrul;
}
int main() {
FILE *fin, *fout;
int n, l, c, ls, cs, p;
fin = fopen( "perimetru.in", "r" );
fscanf( fin, "%d%d%d ", &n, &ls, &cs );
for ( l = 1; l <= n; l++ ) {
for ( c = 1; c <= n; c++ ) // citim linia l a matricei
lab[l][c] = fgetc( fin ) - '0';
fgetc( fin ); // citim '\n'
}
fclose( fin );
for ( c = 0; c < n; c++ ) // bordare margini
lab[0][c] = lab[n + 1][c] = lab[c][0] = lab[c][n + 1] = BORDER;
p = fill( ls, cs ); // calcul perimetru accesibil din (ls, cs)
fout = fopen( "perimetru.out", "w" );
fprintf( fout, "%d\n", p );
fclose( fout );
return 0;
}
Eliminare zid
Ne propunem să eliminăm acea pătrațică zid care reduce la minim numărul de goluri.
Cum procedăm?
Soluție forță brută: o soluție forță brută ar fi să eliminăm pe rând fiecare bucată de zid și să numărăm golurile formate.
Ce complexitate are această soluție?
Deoarece numărul de ziduri poate fi O(n2) iar numărarea golurilor este și ea tot O(n2) rezultă o complexitate de O(n4).
Se poate mai bine? Desigur.
Soluție optim: soluția optimă este similară cu cea care numără golurile:
- Umplem toate golurile.
- La fiecare gol umplem cu o valoare diferită de fill.
- La final parcurgem matricea căutând pătrățica zid care are ca vecini cele mai multe goluri diferite (eticheta diferită).
Ce complexitate are această soluție?
- Umplerea golurilor este O(n2).
- Verificarea zidurilor este O(n2).
Timpul total va fi, deci, O(n2).
Concluzii
Fill este o unealtă simplă și utilă, ușor de folosit la concursuri. Principalul ei neajuns este memoria ocupată.
Ce facem în situația când matricea este prea mare și memoria disponibilă insuficientă pentru a folosi flood fill?
În această situație putem folosi BFS fill (breadth first search), care, atunci când este aplicat pe o matrice se mai numește și algoritmul Lee. El folosește o coadă pentru a menține frontiera deja acoperită, reducând memoria la O(m+n) însă fiind ceva mai lent.
Vom discuta acest algoritm într-o altă lecție.
Temă 10
Să se rezolve următoarele probleme (program C trimis la NerdArena):
Temă opțională
Să se rezolve următoarele probleme (program C trimis la NerdArena):
- OZN dată la barajul pentru Shumen din Tudor Vianu anul 2014, juniori