Clasa a 7-a Lecția 19: Cozi și algoritmul lui Lee

Înregistrare video lecție

Tipul coadă

Coada (în engleză queue) este o grămadă de obiecte ordonate după ordinea FIFO: first in, first out. Aceasta înseamnă că putem adăuga obiecte în coadă, iar atunci când le vom scoate, le vom scoate în aceeași ordine în care le-am adăugat. Ne aducem aminte că, prin contrast, stiva scoate obiectele în ordine inversă față de cum au fost adăugate (ordine LIFO).

Coada ca tip de date abstract

Ne aducem aminte despre ideea de tip de date abstract: un tip de date abstract este un model matematic. Acest model definește operații asupra tipului de date, precum și restricții asupra efectului acestor operații. Tipurile de date abstracte sunt utile în simplificarea algoritmilor, deoarece descompun problema în subprobleme mai mici, cunoscute și studiate.

Tipul de date abstract coadă definește operațiile:

enqueue, care adaugă un element la coadă
dequeue, care scoate un element din coadă
empty, care ne spune dacă coada este goală
full, care ne spune dacă coada este plină

Restricțiile sunt asupra ordinii de returnare a elementelor și anume ele trebuie returnate după regula primul venit primul plecat. De aceea se spune că o coadă este o structură de tip FIFO (first in, first out).

Implementarea cozilor cu vectori circulari

Precum am mai spus, tipurile de date abstracte separă funcționalitatea de implementare. În cazul cozii există mai multe implementări posibile. Noi vom studia una dintre cele mai folosite: implementarea cu vectori circulari. Această implementare:

Folosește un vector pentru a păstra elementele și doi indici, primul și ultimul care memorează poziția primului, respectiv ultimului element din coadă. Pentru a nu deplasa elemente atunci când scoatem un element din coadă vom incrementa doar poziția primului element. Atunci când adăugăm un element în coadă incrementăm poziția ultimului element.
Pentru a refolosi golurile rămase în urmă la scoaterea din coadă și a nu deplasa cei doi indici la infinit vom defini o mărime maximă a cozii, n. Atunci când unul din indici depășește această mărime el revine la zero. Logic vorbind după ultimul element din vector urmează din nou primul. De aceea spunem că vectorul este circular. Formula de actualizare a indicilor devine primul = (primul + 1) % n și ultimul = (ultimul + 1) % n, unde n este numărul maxim de elemente din coadă.

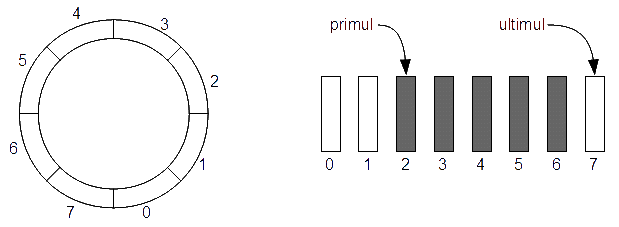
Observăm că primul este poziția primului element din coadă, iar ultimul este poziția primului element liber din vector.
Coadă goală. Cum răspundem la întrebarea este coada goală? Se observă că acest lucru se întâmplă când primul == ultimul.
Coada plină. Cum răspundem la întrebarea este coada plină? Observăm că aceasta se întâmplă tot atunci când primul == ultimul. Pentru a diferenția între aceste două cazuri vom sacrifica un element din vector, folosind numai n-1 poziții. În felul acesta testul de coadă plină va fi (ultimul + 1) % n == primul.

Observații:

În această implementare cele patru operații au complexitate O(1).
Important: în practică, pentru a nu face împărțiri, dimensiunea maximă a cozii va fi o putere a lui doi, constantă definită în program.
Unul din avantajele acestei implementări, de care veți auzi în detaliu în facultate este că scoaterea de elemente se poate face în paralel cu adăugarea, de exemplu în cazul când un proces generează elementele de adăugat și un alt proces, independent, colectează elementele spre procesare.

Exemple de probleme ce folosesc tipul coadă

Exemple de probleme ce folosesc cozi în rezolvări:

Maxim dată la concursul ONI 2019 clasa a 6-a (punctul 2)
Livada dată la cercul de informatică Vianu 2014 clasa a 9-a

La pbinfo.ro:

Algoritmul lui Lee (BFS Fill)

În anul 1961 C. Y. Lee a publicat un algoritm de studiu al căilor de conectare între două puncte în diagrame electronice. Algoritmul original presupune o rețea plană (un circuit electronic) în care, mulțumită proprietăților curentului electric, toate muchiile sunt de lungime unu. De-a lungul timpului (și aparent mai mult în România) acest algoritm a ajuns să fie asociat cu parcurgerea pe lățime a unei matrice, drept pentru care acesta este modul în care îl voi prezenta aici.

Deoarece algoritmul lui Lee este o parcurgere pe lățime ar trebui predat după conceptul de parcurgere pe lățime. De aceea, în această lecţie, voi încerca să prezint ambele.

Aplicații ale parcurgerii pe lățime

Găsirea drumului minim de la un punct la un altul, sau la mai multe puncte finale.
Mai puțin menționat: fill cu mai puțină memorie suplimentară (dar și mai lent)

Pentru exemplificare, să considerăm următoarea problemă: se dă un labirint codificat ca o matrice cu zero și unu, zero semnificând loc liber și unu fiind element obstacol (zid). Se dau de asemenea un punct de start și unul de final. În matrice ne putem deplasa pe linie sau pe coloană, cu condiția să nu avem un obstacol. Să se calculeze, lungimea drumului minim între cele două puncte, dacă există un astfel de drum.

Parcurgerea în adîncime

Când am discutat despre algoritmul flood fill am menționat că el este o parcurgere a matricei în adâncime, deoarece traversarea elementelor matricei se face avansând din vecin în vecin până ce se ajunge la o fundătură (un obstacol, ieșire din matrice, sau element deja parcurs). Am denumit această parcurgere DFS (depth first search), aceasta însemnând că în alegerea noului element de vizitat preferăm adâncimea. Ne putem imagina această parcurgere cu un fir subțire de apă care curge într-o direcție oarecare, apoi, când nu mai poate schimbă direcția. Când ramura curentă se "înfundă" apa se va ramifica din firul principal undeva cel mai aproape de fundătură, acolo unde o poate lua pe altă direcție.

Am menționat atunci că pentru acest tip de parcurgere avem nevoie de o stivă pentru memorarea elementelor ce urmează a fi parcurse. Stiva este fie explicită (nu am vorbit despre aceasta), fie implicită, într-o implementare recursivă. Această stivă are consecințe: ea adaugă O(M x N) memorie suplimentară.

Folosind parcurgerea în adâncime, flood fill, putem răspunde la întrebarea dacă există drum între cele două puncte, dar nu putem calcula drumul minim.

Parcurgerea pe lățime

Prin contrast, ne putem imagina o parcurgere pe lățime. În această parcurgere vom traversa mai întâi elementele vecine cu elementul de start. Apoi vom continua cu elementele vecine cu ele. Și apoi cu elementele vecine cu vecinele, și așa mai departe. Putem vizualiza această parcurgere dacă ne imaginăm că turnăm apă în punctul de pornire. Ea se va împrăștia uniform în toate direcțiile. Dacă va da de obstacole ea va merge de-a lungul lor și le va ocoli. La orice moment distanța între orice punct de pe frontiera apei și punctul de start este aceeași.

Denumim această parcurgere BFS (breadth first search), deoarece în alegerea noului element de parcurs vom prefera lățimea. La fiecare iterație k vom trata elementele aflate la distanță k de punctul original. Ele formează frontiera (marginea) apei, în exemplul nostru. După fiecare iterație frontiera va fi înlocuită cu o nouă frontieră aflată la distanță mai mare cu unu decât vechea frontieră.

Precum vom vedea mai jos această parcurgere este similară cu cea în adâncime, diferența fiind că ea folosește o coadă în loc de stivă pentru memorarea elementelor ce urmează a fi parcurse. Spre deosebire de flood fill, coada trebuie să fie explicită. De aceea algoritmul poate părea foarte diferit de flood fill, dar, în realitate nu este.

Exemplificare grafică

Să vedem niște vizualizări ale algoritmului BFS fill preluate de la wikipedia: algoritm flood fill:

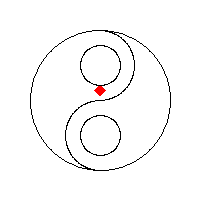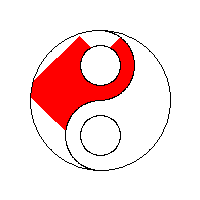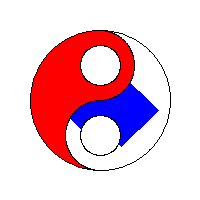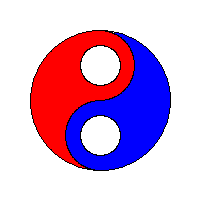
Implementarea parcurgerii pe lățime în matrice

Cum implementăm parcurgerea pe lățime? Cum memorăm frontiera? O idee imediată ar fi să ținem două frontiere: cea curentă, în curs de procesare, și cea nouă, în curs de generare. La fiecare iterație calculăm o nouă frontieră pe baza celei dinainte. Apoi comutăm pe frontiera cea nouă. Ce conțin frontierele (ce stocăm)? Vom păstra identificatorii unici ai elementelor matricei, respectiv linia și coloana. Frontierele vor fi vectori de perechi (linie, coloană). Această metodă funcționează, dar nu este nici cea mai simplă și nici cea mai economică ca memorie.

În practică nu vom face distincția între frontiera veche și cea nouă. Elementele din frontiera nouă vor fi adăugate la frontiera veche, la sfârșit. Vom avea astfel o singură frontieră de elemente de procesat. Vom procesa elementele de la începutul frontierei și vom adăuga elementele noi, vecinii, la finalul frontierei. În imaginea noastră cu apa punctele procesate vor descrie o spirală în jurul punctului de pornire.

În acest fel ajungem la structura de date pe care o vom folosi pentru stocarea punctelor de frontieră: coada. Așa cum am menționat mai sus, în loc de stivă vom folosi o coadă de perechi (linie, coloană) pentru stocarea elementelor ce urmează a fi parcurse. La un pas vom extrage din coadă primul element și vom adăuga elementele vecine lui la finalul cozii, câtă vreme ele nu se află deja în coadă (coada conține numai elemente unice).

Algoritmul de parcurgere BFS

Iată o schiță de algoritm, care nu este neapărat universal valabil, dar poate fi adaptat diverselor situații. Această versiune de algoritm își propune să găsească cel mai scurt drum de la (lstart, cstart) la (lend, cend):

Inițializează matricea labirint L[][] cu 0 pentru loc liber și -1 pentru obstacol Inițializează coada cu elementul de pornire (lstart, cstart) Setează L[lstart][cstart] // distanța inițială Execută: Scoate primul element din coadă. Fie el linia (lin, col) Setează dist // distanța acestui element Pentru fiecare vecin (l, c) al lui (lin, col) Dacă L[l][c] = 0 // nu se află în coadă și nici nu este obstacol Adaugă (l, c) în coadă Setează L[l][c] Câtă vreme coada nu este vidă și (lin, col) nu este destinația (lend, cend) Afișează L[lin][col] // distanța până la cel mai apropiat punct destinație

Note de implementare

Vecinii unui element din matrice pot fi fie cei adiacenți pe linie și coloană, fie și cei pe diagonală, algoritmul funcționează la fel.
De obicei vom folosi tehnicile învățate:
- Bordarea matricelor pentru a scăpa de testul de ieșire din matrice
- Vectorii de direcție pentru a genera ușor vecinii
Problema poate fi considerată una de simulare: simulăm parcurgerea tuturor traseelor optime în același timp.
Dacă nu există drum între cele două puncte algoritmul se va termina când coada devine goală.
În funcție de ceea ce se cere (drum minim până la destinație, drum minim până la anumite puncte, sau drum minim până la toate elementele matricei) coada poate fi parcursă până la final, sau ne putem opri când anumite condiții ale simulării au fost îndeplinite, cum ar fi atingerea punctului destinație.
Cum știm dacă un element se află deja în coadă? Printr-o matrice de frecvență: la momentul adăugării în coadă vom marca aceasta în matrice. De cele mai multe ori putem combina matricea de frecvență cu matricea de distanțe (ca în algoritmul de mai sus): un element diferit de zero semnifică distanța acelui element la punctul de start. În această notație obstacolele trebuie memorate ca numere negative pentru a nu fi confundate cu distanțe.
Cum știm că am ajuns în punctul final? Putem să testăm explicit linia și coloana. Dar dacă avem mai multe puncte finale trebuie să le marcăm într-o matrice. Această matrice se poate de obicei combina cu matricea de frecvență și cu cea de distanțe, deoarece avem nevoie doar de un bit unu sau zero.
Algoritmul poate fi adaptat să calculeze drumul minim de la mai multe puncte de pornire la mai multe puncte destinație. În acest caz vom inițializa coada cu toate punctele de pornire.

Reconstrucția drumului minim

Pentru a reconstitui un drum minim între sursă și destinație vom porni invers: de la destinație și vom avansa în L[][] pe elemente descrescătoare din unu în unu, până ce ajungem la sursă. Atenție, drumul nu este neapărat unic.

Implementarea cozii de coordonate

Pentru coadă vom folosi un vector circular de mărime 2(M+N) (vezi explicația la capitolul de complexități). Vom avea o variabilă, prim care păstrează indicele de adăugare în coadă, precum și o variabilă ultim care păstrează poziția primului element gol, în afara cozii. Acești doi indici vor avansa circular, modulo mărimea cozii.

Coada poate să fie un vector de elemente tip struct, sau doi vectori separați. Prima variantă este mai bună din punct de vedere cache, dar poate duce la risipă de memorie în anumite situații, dacă elementul de tip struct nu ocupă un număr de octeți divizibil cu patru (sau cu lungimea cuvântului de memorie).

Vom folosi trei funcții:

enqueue( lin, col ) care adaugă elementul (lin, col) în coadă.
dequeue() care extrage elementul (lin, col) din coadă.
emptyqueue() care returnează 1 dacă coada este vidă.

Iată o posibilă implementare ce presupune că numărul de linii și coloane este maxim 255:

int prim, ultim;
unsigned char coadal[NCOADA], coadac[NCOADA]; // coordonate mici

// adauga coordonate in coada
static inline void enqueue( int l, int c ) {
  coadal[ultim] = l;
  coadac[ultim] = c;
  ultim = (ultim + 1) % NCOADA;
}

// scoate coordonate din coada
static inline int dequeue() {
  int retval = coadal[prim] * 256 + coadac[prim];

  prim = (prim + 1) % NCOADA;

  return retval;
}

// returneaza 1 cand coada este goala
static inline int emptyqueue() {
  return prim == ultim;
}

Observații:

Funcția dequeue() returnează două valori, linie și coloană. Ele fiind mici le-am combinat într-un singur întreg. Acest lucru este posibil în general, deoarece putem combina două valori unsigned short într-un unsigned int, ceea ce ne permite linii și coloane până în 65535, număr în general acoperitor pentru o matrice stocată în memorie.
Astfel am putea să stocăm în coadă direct produsul returnat de funcția dequeue(). Avantajele se datorează, în mare, cache-ului.

Complexități în timp și spațiu

Timpul de execuție este O(M x N) deoarece fiecare element al matricei va fi luat în calcul cel mult o dată.

Memoria necesară este O(M x N) deoarece avem nevoie de matricea de distanțe, matricea de frecvențe și cea de puncte terminale, precum și memoria ocupată de coadă. În realitate, de cele mai multe ori putem unifica matricele suplimentare, unindu-le cu matricea labirint. În acest caz memoria suplimentară este cea a cozii. La momentul când scriu aceste rânduri nu am găsit o estimare asupra dimensiunii maxime a cozii necesare. Intuitiv ea este O(M + N), deoarece frontiera, într-un labirint fără obstacole, când punctul de pornire este în mijloc, nu va depăși M+N. Este neclar dacă o altă matrice și un alt punct de pornire o poate face să depășească M + N și cu cât. Ca practică de implementare sfatul meu este să o dimensionați de 2(M + N), acoperitor, deoarece este un număr oricum mult mai mic decât matricea deja stocată, M x N.

Datorită consumului atât de mic de memorie suplimentară, algoritmul lui Lee poate fi folosit ca și ca algoritm de fill pe matrice mari, sau când memoria suplimentară este mică. El va fi însă mai lent decât flood fill, de obicei de multe ori (20-30 de ori), ceea ce dovedește încă o dată că, pentru unii algoritmi, memoria suplimentară se traduce în timp de execuție mai mic.

Aplicații

Algoritmul lui Lee este necesar când dorim să aflăm informații despre drumuri și distanțe:

Găsirea ieșirii dintr-un labirint / castel / hartă.
Găsirea celui mai scurt drum între două puncte dintr-o matrice.
În lumea reală, proiectarea de circuite electronice.

Exemple de probleme ce folosesc algoritmul lui Lee

Orice problemă rezolvabilă prin flood fill este, desigur, rezolvabilă și cu Lee, folosind mai puțină memorie, dar consumând mai mult timp pentru executarea programului. N-am găsit foarte multe exemple de probleme ce necesită Lee, dar nu se pot rezolva cu flood fill. Iată câteva exemple:

Exemple de probleme ce folosesc algoritmul lui Lee în rezolvări:

La NerdArena:

Alee dată la OJI 2007 clasa a 10-a
Insule dată la OJI 2009 clasa a 10-a
Miting dată la OJI 2016 clasa a 10-a (grea)

La InfoArena:

Articolul de la Infoarena include câteva exemple
Muzeu
Traseu3 dată la ONI 2014, clasa a 9-a (Lee 3D, relativ ușoară)
Gheizere dată la ONI 2012, clasa a 10-a (problemă grea)
AI dată la OJI 2011, clasa a 10-a (enunț complex)

Tema 19

Să se rezolve următoarele probleme (program C trimis la NerdArena):

Livada
Alee alee dată la OJI 2007 clasa a 10-a

Tema opțională