Clasa a 7-a Lecția 21: Cozi duble și maximul în fereastră glisantă

Tipul deque (coadă dublă)

Coada dublă este o coadă la care putem adăuga și scoate din ambele capete. Poate fi considerată ca o coadă și o stivă într-o singură structură de date, cu diferența că în coada dublă putem adăuga la începutul cozii.

Cum implementăm o coadă dublă?

O putem implementa la fel ca pe o coadă, într-un vector circular și folosind doi indici, primul și ultimul.

• Adăugarea unui element la final de coadă dublă, precum și eliminarea unui element de la început de coadă dublă se face întocmai ca la o coadă obișnuită.
• Eliminarea unui element de la final se face astfel:

int pop() {
  ultim = (ultim - 1 + QMAX) % QMAX;
  return coada[ultim];
}

• Adăugarea unui element la început se face astfel:

void pushFront( int e ) {
  prim = (prim - 1 + QMAX) % QMAX;
  coada[prim] = e;
}

Vom vedea că operațiunile pe biți pot simplifica puțin modificarea indicilor primul și ultim.

Observație: toate operațiunile pe o coadă dublă se fac în timp constant, O(1).

Maximum în fereastră glisantă (maximum over a sliding window)

• Enunț: dându-se un șir de n numere considerăm cele n – k + 1 subsecvențe de k numere consecutive în șir (denumite și ferestre de lungime k). Putem vedea aceste ferestre ca pe o singură fereastră, deplasabilă, care ne dă acces la k elemente din vector odată. Se cere ca pentru fiecare fereastră să se găsească maximul.
• Algoritmul de rezolvare trivial (forță brută) recalculează maximul pentru fiecare din ferestre, având complexitate O(kn).
• Pentru a reduce complexitatea găsirii maximului procedăm astfel: luăm prima fereastră, de la 0 la k-1. Să spunem că maximul se află pe poziția p₁. Pe măsură ce vom deplasa fereastra este imposibil ca elementele dinaintea maximului să fie vreodată maximul ferestrei, deoarece ele vor face parte împreună cu maximul din această fereastră. Să considerăm poziția celui mai mare element după maxim și la dreapta lui, în fereastră. Fie ea p₂. Rezultă că nici un element pe pozițiile intermediare i, p₁ 2, nu poate fi vreodată maxim în fereastră, deoarece aceste elemente vor fi împreună cu p₂ în toate ferestrele care le conțin. Similar, considerând p₃ poziția următorului maxim, nici un element între p₂ și p₃ nu va putea fi maxim.

În figură noul maxim va elimina din coadă maximele 2 și 3. Coada rămasă va conține maximul 1 și maximul nou

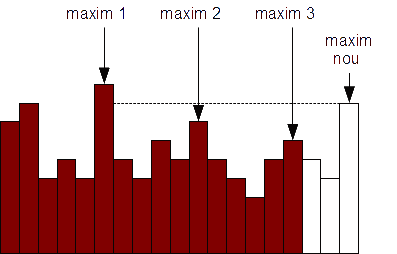
În urma acestor observații apare următorul algoritm:

• Memorăm toate maximele descrescătoare din prima fereastră, într-o coadă dublă. Primul element din coadă este maximul ferestrei.
• Când deplasăm fereastra trebuie să actualizăm structura de maxime din coadă. Pentru aceasta dăm atenție elementului care dispare din fereastră și celui care intră în fereastră.
• Dacă elementul care iese nu este maximul curent, nu avem nimic de făcut.
• Dacă este maximul curent vom scoate primul element din coada de maxime.
• Dacă elementul proaspăt adăugat în fereastră este mai mic decât ultimul maxim din coadă se adaugă la coadă. În caz contrar el va arunca ultimul element, iar și încercăm din nou adăugarea în coadă.
• Rezultă că noul element din fereastră aruncă toate elementele de la urma cozii strict mai mici ca el, iar apoi îl adăugăm normal la coadă.

Observații

• Atunci când eliminăm de la începutul cozii maximul care iese din fereastra glisantă coada dublă acționează ca o coadă.
• Atunci când eliminăm din coadă toate elementele de la final care sunt mai mici decât elementul ce intră în fereastra glisantă, coada dublă acționează ca o stivă.
• Atunci când adăugăm la final elementul care intră în fereastra glisantă coada dublă acționează atât ca o stivă cât și ca o coadă.

Exemplu de cod

Iată un exemplu de implementare. În programul următor:

• n este numărul de elemente citit la intrare.
• k este mărimea ferestrei glisante.
• deq[] este coada dublă ce memorează k elemente, dar va fi dimensionată la următoarea putere a lui 2.
• rasp[] este vectorul de răspunsuri, dar care este folosit și la stocarea elementelor de la intrare, pentru a ști ce iese din fereastră; rasp[] este maximul din fereastra ce începe la poziția i.

  fin = fopen( "mfg.in", "r" );
  fscanf( fin, "%d%d", &n, &k );
  for ( i = 0; i < n; i++ ) {
    if ( i >= k ) {
      if ( (max = deq[prim]) == rasp[i - k] ) // daca max iese din fereastra
        prim = (prim + 1) % MAXK_P2;          // elimina maximul din fereastra
      // stocheaza raspunsul pentru fereastra [i-k..i-1]
      // este ok sa suprascriem rasp[i - k], el nu va mai fi necesar
      rasp[i - k] = max; 
    }
    
    rasp[i] = h = readInt(); // stocam inaltimea curenta, e nevoie la iesire
    while ( ultim != prim && deq[ultim - 1] < h ) // elimina din coada
      ultim = (ultim - 1 + MAXK_P2) % MAXK_P2;    // cata vreme h e mai mare
    deq[ultim] = h;          // depunem inaltimea curenta in coada
    ultim = (ultim + 1) % MAXK_P2;
  }
  fclose( fin );
  rasp[n - k] = deq[prim];   // stocam separat ultimul maxim - caz particular

Complexitate

• La prima vedere pare că, la fiecare pas, putem elimina k elemente din coada dublă, deci complexitatea ar părea O(kn).
• Folosind analiza amortizată rezultă complexitatea reală ca fiind O(n). Fiecare element este adăugat în coadă o dată și este scos cel mult o dată.
• Memoria suplimentară folosită este mărimea maximă a cozii, adică O(k).

Aplicație: numărul maxim ce se poate forma prin eliminarea a K cifre

Enunț: dat un număr de N cifre, dorim să eliminăm K cifre. Să se afișeze numărul maxim ce se poate forma astfel.

Cum rezolvăm această problemă și ce legătură are ea cu maximul în fereastră glisantă?

La prima vedere problema pare complicată. Numărul este foarte mare. Și atunci încercăm să o simplificăm:

• Putem afla care este prima cifră a acestui număr?
• Știm că numărul va avea N-K cifre.
• Este clar că numărul va începe cu una din primele K+1 cifre. De ce? Deoarece dacă el începe cu a K+2-a cifră, ar trebui să eliminăm K+1 cifre de la începutul numărului, ceea ce nu putem.
• Vrem ca prima lui cifră să fie cât mai mare.
• Este, deci, logic, că prima cifră a numărului va fi maximul din primele K+1 cifre. Să presupunem că cifra maximă este a cincea.
• Pentru ca a cincea cifră să devină prima trebuie să eliminăm primele patru cifre.
• Am rămas deci cu restul numărului, ce are N-5 cifre (patru eliminate, una selectată), din care mai avem de eliminat K-4 cifre.
• Putem deci relua metoda, cu un număr mai mic.

Ce facem dacă în primele K+1 cifre avem mai multe maxime dintre care să alegem? Vom alege primul maxim, deoarece nu vrem să eliminăm cifre maximale.

Rezultă următorul algoritm:

Algoritmul 1

1. Citește de la intrare primele K cifre.
2. Câtă vreme mai avem cifre de eliminat (K > 0)
   1. Citește încă o cifră de la intrare.
   2. Calculează maximul dintre primele K+1 cifre. Fie cifra C pe poziția P.
   3. Afișează la ieșire cifra C.
   4. Elimină din cifrele memorate primele P-1 cifre.
   5. K = K - (P - 1)
3. Citește cifrele rămase la intrare și afișează-le.

Observații:

• Algoritmul selectează, pe rând, cifrele rămase, în loc să se concentreze pe cifrele eliminate.
• Algoritmul nu specifică cum găsim maximul cifrelor. O căutare liniară ar duce la un algoritm ineficient.

Cum găsim eficient maximul din primele K+1 cifre? Folosind o coadă dublă. Vom avea o fereastră glisantă de lungime variabilă. Ea va avea la început lungimea K+1, iar apoi va scădea pe măsură ce scade K.

Rezultă algoritmul:

Algoritmul 2

1. Depune primele K cifre de la intrare într-o coadă dublă, păstrând doar maxime consecutive descrescătoare, dar memorând și pozițiile lor.
2. Câtă vreme mai avem cifre de eliminat (K > 0)
   1. Citește încă o cifră de la intrare și depune-o în coadă cu poziția sa, eliminând cifrele mai mici ca ea.
   2. Prima pereche din coadă va fi maximul C, cu poziția sa P.
   3. Afișează la ieșire cifra C.
   4. Elimină prima pereche din coadă.
   5. K = K - (P - 1)
3. Citește cifrele rămase la intrare și afișează-le

Observații:

• Algoritmul se poate aplica și pentru numărul minim, cu o singură diferență: nu putem alege ca primă cifră minimă o cifră zero. Următoarele cifre pot fi zero.
• În realitate, dacă urmărim acest algoritm cu atenție, coada va conține întotdeauna maximele celor K+1 elemente din care dorim să găsim maximul. Explicație: cifrele eliminate sunt eliminate și din coadă. Singura cifră care dispare din coadă este cea afișată, pe care o compensăm la pasul 2.1 citind încă o cifră.

Astfel, algoritmul de mai sus se simplifică, nemaiavând nevoie să stocăm indici, ci doar valori. Să vedem.

Algoritmul 3

1. Depune primele K cifre de la intrare într-o coadă dublă, păstrând doar maxime consecutive descrescătoare.
2. Câtă vreme mai avem cifre de citit
   1. Citește încă o cifră de la intrare și depune-o în coadă, eliminând cifrele mai mici ca ea.
   2. Prima cifră din coadă va fi maximul C
   3. Afișează la ieșire cifra C.
   4. Elimină cifra C din coadă.

Tema 20

Ambele probleme de la temă cer calculul numărului minim/maxim obținut după eliminarea unor cifre. Genul acesta de prelucrare, eliminarea unor cifre ale unui număr astfel încât numărul rămas să fie maxim (sau minim) apare des la olimpiade.

Să se rezolve următoarele probleme (program C trimis la NerdArena):

• Maxim în fereastră glisantă
• Cuburi dată la ONI 2012 clasa a 8-a. Ea cere eliminarea unui număr mic de cifre, totdeauna 3, ceea ce înseamnă că nu suntem obligați să implementăm o coadă dublă pentru a o rezolva, putem calcula minimul prin forță brută.
• Maxim dată la ONI 2007 clasa a 5-a. Este o problemă de clasa a 5-a la origine, adaptată pentru clasa a 7-a. Rezolvați-o folosind algoritmul din lecție.

Observații:

Atenție: rezolvarea voastră la problema maxim trebuie să folosească o coadă dublă și algoritmul de mai sus. Scopul este să învățăm să implementăm coada dublă.

Notă: cei cărora le plac provocările, încercați să rezolvați problema maxim cu memorie O(Σ), unde Σ este numărul de cifre, adică 10. Pentru aceasta trebuie să modificați implementarea cozii duble.

Tema opțională

Să se rezolve următoarele probleme (program C trimis la NerdArena):

• JBird
• Valutar dată la OJI 2019 clasa a 7-a

Accesează rezolvarea temei 21