Clasa a 8-a lecția 1 - 23 sep 2015

From Algopedia
Jump to navigationJump to search

Lecția de astăzi este o recapitulare a cunoștințelor teoretice învățate în primul semestru din anul trecut.

Recursivitate

Plată suma

Moduri plată suma cu monede 1, 2, 5: 

#include <stdio.h>

int mon[3] = { 1, 2, 5 };

int suma( int s, int nrmon ) { // in cite feluri platim s folosind nrmon monede
  if ( nrmon == 0 )            // daca nu mai avem monede
    return 0;                  // nu putem plati (zero moduri de plata)
  if ( s < 0 )                 // o suma negativa nu se poate plati
    return 0;
  if ( s == 0 )                // o suma de zero se plateste intr-un singur fel
    return 1;
  // putem plati in doua feluri de combinatii
  // - fie in combinatii care se termina cu ultima moneda din vector
  // - fie in combinatii care nu folosesc deloc ultima moneda din vector
  return suma( s - mon[nrmon - 1], nrmon ) + suma( s, nrmon - 1 );
}

int main() {
  int s;

  scanf( "%d", &s );
  printf( "%d este platibila in %d moduri\n", s, suma( s, 3 ) );
  return 0;
}

Tipuri de recursie

Există două moduri de implementare a unei soluții recursive:

Recursie Top-Down

Recursie Top-Down: cînd pornim cu o problemă mai mare și apelăm funcția pentru probleme mai mici pe care le folosim ulterior în apelul curent. În subproblema de bază returnăm un rezultat de bază, cum ar fi zero sau unu. În această categorie sînt toate exemplele de mai sus cu excepția combinărilor, permutărilor si sumei de monede.

Factorial

Funcția factorial implementată recursiv top-down:

Ne vom folosi de definiția recursivă: 

int fact( int n ) {
  if ( n == 1 )
    return 1;
  else
    return n * fact( n - 1 );
}

Recursie Bottom-Up

Recursie Bottom-Up: cînd pornim cu o problemă mai mare și cu un acumulator de soluție, care inițial este vid (zero sau unu), iar în apelurile ulterioare reducem mărimea problemei adăugînd (construind) soluția finală în acumulator. Exemplele de combinări și permutări sînt Bottom-Up în care acumulatorul este vectorul și nu este transmis în mod explicit, deși am putea face acest lucru.

Factorial

Funcția factorial implementată recursiv bottom-up cu acumulator: 

#include <stdio.h>

int fact( int n, int ac ) {
  if ( n == 1 )                 // cind n = 1 am terminat calculul in ac
    return ac;
  else
    return fact( n - 1, n * ac ); // adaugam n la acumulator
}

int main() {
  int n;

  scanf( "%d", &n );
  printf( "%d! = %d\n", n, fact( n, 1 ) );

  return 0;
}

Fill recursiv (flood fill)

Introducere

Algoritmul fill "umple" toate golurile accesibile de la un punct dat. Golurile pot fi elemente zero intr-o matrice, de exemplu, iar vecinii pot fi definiți ca elementele adiacente pe linie și coloană (acesta este cazul cel mai întîlnit). Alteori vecinii pot fi definiți ca avînd un punct comun cu elementul curent, ceea ce include și elementele alăturate pe diagonală. Să luăm un exemplu clasic:

Se dă o matrice a[m][n] cu elemente 0 și 1, 0 semnificînd liber și 1 semnificînd zid, precum și o poziție în matrice, (l, c). Să se spuna cîte elemente 0 sînt accesibile de la (l, c) avansînd doar pe linie sau pe coloană. 

int suma;
...
void fill( int l, int c ) {
  suma++;
  a[l][c] = 1;
  if ( l > 0 && a[l-1][c] == 0 )
    fill( l - 1, c );
  if ( l < m-1 && a[l+1][c] == 0  )
    fill( l + 1, c );
  if ( c > 0 && a[l][c-1] == 0  )
    fill( l, c - 1 );
  if ( c < n-1 && a[l][c+1] == 0  )
    fill( l, c + 1 );
}
...
int main() {
  ...
  suma = 0;
  if ( a[l][c] == 0 )
    fill( l, c );
  printf( "%d", suma );
  ...
}

Acest algoritm are complexitate O(m×n) ca timp, deoarece poate parcurge toate elementele matricei, iar prelucrarea per element este O(1). Memoria ocupată este de asemenea O(m×n) deoarece fiecare apel recursiv necesită O(1) memorie și putem avea O(m×n) apeluri recursive unul în altul.

Atenție! Acesta este principalul impediment al metodei! Ea folosește foarte multă memorie suplimentară.

Liste

Definiție

Definiție: în informatică o listă înlănțuită este o structură de date care constă dintr-un grup de noduri care împreună reprezintă o secvență. În forma ei cea mai simplă fiecare nod este format din date și o referință (înlănțuire) către nodul următor în secvență. Lista înlănțuită permite inserarea și ștergerea eficientă a elementelor de pe orice poziție în secvență.

Exemplu de listă înlănțuită

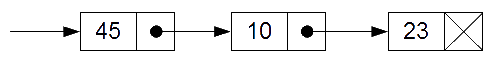
Implementare

O primă implementare posibilă este folosind doi vectori: un vector v care memorează elementele listei (numere întregi de exemplu) și un vector next, care memorează indicele următorului element din listă. Perechea (v[i], next[i]) conține un nod al listei.

Operații cu liste

Inserare

Inserare element - concept
Inserare element - implementare
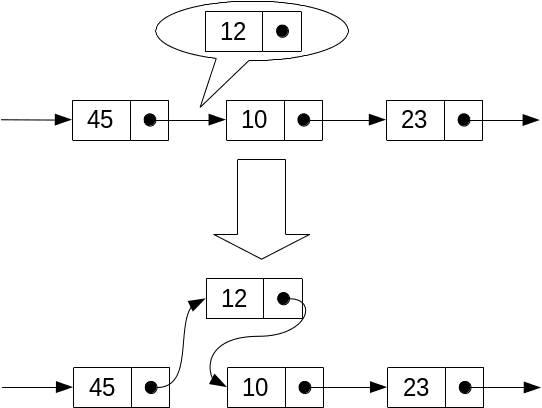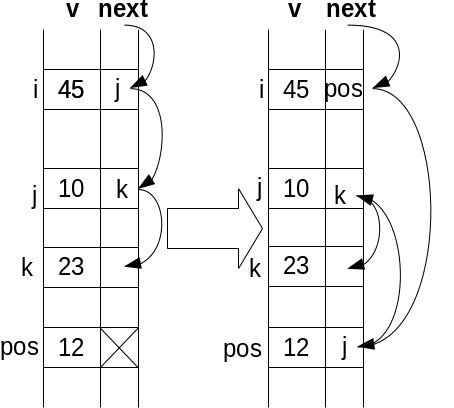// pos conține poziția nodului de inserat
next[pos] = next[i];
next[i] = pos;
Inserare element în listă după elementul i

Ștergere

Ștergere element - concept
Ștergere element - implementare
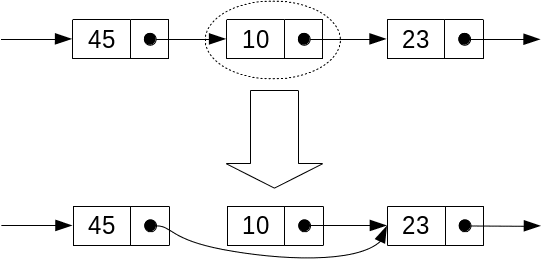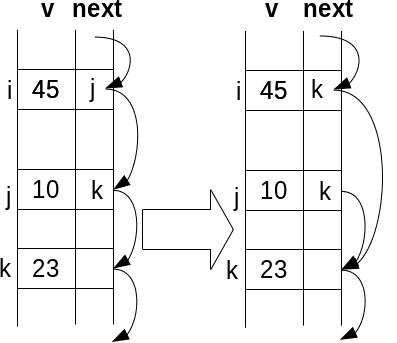next[i] = next[next[i]];
Ștergere element din listă după elementul i

Structuri de date abstracte

Stiva

Stiva este o structură de date elementară care menține intern o listă de elemente. Inițial această listă este vidă. Asupra listei se pot efectua doar următoarele operații:

  • push(value) - inserează o valoare dată la sfârșitul listei;
  • top - returnează valoarea de la sfârșitul listei;
  • pop - șterge valoarea de la sfârșitul listei.

Coada

Coada este o structură de date elementară care menține intern o listă de elemente. Inițial această listă este vidă. Asupra listei se pot efectua doar următoarele operații:

  • push(value) - inserează o valoare dată la sfârșitul listei;
  • front - returnează valoarea de la începutul listei;
  • pop - șterge valoarea de la începutul listei.

Deque

Deque este o structură de date elementară care menține intern o listă de elemente. Inițial această listă este vidă. Asupra listei se pot efectua doar următoarele operații:

  • push_front(value) - inserează o valoare dată la începutul listei;
  • push_back(value) - inserează o valoare dată la sfârșitul listei;
  • pop_front - șterge valoarea de la începutul listei;
  • pop_back - șterge valoarea de la sfârșitul listei;
  • front - returnează valoarea de la începutul listei;
  • back - returnează valoarea de la sfârșitul listei.

Analiza amortizată

Despre analiza amortizată. Citat din CLR: În analiza amortizată facem media timpului necesar pentru a executa o secvență operații, împărțindu-l la toate operațiile executate. Prin analiza amortizată putem să arătăm că costul mediu al unei operații este mic, atunci cînd împărțim la numărul de operații, cu toate că o singură operație din secvență ar putea fi "scumpă". Acest cost mediu per operație se mai numește și costul amortizat.

Problema bibliotecarului (coada implementată cu două stive)

Un bibliotecar primește cărți una cîte una și le returnează în aceeași ordine, la cerere. În spatele ghișeului el are doi subalterni. Bibliotecarul trebuie să dea cărțile primite unuia din subalterni. Poate de asemenea să ceară înapoi cărți de la subalterni. Fiecare subaltern ține o stivă de cărți. Atunci cînd bibliotecarul îi dă o carte subalternul o pune peste toate celelalte, în stiva sa. Atunci cînd bibliotecarul îi cere o carte o ia pe prima din stivă și i-o returnează. Voi trebuie să găsiți algoritmul de funcționare a bibliotecarului astfel încît după un număr mare de depuneri și cereri de cărți numărul total de operații (înmînări de cărți) să fie cît mai mic ca complexitate. Puteți presupune că vor fi 500000 de depuneri de cărți și 500000 de cereri, în orice ordine coerentă.

Rezolvarea directă, evidentă, este, surprinzător, și cea corectă: bibliotecarul va da toate cărțile primite subalternului 1. Cînd i se cere o carte, i-o va cere subalternului 2. Dacă subalternul 2 nu are cărți atunci el îi va cere, pe rînd cărți subalternului 1 și i le va da subalternului 2, pînă ce subalternul 1 nu mai are cărți. Apoi returnează cartea pe care i-o va da subalternul 2.

Funcționează corect acest algoritm? Desigur, urmăriți un exemplu și vă veți convinge. Dar pare foarte ineficient! Pentru o carte cerută este posibil ca bibliotecarul să facă n operații! Să facem același calcul ca și mai devreme: orice carte va fi depusă la primul subaltern, apoi scoasă și depusă la cel de-al doilea subaltern și apoi returnată. Drept pentru care numărul total de operații va fi 3n, iar costul amortizat al unei operații de depunere sau de scoatere va fi O(1).

Maximum în fereastră glisantă (maximum over a sliding window)

  • Enunț: dîndu-se un șir de n numere considerăm cele n – k + 1 subsecvențe de k numere consecutive în șir (denumite și "ferestre" de lungime k). Putem vedea aceste ferestre ca pe o singură fereastră, deplasabilă, care ne dă acces la k elemente din vector odată. Se cere ca pentru fiecare fereastră să se găsească maximul.
  • Algoritmul de rezolvare trivial (forță brută) recalculează maximul pentru fiecare din ferestre, avînd complexitate O(kn).
  • Pentru a reduce complexitatea găsirii maximului procedăm astfel: luăm prima fereastră, de la 0 la k-1. Să spunem că maximul se află pe poziția p1. Pe măsură ce vom deplasa fereastra este imposibil ca elementele din-naintea maximului să fie vreodată maximul ferestrei, deoarece ele vor face parte împreună cu maximul din această fereastră. Să considerăm poziția celui mai mare element după maxim și la dreapta lui, în fereastră. Fie ea p2. Rezultă că nici un element pe pozițiile intermediare i, p1 < i < p2, nu poate fi vreodată maxim în fereastră, deoarece aceste elemente vor fi împreună cu p2 în toate ferestrele care le conțin. Similar, considerînd p3 poziția următorului maxim, nici un element între p2 și p3 nu va putea fi maxim. Astfel apare următorul algoritm:
    • Memorăm toate maximele descrescătoare din prima fereastră, într-o coadă. Primul element din coadă este maximul ferestrei.
    • Cînd deplasăm fereastra trebuie să actualizăm structura de maxime din coadă. Pentru aceasta dăm atenție elementului care dispare din fereastră și celui care intră în fereastră.
    • Dacă elementul care iese nu este maximul curent, nu avem nimic de făcut.
    • Dacă este maximul curent vom scoate primul element din coada de maxime.
    • Dacă elementul proaspăt adăugat în fereastră este mai mic decît ultimul maxim din coadă se adaugă la coadă. În caz contrar el va "arunca" ultimul element, iar și încercăm din nou adăugarea în coadă.
    • Rezultă că noul element din fereastră "aruncă" toate elementele de la urma cozii strict mai mici ca el, iar apoi îl adăugăm normal la coadă.
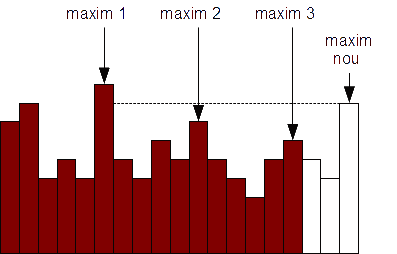
      În figură noul maxim va elimina din coadă maximele 2 și 3. Coada rămasă va conține maximul 1 și maximul nou
  • La prima vedere pare că acest algoritm are complexitate O(kn). Folosind analiza amortizată putem calcula complexitatea reală ca fiind O(n).
  • Memoria suplimentară folosită este mărimea maximă a cozii, adică O(k).
  • Observăm că putem folosi acest algoritm la problema cuburi. Genul acesta de prelucrare, eliminarea unor cifre ale unui număr astfel încît numărul rămas să fie maxim (sau minim) apare des la olimpiade.
  • La temă aveţi şi problema maxim, o problemă de clasa a 5a la origine, adaptată pentru clasa a 8a şi analiză amortizată. Pentru cei cărora le plac provocările, încercaţi să rezolvaţi problema cu memorie O(1).

Temă

Pentru data viitoare va trebui să rezolvați două probleme:

Retrieved from "https://www.algopedia.ro/wiki/index.php?title=Clasa_a_8-a_lecția_1_-_23_sep_2015&oldid=12569"