Clasa a IX-a lecția 19 - 21 mar 2020
Clasament teme lecțiile 1 - 18
Pe categorii
Divizori / Primalitate / Ciur
Sortari
Matrici
Cautare binara
Stivă
Recursivitate
Generale
Concursuri
Lecție
De acasă
Având în vedere că ne aflăm în situația de a nu putea ține cercul fizic, vă invit totuși pe fiecare dintre voi să treceți prin lecțiile pe care vi le pregătesc și să participați la concursuri și să lucrați temele pe care vi le propun.
Recursivitate (Flood Fill)
După cum îi spune și numele, algoritmul Flood Fill "inundă" sau "umple" toate golurile accesibile dintr-un anumit punct.
Exemplu Avem o matrice plină de valori 0 și 1, unde 0 înseamnă loc liber iar 1 înseamnă obstacol. Avem un omuleț care se află în căsuța liberă de la poziția (i, j) din matrice. Omulețul nostru se poate muta într-o căsuță alăturată în oricare din cele 4 direcții (N, S, E, V), dacă este liberă. Vrem să numărăm câte căsuțe îi sunt accesibile.
Soluție Pornim o funcție recursivă din punctul (i, j), care va parcurge și se va apela pentru toți vecinii liberi punctului curent, contorizându-i în același timp.
int sum = 0;
void fill(int l, int c) { // sunt la pozitia l, c
++sum; // contorizez punctul curent
a[l][c] = 1; // marchez pozitia ca fiind parcursa deja / obstacol
if (l > 0 && a[l - 1][c] == 0) // ma deplasez in Nord
fill(l - 1, c);
if (l < m - 1 && a[l + 1][c] == 0) // ma deplasez in Sud
fill(l + 1, c);
if (c > 0 && a[l][c - 1] == 0) // ma deplasez in Vest
fill(l, c - 1);
if (c < n - 1 && a[l][c + 1] == 0) // ma deplasez in Est
fill(l, c + 1);
}Exemplificare grafică
Sursă: IQAcademy
Să vedem niște vizualizări ale algoritmului flood fill preluate de la wikipedia: algoritm flood fill:


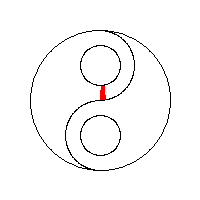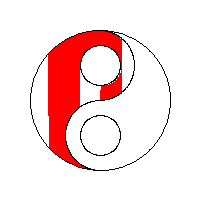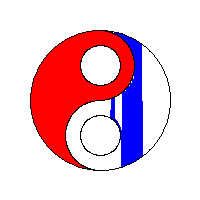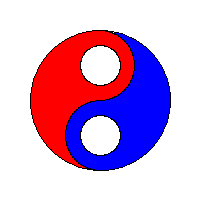
Optimizare: bordare matrice
O optimizare clasică care ajută mai ales în claritatea codului este bordarea matricii. Această tehnică reprezintă împrejmuirea matricii cu obstacole. Mai precis, în funcție de datele de intrare, trebuie găsită o valoare cu care să se umple linia 0, coloana 0, linia m + 1 și coloana n + 1 a matricii. Astfel nu mai este nevoie să întrebăm dacă vecinul către care ne îndreptăm este sau nu în matrice.
int sum = 0; // sum este initial 0, declarata global
void fill(int l, int c) { // sunt la pozitia l, c
++sum; // contorizez punctul curent
a[l][c] = 1; // marchez pozitia ca fiind parcursa deja / obstacol
if (a[l - 1][c] == 0) // ma deplasez in Nord
fill(l - 1, c);
if (a[l + 1][c] == 0) // ma deplasez in Sud
fill(l + 1, c);
if (a[l][c - 1] == 0) // ma deplasez in Vest
fill(l, c - 1);
if (a[l][c + 1] == 0) // ma deplasez in Est
fill(l, c + 1);
}
...
int main() {
...
for (j = 0; j <= n + 1; ++j) {
a[0][j] = 1; // bordez linia 0
a[m + 1][j] = 1; // bordez linia m + 1
}
for (i = 0; i <= m + 1; ++i) {
a[i][0] = 1; // bordez coloana 0
a[i][n + 1] = 1; // bordez coloana n + 1
}
...
}Atenție Trebuie să avem grijă să declarăm matricea suficient de mare pentru a face loc acestei bordări.
Extindere la 8 vecini
Este evident că acest algoritm se poate extinde ușor și în cazul în care omulețul nostru poate parcurge toate cele 8 direcții: N, S, E, V, NE, NV, SE, SV.
Quick tip: vectori de direcție
Nu este o optimizare, dar poate oferi claritate codului prin evitarea repetărilor, mai ales în cazul în care avem de apelat aceeași funcție pentru 8 direcții diferite. Vom declara doi vectori cu valori implicite în care vom reține diferențele necesare pentru a ne deplasa în toate direcțiile în care dorim:
int dirl[] = {-1, 0, 1, 0};
int dirc[] = { 0, 1, 0, -1};
int sum = 0; // sum este initial 0, declarata global
void fill(int l, int c) { // sunt la pozitia l, c
++sum; // contorizez punctul curent
a[l][c] = 1; // marchez pozitia ca fiind parcursa deja / obstacol
for (d = 0; d < 4; ++d) // parcurg cele 4 directii
if (a[l + dirl[d]][c + dirc[d]] == 0) // daca este liber
fill(l + dirl[d], c + dirc[d]); // deplasez
}Complexitate
Complexitate timp: O(M * N), fiecare poziție fiind vizitată cel mult o dată
Complexitate spațiu: O(M * N) suplimentar! Adică, pe lângă matricea pe care o avem deja în memorie, deoarece trebuie să reținem și stiva de recursie
Aplicații
Lucrați secțiunea Aplicații, citiți problemele și explicațiile.
Temă
oras - varena
enclave - varena
Participați la concursul de săptămâna viitoare, îl voi face public și vă voi anunța cât de curând pe Slack.