Clasa a IX-a lecția 31
Matrice patratica
O matrice patratica este o matrice in care numarul de linii este egal cu numarul de coloane ( n = m )
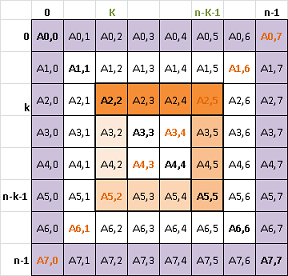
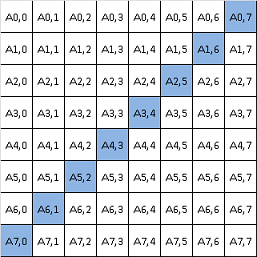
Parcurgerea diagonalei principale
 |
for( i = 0; i < n; i++ )
printf ( "%d ", a[i][i] );Aplicatie: Suma elementelor de pe diagonala principala
s = 0;
for( i = 0; i < n; i++ )
s += a[i][i];
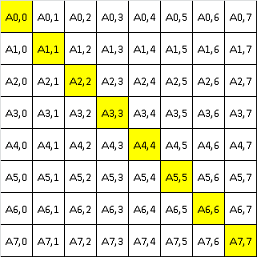
printf ( "%d", s );Parcurgerea diagonalei secundare
 |
for ( i = 0; i < n; i++ )
printf ( "%d ", a[i][n-i-1] );Aplicatie: Cate numere pare sunt pe diagonala secundara
int cnt = 0;
for (i = 0; i < n; i++ )
if ( a[i][n-i-1] % 2 == 0)
cnt ++;
printf ( "%d ", cnt );// fara if
int cnt = 0;
for (i = 0; i < n; i++ )
cnt += ( 1 - a[i][n-i-1] % 2 ) ;
printf ( "%d ", cnt );// fara if
int cnt = 0;
for (i = 0; i < n; i++ )
cnt += a[i][n-i-1] % 2 ; // numaram imparele
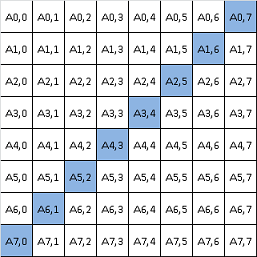
printf ( "%d ", n - cnt );Elemente de deasupra si de sub diagonala principala
 |
//Parcurgerea elementelor de deasupra diagonalei principale
for ( i = 0; i < n; i++ )
for ( j = i + 1; j < n; j++ )
printf ( "%d ", a[i][j] );//Parcurgerea elementelor de sub diagonala principala
for ( i = 0; i < n; i++ )
for ( j = 0; j < i; j++ )
printf ( "%d ", a[i][j] );Aplicatie
Cate elemente distincte sunt deasupra diagonalei principale. Matricea are ca elemente valori intre 1 si 1000. Dimensiunea matricei este 1<n<= 100
for ( i = 0; i <= 1000; i++ )
v[i] = 0;
for ( i = 0; i < n; i++ )
for ( j = i + 1; j < n; j++ )
v[a[i][j]]++;
cnt = 0;
for( i = 0; i <= 1000; i++)
if( v[i] != 0 )
cnt++;
cout << cnt;// mai elegant :)
for ( i = 0; i <= 1000; i++ )
v[i] = 0;
for ( i = 0; i < n; i++ )
for ( j = i + 1; j < n; j++ )
v[a[i][j]] = 1;
cnt = 0;
for( i = 0; i <= 1000; i++)
cnt += v[i];
cout << cnt;Elemente de deasupra si de sub diagonala secundara
 |
//Parcurgerea elementelor de deasupra diagonalei secundare
for (i=0;i<n;i++)
for (j=0; j < n-i-1; j++ )
printf ("%d ", a[i][j]);//Parcurgerea elementelor de sub diagonala secundara
for (i = 0; i < n; i++ )
for ( j = n-i; j < n; j++ )
printf ( "%d ", a[i][j] );Aplicatie: Produsul elementelor nenule de deasupra diagonalei secundare
long long p = 1;
for ( i = 0; i < n; i++ )
for (j = 0; j < n - i - 1; j++ )
if( v[i][j] )
p *= v[i][j];
printf("%lld", p);Aplicatie: Cate numere prime sunt sub diagonala secundara
contor = 0;
for (i = 0; i < n; i++ )
for ( j = n - i; j < n; j++ ){
//verificam daca a[i][j] este prim
d = 2;
while ( d * d < a[i][j] && a[i][j] % d != 0 )
d++;
if ( d * d == a[i][j] )
contor ++;
}
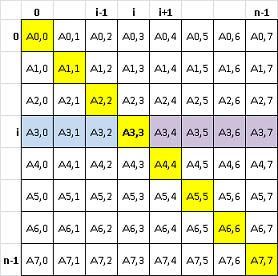
printf ( "%d", contor );Oglindire matrice fata de diagonala principala
- Temă în clasă
Matsim: se dă o matrice pătrată, să se modifice astfel încît în final elementele ei să fie oglindite față de diagonala principală. Diagonala principală e cea care începe în colțul din stînga-sus și se termină în colțul din dreapta-jos. Această operațiune se mai numește si transpunere.
for ( i = 1; i < n; i++ )
for ( j = 0; j < i; j++ ) {
aux = a[i][j];
a[i][j] = a[j][i];
a[j][i] = aux;
}Matsim1 Aceeași problemă pentru diagonala secundară. Diagonala secundară e cea care începe în colțul din dreapta-sus și se termină în colțul din stînga-jos
for ( i = 0; i < (n - 1); i++ )
for ( j = 0; j < (n - i); j++ ) {
aux = a[i][j];
a[i][j] = a[n - 1 - j][n - 1 - i];
a[n - 1 - j][n - 1 - i] = aux;
}Parcurgerea zonelor delimitate de cele 2 diagonale #1749 Zona4
Considerăm o matrice pătratică cu N linii și N coloane. În această matrice sunt definite 4 zone:
- zona 1, formată din elementele situate strict deasupra diagonalei principale și strict deasupra diagonalei secundare;
- zona 2, formată din elementele situate strict deasupra diagonalei principale și strict sub diagonala secundară;
- zona 3, formată din elementele situate strict sub diagonala principală și strict sub diagonala secundară;
- zona 4, formată din elementele situate strict sub diagonala principală și strict deasupra diagonalei secundare;
Se dă o matrice pătratică și un număr natural Z, reprezentând o zonă din matrice. Să se determine suma elementelor din zona Z.
 |
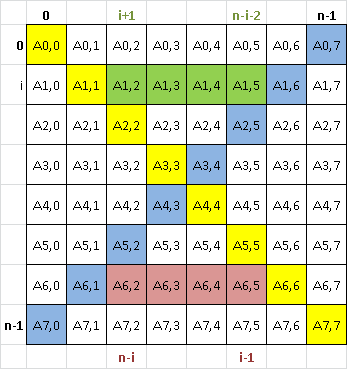| Problema se reduce la a afisa pe rand elementele diagonalelor. avem 2n-1 diagonale. |
Teorie
Rezolvati urmatoarele probleme de pe pbinfo.ro: Zone1 , MedPoz , MatSim1 , Diagonale1 , Diagonale , Chenar , MatSim , CmmdcSum , Zona4 ; Optional: decodificare , Iceberg
Diagonale
Se dă o matrice cu n linii şi n coloane şi elemente numere naturale. Calculaţi diferenţa în valoare absolută dintre sumele elementelor de pe cele două diagonale.
#783 Diagonale1
Se dă o matrice cu n linii şi n coloane şi elemente numere naturale. Să se determine suma elementelor de pe cele două diagonale vecine cu diagonala principală.
#780 CmmdcSum
Se dă o matrice cu n linii şi n coloane şi elemente numere naturale. Calculaţi cel mai mare divizor comun al sumei elementelor de deasupra diagonalei principale și al sumei elementelor de sub diagonala principală.
#786 MatSim
Se dă o matrice cu n linii şi n coloane şi elemente numere naturale. Să se construiască o matrice care să fie simetrica față de diagonala principală a matricei date.
#787 MatSim1 ( discutata in clasa )
Se dă o matrice cu n linii şi n coloane şi elemente numere naturale. Să se construiască o matrice care să fie simetrica față de diagonala secundară a matricei date.
#1749 Zona4 ( discutata in clasa )
Considerăm o matrice pătratică cu N linii și N coloane. În această matrice sunt definite 4 zone:
zona 1, formată din elementele situate strict deasupra diagonalei principale și strict deasupra diagonalei secundare; zona 2, formată din elementele situate strict deasupra diagonalei principale și strict sub diagonala secundară; zona 3, formată din elementele situate strict sub diagonala principală și strict sub diagonala secundară; zona 4, formată din elementele situate strict sub diagonala principală și strict deasupra diagonalei secundare; Se dă o matrice pătratică și un număr natural Z, reprezentând o zonă din matrice. Să se determine suma elementelor din zona Z.
#781 Zone1
Se dă o matrice cu n linii şi n coloane şi elemente numere naturale. Să se afişeze, în ordine crescătoare, sumele elementelor din cele patru zone delimitate de diagonale.
MedPoz
Se dă o matrice cu elemente numere întregi. Să se determine media aritmetică a elementelor strict pozitive din matrice, care sunt situate sub diagonala principală.
LABORATOR
Rezolvati urmatoarele probleme de pe pbinfo:
Spirala , LinColEgale , Zona , Zona1 , Matrice6 , Matrice , MinCols1 , modifMat , Spirala1 , Criptare , Serpuire , wisp
Chenar
( Parcurgerea elementelror de pe chenarul unei matrice ) Să se parcurgă în sensul acelor de ceasornic chenarul exterior al unei matrice pătratice.
spirala
Să se parcurgă o matrice pătratică în spirală în sensul acelor de ceasornic.
 |
| Putem observa ca matricea poate fi descompusa in (n+1)/2'' chenare si ca fiecare chenar k poate fi descompus la randul lui in 4 laturi. Putem tipari deci cele 4 laturi, fiind atenti ca elementele comune sa fie parcurse doar odata |
#784 LinColEgale
Se dă o matrice cu n linii şi n coloane şi elemente numere naturale. Să se determine câte elemente ale matricei se află pe linii și coloane de sumă egală.
#81 Matrice
Scrieţi un program care citeşte de la tastatură un tablou bidimensional cu n linii şi n coloane și afişează pe ecran numărul valorilor din tablou care sunt strict mai mari decât toți vecinii lor.
#998 Matrice6
Se consideră o matrice pătratică cu n linii şi n coloane şi elemente numere naturale. Să se modifice matricea în felul următor: toate elementele de pe liniile care conţin valoare maximă din matrice vor fi mărite cu valoarea minimă din matrice.
#729 Zona
Se dă o matrice pătratică cu n linii și n coloane și elemente numere naturale mai mici decât 1000. Să se afișeze în ordine strict crescătoare valorile situate sub diagonala principală și deasupra diagonalei secundare. Dacă o valoare apare în zona respectivă de mai multe ori, se va afișa o singură dată.
#782 Zona1
Se dă o matrice pătratică cu n linii și n coloane și elemente numere naturale mai mici decât 1000. Să se afișeze în ordine strict crescătoare valorile care apar sub diagonala principală și sub diagonală secundara de cel puţin 2 ori. Fiecare valoare se va afişa o singură dată.
Serpuire
Se dă o matrice cu n linii şi n coloane şi elemente numere naturale. Să se afișeze elementele prin parcurgerea șerpuită a matricei, începând din elementul de pe prima linie și prima coloană, ca în exemplu.
Diagonal
Se citeşte o matrice pătrată de caractere. Să se afişeze două linii de caractere, fiecare linie conţinînd toate caracterele matricei. Prima linie afişată conţine caracterele matricei în parcurgerea pe diagonale paralele cu diagonala principală. A doua linie afişată conţine caracterele matricei în parcurgerea pe diagonale paralele cu diagonala secundară. Diagonala principală este din coţul stînga sus în colţul dreapta jos. Diagonala secundară este din colţul dreapta sus, în colţul dreapta jos. Atenţie! Fişierul de intrare conţine numai matricea de caractere, fiecare linie terminîndu-se cu '\n'. Nu se dă n, dimensiunea matricei, trebuie sa o deduceţi.
 |
 |
 |
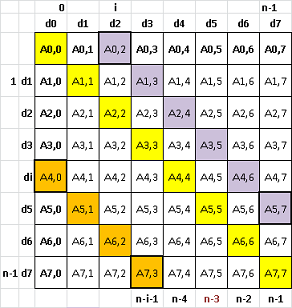| Problema se reduce la a afisa pe rand elementele diagonalelor. avem 2n-1 diagonale. |
MinCols1
Se dă o matrice cu elemente numere naturale. Să se determine ultima cifră a produsului elementelor de pe diagonala secundară cu proprietatea că sunt minime pe coloanele lor.
- Spirala1 (pbinfo)
Se dau n numere naturale, un n este un pătrat perfect. Să se construiască în memorie o matrice pătratică cu toate cele n numere, în spirală, în sens invers acelor de ceas astfel: pe prima coloană, începând cu linia 1, se vor trece primele elemente din şir (de sus în jos), apoi pe ultima linie, începând de la prima coloană până la ultima (de la stânga la dreapta), apoi pe ultima coloană, de la ultima linie la prima (de jos în sus), apoi pe prima linie, de la ultima coloană la prima (de la dreapta la stânga) şamd.
#1487 decodificare
Scrieţi un program care, citind din fişierul de intrare şirul de caractere cod(s), execută operaţia de decodificare şi afişează textul iniţial s (care a fost codificat) în fişierul de ieşire.
#1451 Iceberg
Se dă o matrice reprezentând o zonă dintr-un ocean ce conține un iceberg; valorile egale cu 1 fac parte din iceberg, iar cele egale cu 0 reprezintă apă.
Se știe că icebergul este înconjurat de apa (nu există nici o valoare de 1 pe marginea matricei) și că într-un interval de timp se topesc toate zonele icebergului care au cel puțin doua laturi vecine cu apa.
Determinați și afișați cate intervale de timp sunt necesare ca icebergul să se topească în întregime. De asemenea, afișați pentru fiecare interval de timp câte poziții de gheață are icebergul la începutul intervalului.
Tema Laborator
Rezolvati problemele din fisa de la laborator ramase nerezolvate
- diagonal - parcurgerea elementelor unei matrice
- zoomx2 - generare matrice pe baza unei matrice date
- căutare - cautare submatrice in matrice
criptare, modifMat , Criptare , wisp, Optional: decodificare , Iceberg
