Introducere

Prezentarea instructorului

Numele meu este Teodor Plop și voi susține acest curs de informatică. Sunt un fost elev al liceului Tudor Vianu, sunt pasionat de programare, grafică și jocuri pe calculator iar de mai bine de 5 ani de zile lucrez ca programator în industria jocurilor din România.

Prezentarea cercului

Cercul are ca scop dezvoltarea gândirii algoritmice și logice, punerea bazelor informaticii și aprofundarea ei la cel mai înalt nivel, incluzând evident și materia de olimpiadă. Pentru a da o șansă și celor care nu au avut tangență cu informatica pânâ în această clasă, voi incepe informatica de la zero, având câteva lecții de introducere. Țin să îi asigur pe cei care au deja experiență în ale informaticii că au ce învăța de la acest curs și că dificultatea acestuia le va atinge așteptările.

Structura cercului

Vom avea ~3 lecții de introducere în algoritmică, în care vom rezolva probleme folosind scheme logice. Apoi, vom susține un test de selecție în urma căruia se va forma grupa alături de care vom continua cercul, care va conține în mod ideal maxim 15 elevi. Nivelul de performanță al cercului este unul înalt și este imposibil să atingem acest nivel având un număr mare de studenți. Dupa testul de selectie vom intra in limbajul C si in materia propriu-zisa.

Reguli

Cercul este opțional. Eu vă promit că am sa dedic timp și efort în pregătirea voastră. Deci, mă aștept să văd implicare și efort și din partea voastră. Veniți la acest cerc doar dacă vreți să învățați ceva în plus, ceva nou, ceva ce vă place suficient de mult încât sa fiți serioși și dedicați. Nu vă ține nimeni cu forța aici și singurul lucru pe care îl obtineți dacă veniți contra voinței proprii este timp pierdut.

Acestea fiind spuse, regulile cercului:

Prezența
- Prezența este obligatorie
Seriozitate, implicare & dorința de a învăța
- Tratați cercul cu seriozitate
- Aveți o atitudine pozitivă (Pot și vreau să fac asta!)
- Temele sunt obligatorii

Grup de discuții

Am creat un grup de Slack la care înscrierea este obligatorie pentru cei care vin la cercul de informatică, și opțională pentru ceilalți. Vom folosi grupul în două scopuri:

Pentru a face anunțuri oficiale.
Pentru a vă corecta temele și a vă oferi sfaturi individual.

Veți primi invitații pe adresele voastre de mail.

Lecție

Algoritmi

Definiție

Algoritm = set de instrucțiuni sau reguli care, pornind cu un set de date inițiale, rezolvă o clasă de probleme folosind operații precise, executate mecanic, fără intervenția creativă a omului.

Exemple

Rețete de bucate, instrucțiuni asamblare IKEA, ...

Proprietăți

Precizie - Sau neambiguitate. Fiecare pas trebuie să fie neambiguu și executabil fără intervenție creativă.
Generalitate - Să rezolve o clasă de probleme, nu doar o problemă în particular.
Finitudine - Algoritmul trebuie să se termine în timp finit. Din punct de vedere practic trebuie să se termine într-un timp rezonabil.
Corectitudine - Rezultatul final trebuie să fie corect pentru toate datele de intrare.

Scheme logice

Schemele logice sunt un mod de descriere a algoritmilor (un alt mod este pseudocodul). Ele conțin următoarele blocuri:

Bloc de calcul
Bloc de citire sau scriere
Bloc de decizie
Bloc terminator

Bloc terminator

Singurul rol al acestui bloc este de a marca începutul și sfârșitul algoritmului. Iată cele două blocuri pe care le vom folosi:

este locul unde începe schema logică.
este locul unde se termină schema logică.

Bloc de citire/scriere

Aceste blocuri controlează fluxul de date către și dinspre algoritmul nostru.

Citire = furnizăm algoritmului setul de date inițial de care are nevoie pentru a rezolva problema.
Scriere = algoritmul ne întoarce rezultatele.

Exemple:

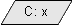citește o valoare și o depozitează în x. 'C' vine de la 'citește'.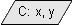
citește două valori, una ce va fi depozitată în x iar a doua în y.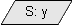
scrie valoarea stocată în y. 'S' vine de la 'scrie'.

Bloc de calcul

Așa cum sugerează și numele, aceste blocuri sunt folosite pentru a calcula expresii. De obicei conțin calcule matematice. Exemple:

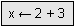calculează expresia 2 + 3 și stochează rezultatul (în acest caz 5) în x.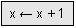
ia vechea valoare a lui x x, îi adună 1 și stochează rezultatul în variabila x, suprascriind vechea valoare. Dacă x era 5 inițial, valoarea finală va fi 6, după execuția acestui bloc.

Bloc de decizie

Un bloc de decizie este folosit în momentul în care vrem să acționăm diferit în funcție de o anumită expresie. Dacă expresia este adevărată execuția algoritmului continuă pe ramura din dreapta. Dacă expresia este falsă execuția continuă cu ramura din stînga. Putem considera că acest bloc "pune o întrebare". Dacă răspunsul întrebării este pozitiv, algoritmul se continuă cu ramura din dreapta. Dacă răspunsul este negativ, cu ramura din stânga.

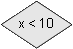testează dacă x este mai mic ca zece, atunci cînd se ajunge în acest punct al algoritmului. Dacă x este mai mic ca zece continuăm cu blocurile de pe ramura dreaptă. Dacă x este mai mare ca zece, sau egal cu zece, continuăm cu ramura din stînga.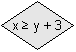
testează dacă valoarea lui x este mai mare sau egală cu valoarea lui y plus 3. În acest caz continuăm pe ramura din dreapta. Dacă nu, continuăm pe ramura din stânga.

Exemplu: distanța până la Stormwind

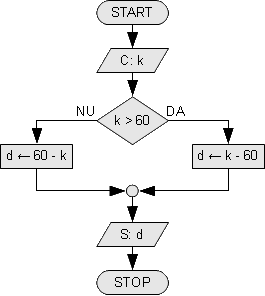
Orașul Stormwind se află pe autostrada A1 la kilometrul 60. Se știe că noi ne aflăm pe autostradă la kilometrul k (k citit). La ce distanță de Stormwind ne aflăm? Să construim o schemă logică care o calculează (vezi figura de mai jos).

Pentru a executa o schemă logică pornim de la blocul de START si urmăm săgețile. Primul pas este să citim k, kilometrul la care ne aflăm pe autostradă. Apoi vom testa dacă am depășit Stormwind, adică dacă am trecut de kilometrul 60. Dacă k este mai mare decît 60 o vom lua pe ramura din dreapta, numită și ramura DA, unde vom calcula distanța d ca fiind valoarea k - 60. Dacă k este mai mic sau egal cu 60 vom urma ramura din stînga (ramura NU) unde vom calcula distanța ca fiind 60 - k. Indiferent ce ramură am urmat vom ajunge în final la conectorul cerculeț. În acest moment d conține valoarea corectă a distanței. Tot ce mai avem de făcut este să o afișăm, după care ne oprim la blocul STOP.

Programarea structurată

Programarea structurată este un mod de a scrie scheme logice care îmbunătățește claritatea, citibilitatea, calitatea și ușurința modificării ulterioare. Denumirea vine de la Programarea cu structuri. Mai exact, programarea structurată ne limitează modul în care putem folosi și îmbina blocurile. Ele pot fi aranjate în trei feluri distincte, conform unor modele numite structuri. În continuare vom studia două dintre aceste structuri.

Structura liniară

Se mai numește și structură de calcul. Ea constă dintr-o înșiruire de blocuri de calcul și blocuri de citire/scriere.

Structura alternativă

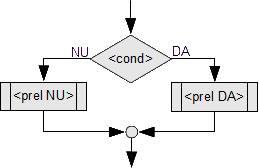
Structura alternativă este compusă dintr-un bloc de decizie, două ramuri de execuție, DA și NU, care se reunesc la final.

Operatori

Vom enumera principalii operatori pe care îi vom folosi în scheme logice.

Operatori aritmetici

Operatorii aritmetici pe care îi putem folosi în blocurile de calcul sunt:

Operator	Semnificație	Exemplu
`+`	Adunarea a două numere	`x ← a + b`
`-`	Scăderea a două numere	`y ← y - 10`
`*`	Înmulțirea a două numere	`x ← a * 10`
`/`	Împărțirea întreagă a două numere (cîtul împărțirii)	`x ← 14 / 3` (`x` primește valoarea 4)
`%`	Împărțirea întreagă a două numere (restul împărțirii)	`x ← 14 % 3` (`x` primește valoarea 2)
`( )`	Paranteze: schimbul ordinii operațiilor	`x ← 2 * (10 - (3 + 4))` (`x` primește valoarea 6)
`__ √`	Radical: partea întreagă a operațiunii radical	`__ x ← √10` (`x` primește valoarea 3)

Operatori de comparație și logici

Operatori de comparație și logici: = ≠ < ≤ > ≥ și sau

Probleme

Strângeri de mînă

Avem n oameni care dau mâna fiecare cu fiecare o singură dată. În total sunt k strângeri de mână. Să se scrie o schemă logică care citește k (numărul de strângeri de mînă), apoi calculează și afișează n (numărul de oameni).

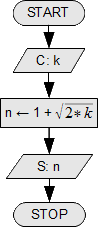
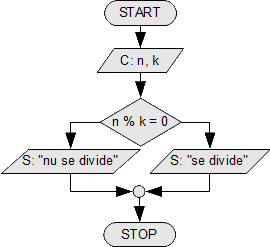
n oameni dau mâna. Sunt k strângeri de mână. Dându-se k să se calculeze n.

Testul de divizibilitate

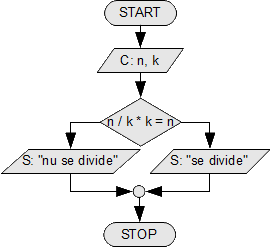
Testul de divizibilitate n cu k, discuție cele două metode, prima folosind operatorul %, a doua folosind operatorul /.

Extragerea ultimei cifre

Să se afișeze ultima cifră a unui număr n, folosind operatorul '%', respectiv restul împărțirii la 10. Am demonstrat că restul împărțirii la 10 este ultima cifră a unui număr.

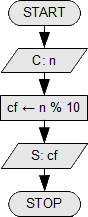
Extragerea primei cifre

Se citește n, un număr natural strict mai mic decît 100. Să se afișeze prima cifră a lui n.

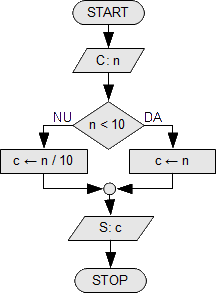
Laturile unui triunghi

Se citesc trei numere, a, b și c. Să se spună dacă pot fi laturile unui triunghi.

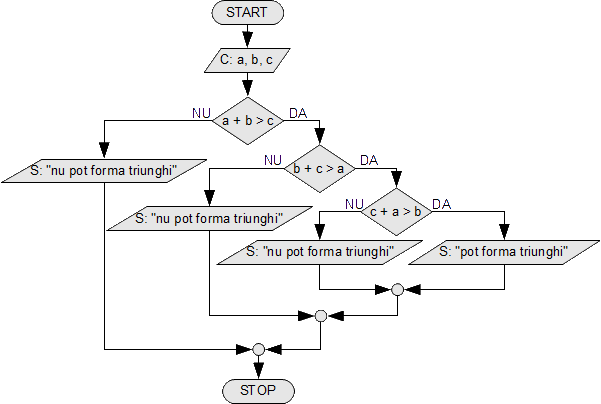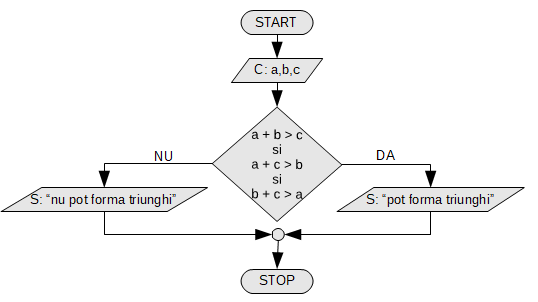a, b, c pot fi laturile unui triunghi? varianta 2

Tema

Scrieți temele pe foi si aduceți-le semnate data viitoare. Vă voi returna tema corectată. Încercați să vă gândiți singuri la răspunsuri, apoi, dacă nu găsiți rezolvarea căutați pe google și abia apoi, dacă nu reușiți, întrebați părinții sau prietenii. Scopul principal al temelor este să învățați să aplicați ce lucrăm la curs, nu să impresionați instructorul sau colegii.

Se dă un număr n între zero și 999 inclusiv. Să se afișeze cifrele lui în ordine inversă.
Să se spună dacă un număr n are ultimele două cifre consecutive, în ordine crescătoare. Exemple: 312, 4523 au cifrele ultimele doua cifre consecutive in ordine crescatoare; 215, 4321 și 7 nu au.
Se dau 3 numere. Să se afișeze maximul dintre ele.
Ecuația de gradul 1: se dau a și b astfel încât a * x = b. Să se determine x pe baza valorilor a și b. Am discutat cele trei cazuri:
- când a este diferit de zero x este b : a.
- când a este zero și b este diferit de zero x nu există.
- când a este zero și b este zero x poate avea orice valoare.
Să se spună dacă n copii se pot așeza în formă de pătrat plin. Exemple:
- Nouă copii se pot așeza în formă de pătrat astfel:
  Nouă copii așezați în formă de pătrat
- 14 copii nu se pot așeza în formă de pătrat:
  14 copii

Clasa a IX-a lectia 1 - 12 oct 2019

Contents