Clasa a V-a lecția 10 - 06 nov 2012

From Algopedia
Jump to navigationJump to search

Tema - verificare

Rezolvări aici [1]

Lecție

Exerciții

Să se scrie schema logică și programul C pentru următoarele exerciții:

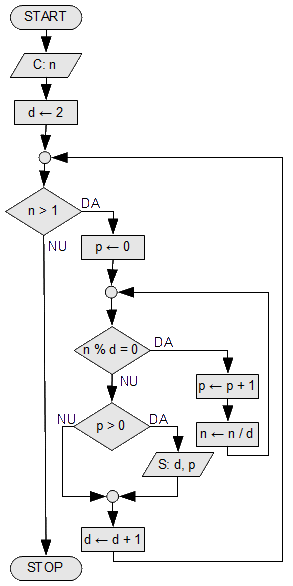
  • Se citește un număr n. Să se descompună în factori primi. Exemple: dacă n = 12 vom afișa 12 = 2^2 * 3; dacă n = 504 vom afișa 504 = 2^3 * 3^2 * 7. Notă de rezolvare: nu este nevoie să testăm dacă un divizor este prim, putem testa toți divizorii. Numai cei primi vor ajunge să dividă n.
Descompunere în factori primi
 
#include <stdio.h>

int main() {
  int n, p, d;

  scanf( "%d", &n );
  printf( "%d =", n );
  d = 2;
  while ( n > 1 ) {
    p = 0;
    while ( n % d == 0 ) {
      p = p + 1;
      n = n / d;
    }
    if ( p > 0 )
      printf( " * %d^%d", d, p );
    d = d + 1;
  }
  printf( "\n" );

  return 0;
}
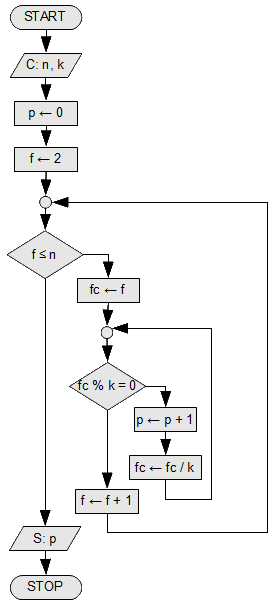
  • Se citesc numerele n și k, k număr prim, k ≤ n. Considerăm numărul n! = 1∙2∙3∙...∙n. Să se afișeze puterea lui k din descompunerea în factori primi a lui n!.
Puterea lui k în n!
 
#include <stdio.h>

int main() {
  int n, k, p, f, fc;

  scanf( "%d%d", &n, &k );
  p = 0;
  f = 2;
  while ( f <= n ) {
    fc = f;
    while ( fc % k == 0 ) {
      p = p + 1;
      fc = fc / k;
    }
    f = f + 1;
  }
  printf( "%d", p );

  return 0;
}

Algoritmul lui Euclid (cmmdc a două numere)

  • Algoritmul lui Euclid este o metodă eficientă de calcul al celui mai mare divizor comun (CMMDC). El este denumit după matematicianul grec Euclid, care l-a inventat. Un avantaj important al algoritmului lui Euclid este că el poate găsi CMMDC eficient fără să trebuiască să calculeze factorii primi ai numerelor.
  • Euclid a observat că CMMDC a două numere a și b rămîne același dacă se scade numărul mai mic din cel mai mare (demonstrați!). Presupunînd că a este numărul mai mare, scăzînd în mod repetat pe b din a, în a va rămîne restul împărțirii lui a la b. Rezultă că CMMDC(a, b) este totuna cu CMMDC(b, a % b). Algoritmul care rezultă este următorul: luăm restul împărțirii lui a la b, apoi restul împărțirii lui b la rest, și așa mai departe, pînă ce obținem un rest zero. CMMDC este numărul rămas.
  • Exemplu: să calculăm CMMDC(252, 105). Calculăm 252 % 105 = 42. De aceea va trebui să calculăm CMMDC(105, 42). În continuare calculăm 105 % 42 = 21. Deci, vom calcula CMMDC(42, 21). Calculăm 42 % 21 = 0. Deoarece restul este zero CMMDC va fi ultimul număr nenul, adica 21.
  • Schema logică și programul:
CMMDC cu algoritmul lui Euclid
 
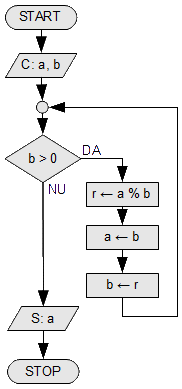#include <stdio.h>

int main() {
  int a, b, r;

  scanf( "%d%d", &a, &b );
  while ( b > 0 ) {
    r = a % b;
    a = b;
    b = r;
  }
  printf( "%d", a );

  return 0;
}
  • Notă: remarcați că nu este nevoie să interschimbăm variabilele dacă a este inițial mai mic ca b. După prima execuție a buclei while ele se vor interschimba în mod natural.
  • Exercițiu: doi prieteni, un iepure și o broscuță joacă un joc: pornesc de la o linie de start și încep să sară. Broasca sare n centimetri, iar iepurele m centimetri. Cine este mai în spate vine la rînd să sară. Jocul se termină atunci cînd iepurele și broasca sînt iarăși la egalitate. Cîți centimetri au parcurs cei doi prieteni? Răspuns: după cum se vede și din figură, broscuța și iepurele vor sări o lungime egală cu CMMMC(m, n). Precum știm CMMMC(m, n) = m ∙ n / CMMDC(m, n).
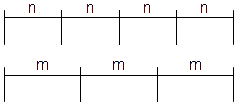
    Săriturile broscuței și iepurelui

Interschimbarea a două variabile (swap)

  • Uneori, în algoritmi, este necesar ca două variabile să își schimbe între ele valorile, astfel încît valoarea care era la început în a să se afle în final în b și valoarea care era la început în b să se afle în a. Această operație se cheamă interschimbare (swap). O metodă naivă și greșită ar fi următoarea:a = b;b = a;Aceasta ar duce la un alt rezultat, și anume ambele variabile ar conține în final vechea valoare a lui b.
  • Pentru a înțelege mai bine soluția vom face o analogie cu o altă problemă: să presupunem că avem două pahare a și b, paharul a plin cu apă și paharul b plin cu lapte. Să presupunem că vrem să schimbăm conținutul paharelor astfel încît paharul a să conțină în final lapte și paharul b să conțină în final apă. Este clar că nu putem rezolva problema fără a ne folosi de un al treilea pahar, gol, să îi spunem aux, de la auxiliar. Pentru a face interschimbul putem vărsa paharul a în paharul aux, apoi paharul b în paharul a și în final paharul aux în paharul b.
  • Similar, pentru a interschimba variabilele a și b vom folosi o a treia variabilă aux:aux = a;a = b;b = aux;
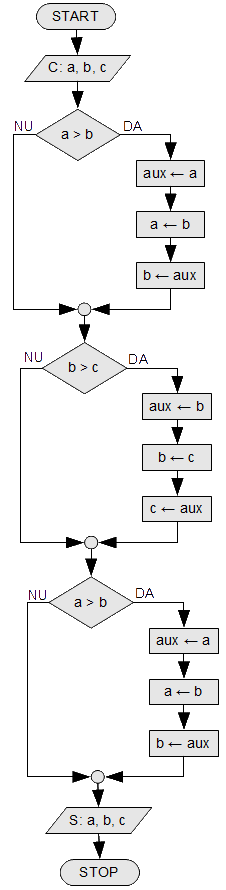
  • Exemplu: sortarea a trei numere, revizitată. Se citesc trei numere a, b și c, să se afișeze în ordine crescătoare. Am făcut deja o schemă logică care rezolvă problema testînd toate variantele. Iată o soluție mai simplă bazată pe interschimbarea variabilelor. Vom proceda de așa natură încît în final a, b și c să fie în ordine. Pentru aceasta vom interschimba două variabile dacă ordinea este greșită. Iată schema logică și programul C:
Sortare prin interschimbare
 
#include <stdio.h>

int main() {
  int a, b, c, aux;

  scanf( "%d%d%d", &a, &b, &c );
  if ( a > b ) {
    aux = a;
    a = b;
    b = aux;
  }
  if ( b > c ) {
    aux = b;
    b = c;
    c = aux;
  }
  if ( a > b ) {
    aux = a;
    a = b;
    b = aux;
  }
  printf( "%d %d %d", a, b, c );

  return 0;
}

Tema

  • Să se rezolve următoarele probleme (schemă logică + program C în CodeBlocks):
    • Pavaj: să se paveze un dreptunghi cu pătrate maximale. Se citesc a și b numere naturale, dimensiunile laturilor dreptunghiului, să se afișeze latura pătratelor cele mai mari cu care putem acoperi dreptunghiul, precum și numărul lor. Exemple: dacă a este 3 și b este 4 vom afișa 1 și 12 (cel mai mare pătrat cu care putem acoperi dreptunghiul are latură 1 și avem nevoie de 12 astfel de pătrate); dacă a este 6 și b este 8 vom afișa 2 și 12; dacă a este 12 și b este 20 vom afișa 4 și 15.
    • Ordonare: se citesc patru numere, a, b, c și d. Să se afișeze în ordine crescătoare. Folosiți interschimbări de variabile.
    • Cifră: se citește un număr n, să se spună dacă este format dintr-o singură cifră, repetată. Exemple: 3333 este un astfel de număr, 2424 nu este, 5 este, 88 este.
  • Problemă de logică: un rege ar fi trebuit să primească zece fișicuri de monede a cîte zece grame fiecare. Din nefericire unul din fișicuri conține zece monede a cîte 9 grame, în loc de zece. Dispunem de un cîntar cu eroare mai mică de un gram și avem voie să facem o singură cîntărire. Cum vom proceda pentru a descoperi fișicul cu monede mai ușoare?

Rezolvări aici [2]

Retrieved from "https://www.algopedia.ro/wiki/index.php?title=Clasa_a_V-a_lecția_10_-_06_nov_2012&oldid=6884"