Clasa a V-a lecția 10 - 26 oct 2019
Tema - rezolvări
Rezolvări aici [1]
Lecție
<html5media height="720" width="1280">http://algopedia.ro/video/2019-2020/2019-10-26-clasa-5-lectie-info-10-720p.mp4</html5media> Comentariu: filmul este incomplet. Camera a fost accidental deconectată de la alimetare.
Fișiere
În general dorim să păstrăm rezultatele calculate de un program, nu doar să le afișăm pe ecran. De asemenea, atunci cînd testăm programul am vrea să nu trebuiască să tastăm datele de intrare la fiecare execuție, mai ales atunci cînd sînt multe. Fișierele sînt un mod de a stoca datele pe disc, fie în vederea citirii lor de către un program, fie pentru a păstra rezultatele.
Declararea fișierelor
FILE *fin, *fout; // un fisier de intrare (citire) si unul de iesire (scriere)Deschiderea și închiderea fișierelor
Pentru a putea citi dintr-un, sau scrie într-un fișier acesta trebuie mai întîi deschis. La final el trebuie închis. Un fișier de intrare (citire) se deschide în modul citire, iar un fișier de ieșire (scriere) se deschide în modul scriere:
fin = fopen( "date-intrare.in", "r" );
... facem citiri din fisier
fclose( fin );
fout = fopen( "rezultate.out", "w" );
... facem scrieri in fisier
fclose( fout );Citirea din și scrierea în fișiere
Instrucțiunea de citire este similară cu scanf. Ea se numește fscanf (scanf din fișier) și are ca prim argument fișierul din care se citește. Exemplu:
fscanf( fin, "%d", &n );Instrucțiunea de scriere este similară cu printf. Ea se numește fprintf (printf în fișier) și are ca prim argument fișierul în care se scrie. Exemplu:
fprintf( fout, "Numărul %d este prim\n", n );Exemplu de lucru cu fișiere
Se citesc două numere m și n. Să se spună dacă sînt prime între ele (dacă nu au nici un divizor mai mare ca 1). Răspuns: am putea să testăm toți divizorii posibili, între 2 și minimul celor două numere, dar ar fi ineficient. Putem în schimb calcula cel mai mare divizor comun, și dacă el este 1 înseamnă că nu există nici un divizor mai mare ca 1, prin definiție.
#include <stdio.h>
int main() {
FILE *fin, *fout;
int a, b, r;
fin = fopen( "prime.in", "r" );
fscanf( fin, "%d%d", &a, &b );
fclose( fin );
while ( b > 0 ) {
r = a % b;
a = b;
b = r;
}
fout = fopen( "prime.out", "w" );
if ( a > 1 )
fprintf( fout, "Nu\n" );
else
fprintf( fout, "Da\n" );
fclose( fout );
return 0;
} |
Radical
Definiție: numim radical din n și scriem acel număr a care ridicat la pătrat este n. Cu alte cuvinte dacă a2 = n atunci a =.
Funcția care calculează radical din n în C se numește sqrt. sqrt(n) calculează radical din n, iar, dacă îl atribuim unei variabile întregi, ea va conține partea întreagă din radical. Cu alte cuvinte variabila va conține cel mai mare întreg a cu proprietatea că a2 ≤ n.
Pentru a putea folosi funcția sqrt va trebui să includem <math.h>.
Exemplu: să se calculeze radical din n și să se afișeze.
#include <stdio.h>
#include <math.h>
int main() {
FILE *fin, *fout;
int n, a;
fin = fopen( "radical.in", "r" );
fscanf( fin, "%d", &n );
fclose( fin );
a = sqrt( n );
fout = fopen( "radical.out", "w" );
fprintf( fout, "%d\n", a );
fclose( fout );
return 0;
} |
Exercițiu
Scrieți schema logică și programul C pentru următoarea problemă, folosind fișiere pentru citirea și scrierea datelor.
Cîte pătrate perfecte sînt între a și b? De exemplu, dacă a = 4 și b = 16 vom răspunde 3, deoarece sînt 3 numere pătrate perfecte între 4 și 16, și anume 4, 9 și 16. Dacă a = 10 și b = 100 vom răspunde 7, deoarece sînt 7 numere pătrate perfecte între 10 și 100, și anume 16, 25, 36, 49, 64, 81 și 100.
Avem mai multe variante de rezolvare.
Rezolvare 1
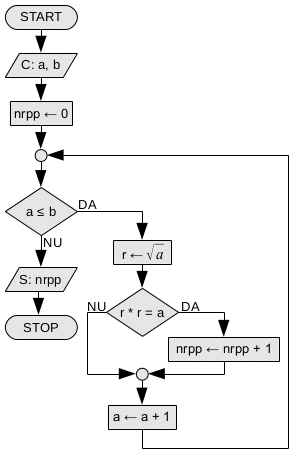
Cea mai simplă metodă ar fi să considerăm toate numerele între a și b și să testăm dacă sînt pătrate perfecte, caz în care vom aduna unu la un contor. Testul de pătrat perfect îl vom face ca în tema 2, problema copiilor ce se pot sau nu așeza în pătrat. Mai precis, vom calcula radicalul numărului de test pe care îl vom ridica la pătrat. Dacă rezultatul este egal cu numărul inițial el este pătrat perfect.
Rezolvare 2
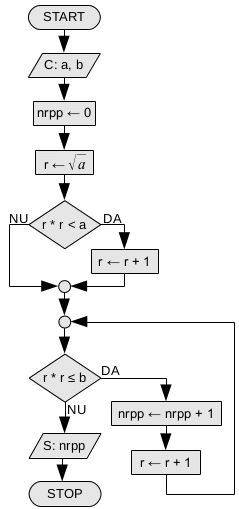
Rezolvarea 1 va testa toate numerele între a și b. O rezolvare ceva mai bună ar lua în considerare doar pătratele perfecte între a și b. Putem porni cu r, radicalul primului pătrat perfect mai mare sau egal cu a. Apoi vom crește r cîtă vreme pătratele generate, r*r, sînt mai mici ca b. La fiecare avans al lui r adunăm unu la contorul de pătrate perfecte. Cum calculăm cel mai mic r cu proprietatea că r*r ≥ a? Vom calcula radicalul lui a în r, iar dacă r*r<a vom mări r cu unu.
Rezolvare 3
Există, oare, o rezolvare mai bună? Desigur! Vom folosi aceeași metodă pe care am folosit-o la rezolvarea problemei divizibilitate în lecția 3, care cerea să se afișeze numărul de numere divizibile cu k în intervalul [a, b].
Vom rezolva mai întîi o problemă mai simplă: să se spună cîte pătrate perfecte există între 1 și x. Acest număr, dacă ne gîndim puțin, este chiar . Dar numărul de pătrate perfecte între a și b? El este numărul de pătrate perfecte între 1 și b, minus numărul de pătrate perfecte între 1 și a-1. Astfel obținem formula:
Iată cea mai eficientă variantă:
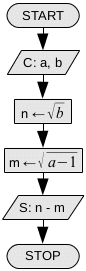 |
Concluzie: matematica este esențială în informatică, ea ducînd la cele mai bune soluții.
Tema
- Faceți-vă cont la varena.ro. După aceea, va trebui sa îmi trimite-ți pe email numele contului vostru să vă caut. Dacă nu îl știu nu voi avea cum sa verific dacă ați urcat problemele și implicit dacă v-ați făcut tema.
- Tema 10: să se rezolve următoarele probleme (schemă logică + program C în CodeBlocks, trimis la vianuarena):
- Problemă de logică: te afli pe o platformă la 200m înălțime. Platforma are un inel bine ancorat. Mai jos, la 100m de pămînt se află o platformă identică. Dispui de o frînghie de 150m și o foarfecă. Cum ajungi la pămînt?
- Rezolvați în CodeBlocks rezolvarea 3 de la lecția curentă. Aceasta trebuie trimisă pe email alături de problema de logică și numele contului vostru.
Rezolvări aici [2]