Clasa a V-a lecția 14 - 13 nov 2013
Tema – rezolvări
Rezolvări aici [1]
Lecție
Exerciții cu secvențe
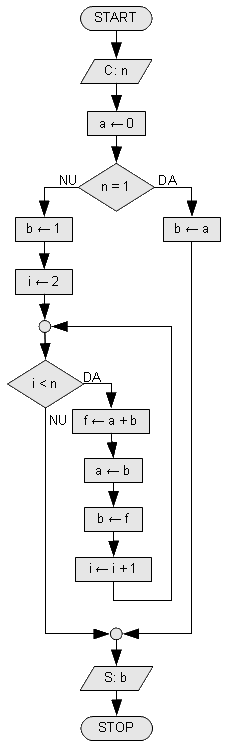
Șirul lui Fibonacci
Definiție: șirul lui Fibonacci este secvența de numere 0, 1, 1, 2, 3, 5, 8, 13... Regula acestei secvențe este că primele două numere sînt 0 și 1, iar următoarele numere sînt suma celor două numere din-naintea lor. Exercițiu: dat n, să se calculeze al n-lea termen din șirul lui Fibonacci.
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, i, a, b, f;
fin = fopen( "fibonacci.in", "r" );
fscanf( fin, "%d", &n );
fclose( fin );
a = 0;
if ( n == 1 )
b = a;
else {
b = 1;
for ( i = 2; i < n; i++ ) {
f = a + b;
a = b;
b = f;
}
}
fout = fopen( "fibonacci.out", "w" );
fprintf( fout, "%d", b );
fclose( fout );
return 0;
}
|
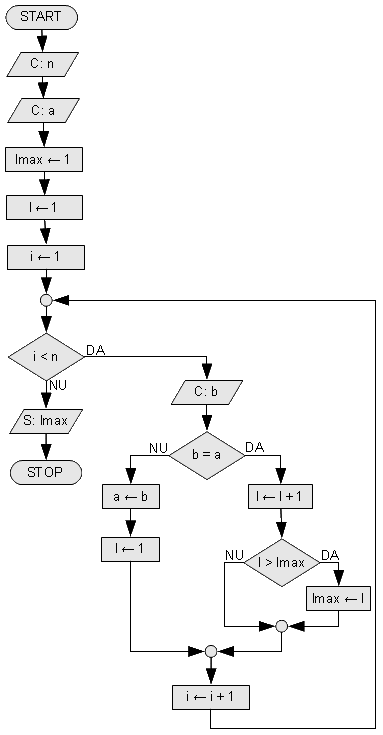
Numere identice
Se dă o secvența de n numere. Să se spună care este numărul maxim de numere identice consecutive în secvență. Exemple:
| identice.in | identice.out | Explicație |
|---|---|---|
| 10 6 2 2 5 8 8 8 2 2 5 |
3 | Numărul 8 apare de trei ori la rînd. Nici un alt număr nu apare de mai multe ori la rînd. |
| 14 8 8 3 3 3 3 1 1 1 5 5 5 5 2 |
4 | Numărul 3 apare de patru ori la rînd. De asemenea și numărul 5 apare de patru ori la rînd. Nici un alt număr nu apare de mai multe ori la rînd. |
Rezolvare:
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, i, a, b, l, lmax;
fin = fopen( "identice.in", "r" );
fscanf( fin, "%d", &n );
fscanf( fin, "%d", &a );
lmax = 1;
l = 1;
for ( i = 1; i < n; i++ ) {
fscanf( fin, "%d", &b );
if ( b == a ) {
l++;
if ( l > lmax )
lmax = l;
} else {
a = b;
l = 1;
}
}
fclose( fin );
fout = fopen( "identice.out", "w" );
fprintf( fout, "%d", lmax );
fclose( fout );
return 0;
}
|
Observații:
- Și aici ținem minte elemetul anterior în secvență, pentru a-l putea compara cu cel actual.
- O alternativă mai eficientă ar fi să comparăm l > lmax numai atunci cînd b ≠ a. Se poate și așa, dar trebuie să avem grijă în cazul în care cea mai lungă secvență este chiar la final. Pentru acest caz particular va trebui ca imediat după bucla WHILE-DO să mai testăm o dată dacă l > lmax.
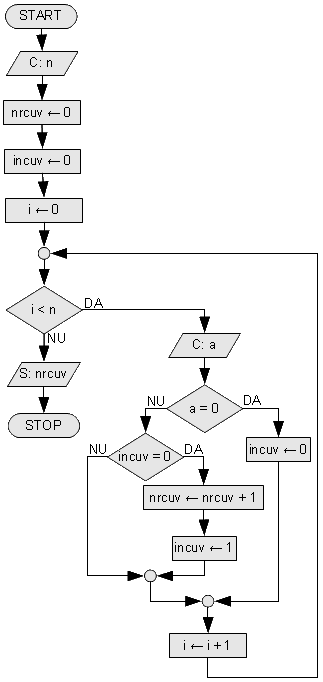
Numărare de cuvinte
Considerăm o secvență de numere. Să considerăm zerourile ca spații, iar numerele diferite de zero ca litere. Dorim să numărăm cîte cuvinte avem în secvență. Exemple:
| cuvinte.in | cuvinte.out | Explicație |
|---|---|---|
| 10 3 5 0 0 2 9 7 0 1 3 |
3 | Sînt trei cuvinte (subsecvenţe de numere diferite de zero), 3 5, 2 9 7 şi 1 3. |
| 10 0 0 0 2 6 1 0 0 1 0 |
2 | Sînt două cuvinte (subsecvenţe de numere diferite de zero), 2 6 1 şi 1. |
O variantă de rezolvare ar fi să ne uităm la două numere consecutive în secvență și să vedem dacă începe un cuvînt (sau dacă se termină). O a doua variantă este să ținem o variabila incuv care să ne spună dacă ne aflăm în interiorul unui cuvînt sau nu. Vom prefera această variantă deoarece este mai simplă și se poate generaliza pentru situații mai complicate.
 |
#include <stdio.h>
int main() {
FILE *fin, *fout;
int n, i, a, incuv, nrcuv;
fin = fopen( "cuvinte.in", "r" );
fscanf( fin, "%d", &n );
nrcuv = 0;
incuv = 0;
for ( i = 0; i < n; i++ ) {
fscanf( fin, "%d", &a );
if ( a == 0 )
incuv = 0;
else
if ( incuv == 0 ) {
nrcuv++;
incuv = 1;
}
}
fclose( fin );
fout = fopen( "cuvinte.out", "w" );
fprintf( fout, "%d", nrcuv );
fclose( fout );
return 0;
}
|
Temă
- Rezolvați problema concurs dată la OJI 2004 (schemă logică + program C).
- Rezolvați problema subsecvență crescătoare (schemă logică + program C).
- Problemă de logică: zece oameni sînt așezați în șir, unul în spatele altuia. Li se așează pe cap cîte o tichie neagră sau albă. Fiecare om poate să vadă tichiile oamenilor din fața lui. Începînd cu ultimul, cel mai din spate, oamenii strigă pe rînd "alb" sau "negru". După ce strigă, ei sînt scoși din rînd și duși într-o cameră unde sînt eliberați, dacă și-au ghicit culoarea tichiei, sau omorîți în caz contrar. Un om poate să audă ce au strigat, pe rînd oamenii din spatele său. Oamenii nu au voie să comunice în nici un alt fel, cum ar fi să tușească, să se atingă, etc, sau vor fi omorîți toți! Ei au voie să se sfătuiască înainte să fie așezați, pentru a stabili strategia prin care să salveze cîți mai mulți dintre ei. Voi trebuie să stabiliți ce strategie aleg oamenii și care este numărul maxim de oameni pe care îi puteți salva. Exemplu: să presupunem că oamenii aleg următoarea strategie: ei vor striga, pe rînd, "alb", cu toții. În acest caz vor supraviețui 5 oameni, pe medie.
Rezolvări aici [2]
