Clasa a V-a lecția 32 - 14 mar 2020
Anunțuri
- Felicitări tuturor participanților și în special celor care au obținut punctajul minim de calificare pentru ONI!
- Toți cei care s-au calificat la etapa Națională și au trecut la profesorii îndrumători unul dintre profesorii Nerdvana vor beneficia de cursurile cercului IQ Academy gratuit, până la susținerea Olimpiadei Naționale de Informatică.
- Toți elevii care vor participa la Olimpiada Națională de Informatică, vor avea menționați profesori Nerdvana ca profesori îndrumători și vor obține medalia de aur vor beneficia gratuit de cursurile IQ Academy, pe durata anului 2020 - 2021.
- Rezultatele olimpiadei județene de informatică ale studenților IQ Academy:
| Nr.Crt. | Nume | Prenume | Prof indrumator | P1 | P2 | Total | Status |
|---|---|---|---|---|---|---|---|
| 1 | GAVRIȘ | MIHAI VLADIMIR | BOCA ALINA GABRIELA, MIHAI TUTU | 97 | 88 | 185 | Clasament National (CN) |
| 2 | GRAMA | ANDREI TEODOR | ALINA-GABRIELA BOCA, ANCA KNOPF , MIHAI TUȚU | 100 | 79 | 179 | Clasament National (CN) |
| 3 | COMAN | ANDREI | ALINA-GABRIELA BOCA, ANCA KNOPF , MIHAI TUTU , ALEXANDRU MIHAI OPREA | 100 | 70 | 170 | Clasament National (CN) |
| 4 | POTERAȘU | DAVID | ALI CABAS, GEANAU ADRIANA | 70 | 55 | 125 | Clasament National (CN) |
| 5 | BOABEȘ | CRISTINA | KISCH MARIANA | 61 | 58 | 119 | Clasament National (CN) |
| 6 | ZAMFIR | LUCA-CRISTIAN | ALINA- GABRIELA BOCA, MIHAI TUȚU | 40 | 74 | 114 | Clasament National (CN) |
| 7 | BĂDOIU | DARIA ȘTEFANIA | DINU ANDREEA | 40 | 38 | 78 | Punctaj insuficient (P) |
| 8 | MISCOCI | VLAD | MIHAI TUTU , ALI CABAS | 10 | 10 | 20 | Punctaj insuficient (P) |
| 9 | VASILE | BRIANA | TELE MONICA, TUTU MIHAI, CABAS ALI | 10 | 10 | 20 | Punctaj insuficient (P) |
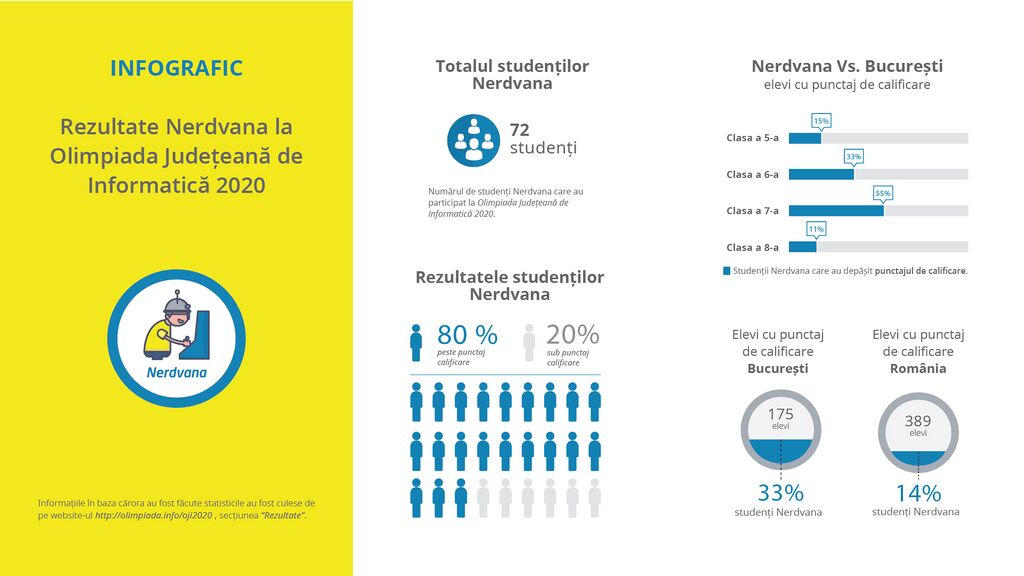
Statistici Nerdvana
Lecție - rezolvarea problemelor de la OJI 2020
<html5media height="720" width="1280">http://algopedia.ro/video/2019-2020/2020-03-14-clasa-5-lectie-info-32-720p.mp4</html5media>
Lecția video cuprinde doar prima ora. Cea de-a doua oră a fost aplicativă și s-a discutat problema minute.
Problema cartonașe
Problema cartonașe este una mai degrabă banală pentru că am rezolvat ceva foarte asemănător, chiar la începutul lecțiilor despre secvență. Mă refer la problema subcresc.
Este o problemă de numărare, după regulile date de problemă. Nu are o rezolvare specială, pentru că nu este o problemă de matematică, nu are vreun șiretlic și nici nu necesită dopaj.
Iată o posibilă rezolvare:
#include <stdio.h>
#include <stdlib.h>
int main()
{
FILE *fin, *fout;
int cerinta, numar_linii, linie, cartonas1, cartonas2, un_capat, perechi,secventa , secventa_maxima, numar_secvente_maxime;
fin = fopen ("cartonase.in", "r");
fscanf (fin, "%d%d%d", &cerinta, &numar_linii, &un_capat); // citim totodată primul capăt al cartonașului, întrucât nu îl vom folosi la nimic
perechi = 0;
secventa = secventa_maxima = numar_secvente_maxime = 1;
for (linie = 0; linie < numar_linii; linie++) {
fscanf (fin, "%d%d", &cartonas1, &cartonas2); // citim sfârșsitul primului cartonaș și începutul celui de-al doilea
if(cartonas1==cartonas2) { // dacă aceste două capete sunt egale
perechi++; // numărăm perechile pentru cerința 1
secventa++; // numărăm lungimea secvenței actuale
} else { // dacă nu sunt cartonașe la fel
if (secventa > secventa_maxima) { // verificăm dacă este cea mai lungă secvență
secventa_maxima = secventa; // dacaă da, o reținem
numar_secvente_maxime = 1; // resetăm numărul de secvențe maxime pentru că am găsit o nouă secvență maximă
} else {
if (secventa == secventa_maxima) { // dacă secvența este la fel de mare
numar_secvente_maxime++; // adăugăm la contor numărul de apariții
}
}
secventa=1; // resetăm secvența la un cartonaș, cea mai mică secvență
}
}
fclose(fin);
fout = fopen ("cartonase.out", "w");
if (cerinta == 1) {
fprintf(fout, "%d", perechi);
} else if (cerinta == 2) {
fprintf(fout, "%d", secventa_maxima);
} else {
fprintf(fout, "%d", numar_secvente_maxime);
}
fclose(fout);
return 0;
}Problema tai
Problema tai este o problemă pe care colegii voștri o numesc "problemă tractor". Adică este o problemă la care scrii mult, repetitiv și pentru un rezultat care, în opinia mea, nu aduce un plus valoare cunoștințelor voastre. Mai mult, soluția comisiei propune folosirea funcțiilor, care nu se află în materia pentru clasa a 5-a.
Rezolvarea problemei se învârte în verificarea unui număr dacă este prim. Vom folosi metoda pe care am învățat-o la începutul cercului cu problema număr prim. Vom căuta divizorii eficient, până la radicalul numărului. Dacă întâlnim un divizor, ne oprim, pentru că nu mai are sens să continuăm, numărul nu este prim.
divizor = 2;
while (numar % divizor !=0 && divizor * divizor <= numar)
divizor++;
if (divizor * divizor > numar) {
if (numar > prim_maxim)
prim_maxim = numar;
}Vom repeta acest cod de 6 ori pe parcursul problemei:
- O singură dată pentru prima cerință;
- De două ori pentru cerința a doua;
- De trei ori pentru a treia cerință.
Sună bine, nu?
Cerința 1 presupune să aplicăm algoritmul de mai sus pe fiecare număr citit. Deci, citim numărul și apoi verificăm dacă este prim. Dacă este prim, verificăm dacă este cel mai mare număr prim.
Cerința 2 complică doar puțin lucrurile. Trebuie să facem o tăiere și să obținem două numere dintr-unul. Vom avea nevoie de o variabilă putere a lui 10, p10_cerinta2, pentru a putea forma numerele. Vom folosi operația mod p10_cerinta2 pentru a determina primul număr și div p10_cerinta2 pentru a determina cel de-al doilea număr. Apoi vom aplica pentru fiecare dintre cele două numere algoritmul de la prima cerință.
Cerința 3 ne complică programul pentru că trebuie să facem două tăieri. În prima fază, vom face o singură tăiere și vom obține două numere. Apoi, luăm al doilea număr și începem să facem altă tăiere, adică să aplicăm algoritmul de la cerința 2. După ce am generat toate numerele prin tăierea celui de-al doilea număr, revenim la numărul inițial și facem o altă primă tăiere. Repetăm procesul până când obținem toate variantele de numere.
După cum puteți observa, cerința 3 nu aduce plus valoare didactică problemei. Puteam la fel de bine să ne oprim la a doua cerință. Dificultatea reală consta în atenția fiecăruia, pe care comisia s-a bazat că nu o veți avea. Pentru mulți dintre voi, au avut dreptate.
Iată o posibilă rezolvare:
#include <stdio.h>
#include <stdlib.h>
int main()
{
FILE *fin, *fout;
int cerinta, numar_linii, linie, numar, divizor, prim_maxim = 0, p10_cerinta2, p10_cerinta3, numar1, numar2, numar3, copie_numar;
fin = fopen ("tai.in", "r");
fscanf (fin, "%d%d", &cerinta, &numar_linii);
for (linie = 0; linie < numar_linii; linie++) {
fscanf (fin, "%d", &numar);
if (cerinta == 1) { //cerinta 1
divizor = 2;
while (numar % divizor !=0 && divizor * divizor <= numar)
divizor++;
if (divizor * divizor > numar) {
if (numar > prim_maxim)
prim_maxim = numar;
}
} else if (cerinta == 2) { //cerinta 2
p10_cerinta2 = 10;
numar2 = numar; // punem condiția ca numar2 să aibe cel puțin o cifră. Acesta este numărul care se obține prin operația div
while (numar2 > 10) {
numar1 = numar % p10_cerinta2; // obținem primul dintre cele două numere
divizor = 2;
while (numar1 % divizor !=0 && divizor * divizor <= numar1)
divizor++;
if (divizor * divizor > numar1) {
if (numar1 > prim_maxim)
prim_maxim = numar1;
}
numar2 = numar / p10_cerinta2; // obținem al doilea dintre cele două numere
divizor = 2;
while (numar2 % divizor !=0 && divizor * divizor <= numar2)
divizor++;
if (divizor * divizor > numar2) {
if (numar2 > prim_maxim)
prim_maxim = numar2;
}
p10_cerinta2 *= 10;
}
} else { //cerinta 3
p10_cerinta2 = 10; // puterea lui 10 necesară obținerii numărului numar1
p10_cerinta3 = 10; // puterea lui 10 necesară obținerii numărelor numar2 și numar3
numar2 = numar ;
while (numar2 > 10) {
numar1 = numar % p10_cerinta2; // va fi numărul care se va obține mereu din prima tăiere
// el va fi calculat doar după ce se realizează toate celelalte combinații
divizor = 2;
while (numar1 % divizor !=0 && divizor * divizor <= numar1)
divizor++;
if (divizor * divizor > numar1) {
if (numar1 > prim_maxim)
prim_maxim = numar1;
}
copie_numar = numar / p10_cerinta2; // este exact codul de la cerința 2, adaptat la numărul 2 obținut
numar3 = numar2; // în loc să calculăm numar1 și numar2, vom calcula numar2 și numar3 pornind de la numarul obtinut dupa prima taiere
while (numar3 > 10) {
numar2 = copie_numar % p10_cerinta3;
divizor = 2;
while (numar2 % divizor !=0 && divizor * divizor <= numar2)
divizor++;
if (divizor * divizor > numar2) {
if (numar2 > prim_maxim)
prim_maxim = numar2;
}
numar3 = copie_numar / p10_cerinta3;
divizor = 2;
while (numar3 % divizor !=0 && divizor * divizor <= numar3)
divizor++;
if (divizor * divizor > numar3) {
if (numar3 > prim_maxim)
prim_maxim = numar3;
}
p10_cerinta3 *= 10;
}
p10_cerinta2 *= 10;
p10_cerinta3 = 10;
}
}
}
fclose(fin);
if(prim_maxim == 1) {
prim_maxim = 0;
}
fout = fopen ("tai.out", "w");
fprintf(fout, "%d", prim_maxim);
fclose(fout);
return 0;
}Problemă suplimentară - problema minute
Problema minute este din nou un exercițiu de lucrul cu timpul. De asemenea este o problemă de simulare, deoarece trebuie să simulăm funcționarea unui ceas defect. Voi prezenta două soluții la această problemă.
Soluția dată coincide cu cea dată de comisia de olimpiadă. În primul rînd vom face conversia de la ore și minute la minute, pentru a afla cîte minute avem. Apoi vom avansa o variabilă din minut în minut de la zero pînă la numărul total de minute din simulare. În același timp vom avansa ora și minutul ceasului în mod corespunzător:
- Dacă limbile nu sînt suprapuse vom avansa ceasul cu unu. Avansul ceasului se face adunînd unu la minut. Cînd minutul devine 60 el va fi resetat la zero, iar ora va fi incrementată. Cînd și ora devine 12, ea va trebui resetată la 0.
- Dacă limbile se suprapun avem două variante: fie folosim o altă variabilă pentru a ne asigura că următoarele 5 bucle nu avansăm ceasul. Fie, mai simplu, avansăm numărul de minute reale cu 5.
Vă rămîne vouă să vă dați seama care este testul care ne spune dacă cele două limbi sînt suprapuse.
Iată rezolvarea bazată pe ideile expuse în prima soluție:
#include <stdio.h>
int main() {
FILE *fin, *fout;
int h1, m1, h2, m2, mtot;
fin = fopen( "minute.in", "r" );
fscanf( fin, "%d%d%d%d", &h1, &m1, &h2, &m2 );
fclose( fin );
mtot =m2 + 60 * h2; // timpul care trebuie sa mai treaca pina la final
if ( h1 == 12 ) // normalizam ora, de la zero in loc de de la 12
h1 = 0;
while ( mtot > 0 ) { // cita vreme mai avem timp de executat
if ( 5 * h1 == m1 ) { // daca limbile se suprapun - de ex.: ora 3 este echivalentul cu minutul 15, de aici 5 * h1
mtot -= 6; // avansam timpul cu sase minute
if ( mtot >= 0 ) // daca mai avem timp avansam minutarul cu unu
m1++;
} else { // daca limbile nu se suprapun
mtot--; // a mai trecut un minut
m1++; // avansam minutarul
}
if ( m1 == 60 ) { // daca minutarul a ajuns la 60
h1 = (h1 + 1) % 12; // adunam unu la ora, daca e 12 o resetam la 0
m1 = 0; // punem minutarul pe 0
}
}
if ( h1 == 0 ) // renormalizam ora, sa arate 12 daca este 0
h1 = 12;
fout = fopen( "minute.out", "w" );
fprintf( fout, "%d %d\n", h1, m1 );
fclose( fout );
return 0;
}Temă
Tema 32: să se rezolve următoarele probleme (program C trimis la vianuarena):
Rezolvări aici [1]