Clasa a V-a lecția 40 - 10 mai 2018
Tema - comentarii
Comentariu general pentru vizitatori, cei ce nu au mai venit la noi: temele trebuie trimise în cadrul concursului temă, nu la arhivă. Atenție mare! Tot pentru cei noi: citiți vă rog regulamentul. Noi nu folosim freopen. Sursele noastre sînt C, fără elemente aiurea de C++. Ele trebuie să aibă extensia .C Dacă nu vă descurcați scrieți-mi. Setați vă rog opțiunile de compilare, conform celor descrise în pagina principală a cursului, pe algopedia. Apoi uitați-vă la avertismentele de la build. Nu dați ‘build&run’ căci ele dispar. Unii din voi aveți avertismente de variabile neinițializate.
Problema bitonă
- Topul pescarilor la bitonă: Mușat care răspunde mereu ‘DA’ (este un yes-man!), Petcu, care a trimis neînfricată 8 surse (na, penalizărilor, luați palme de aici!), la fel și Asgari, 8 surse, fără teamă de penalizări căci el a trimis surse la arhivă (dar care primește premiul de onoare deoarece nu a copiat o sursă ce ar fi luat 100p deși avea acces la sursele din arhivă), Iordache, 5 surse (care a reușit performanța ca la ultima sursă să ia mai puțin decît la prima)
- Unii dintre voi nu ați înțeles ce înseamnă o secvență bitonă, deși enunțul este clar. De exemplu, o secvență descrescătoare este bitonă.
- Mulți dintre voi ați citit direct primele două elemente ale secvenței, fără să întrebați dacă nu cumva ‘n’ este unu.
- La bitonă unii din voi nu ați folosit exemplul de la lecție. Nu ați fost atenți și v-a ieșit un cod monstruos.
- La bitonă unii din voi au citit toate elementele secvenței de la intrare, nu v-ați oprit cînd v-ați dat seama că nu mai poate fi făcută bitonă.
- La bitonă unii din voi ați calculat creșteri și descreșteri. Aceasta vă complică codul. Creșterile și descreșterile sînt legate una de alta, pot diferi prin cel mult unu. Era suficient să calculați numărul de variații, sau, totuna, numărul de segmente. Era clar, apoi, că segmentele ar fi fost alternative, crescătoare și descrescătoare.
- La bitonă unii din voi ați căutat primul element din secvență diferit de primul într-un mod complet neelegant: ați început mai întîi bucla de citire și testare a secvenței, apoi, în buclă, v-ați întrebat dacă i este unu și, în interiorul buclei, ați pornit bucla de căutare. Trebuia, desigur, să căutați elementul diferit în afara buclei, la început, înainte de a porni bucla principală. Voicu, Burac, Nicola. Alții nici nu v-ați pus problema egalității, ați considerat că dacă primul element din secvență este mai mic sau egal decît al doilea ele sînt în ordine crescătoare. Ceea ce este fals, ele pot fi egale și apoi să urmeze un număr mai mic, ceea ce a dus la programe incorecte.
Tema - rezolvări
Rezolvări aici [1]
Lecţie
<html5media height="720" width="1280">https://www.algopedia.ro/video/2017-2018/2018-05-10-lectie-info-40-720p.mp4</html5media>
Conversii implicite şi conversii explicite
Atunci cînd atribuim unei variabile de un tip o valoare de alt tip programul execută o conversie implicită, aşa cum am văzut mai sus. Putem, însă, să dăm şi comenzi explicite de conversie. Să luăm un exemplu. Iată un calcul incorect:
int a, b;
long long s;
...
s = a + b;Acest program nu funcţionează corect dacă a şi b sînt foarte mari, deoarece adunarea se va face pe numere întregi, abia apoi făcîndu-se conversie la tipul long long. Pentru a forţa conversia implicită la tipul long long putem să facem operaţia de adunare pe rînd:
int a, b;
long long s;
...
s = a;
s = s + b;dar programul se lungeşte şi devine mai puţin citibil. Al doilea mod este prin conversie explicită, astfel:
int a, b;
long long s;
...
s = ((long long)a) + b;Deoarece unul din operanzi este de tip long long, de data aceasta adunarea se va face pe tipul long long, efectuîndu-se corect.
Ce observăm? Conversiile explicite se fac punînd tipul la care dorim să convertim valoarea între paranteze.
Instrucțiunea do-while
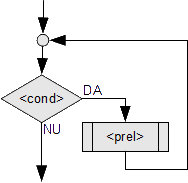
Instrucțiunea do-while în limbajul C implementează o structură repetitivă de tip REPEAT-UNTIL, care este o structură similară cu WHILE-DO. Iată schemele logice pentru cele două structuri alternative:
 |
while ( <cond> ) {
<prel>;
}
|
 |
do {
<prel>;
} while ( !<cond> );
|
Structura REPEAT-UNTIL repetă o secvenţă pînă cînd condiţia este adevărată. De aceea ieşirea din buclă se face pe "DA". Prin contrast, instrucţiunea do-while din C execută corpul buclei cîtă vreme condiţia este adevărată, de unde şi operatorul not (!) introdus în C.
Oricare din cele două structuri repetitive sînt suficiente pentru a descrie orice algoritm. Cu toate acestea, structura WHILE-DO este mai generală decît structura DO-UNTIL, deoarece corpul buclei REPEAT-UNTIL se execută cel puţin o dată, pe cînd bucla WHILE-DO poate să nu se execute nici o dată. Acesta este şi motivul pentru care nu am predat-o pînă acum.
Exemplu
Dîndu-se un număr n să se descompună în sumă de două pătrate perfecte nenule. Vom folosi următoarea metodă: vom căuta o descompunere n = a * a + b * b. Putem considera că a < b, fără a pierde din soluţii. Astfel, vom varia a * a de la 1 pînă la n / 2, verificînd dacă n - a * a este pătrat perfect. Această verificare se face extrăgînd radicalul şi verificînd că pătratul acestuia este chiar numărul original. Iată două variante de implementare, prima folosind while-do, iar a doua folosind do-while:
| Implementare cu WHILE-DO | Implementare cu REPEAT-UNTIL |
|---|---|
a = 1;
d = n - a * a;
b = sqrt( d );
while ( b * b < d && 2 * a * a < n ) {
a++;
d = n - a * a;
b = sqrt( d );
} |
a = 0;
do {
a++;
d = n - a * a;
b = sqrt( d );
} while ( b * b < d && 2 * a * a < n ); |
Se observă că varianta cu do-while este ceva mai scurtă, deoarece nu repetă instrucţiunile care calculează valoarea lui b. Aceste cazuri, în care do-while este preferabilă lui while-do apar mai rar în practică.
Idei pentru jocul Gold
Discuție despre metode de calcul a mutării în jocul Gold.
Mutare de cîștig
Este cea mai ușoară dintre mutări. Dacă observăm că piesa gold este prima din stînga, o ridicăm de pe tablă.
Tablă particulară: o piesă în fața piesei gold
Să ne închipuim o tablă simplificată:
---O---X---
Mai exact, pe tablă sînt doar două piese, din care prima este O și a doua este X. Putem stabili o strategie de cîștig, în acest caz?
Ce-ar fi să mutăm piesa X astfel încît să o "lipim" de piesa O? Cum se va desfășura jocul în acest caz? Mutarea noastră ar fi:
---O---X--- ---OX------
Tablă particulară: două piese în fața piesei gold
Să ne închipuim o altă tablă simplificată:
-O---O--X---
Acum pe tablă sînt fix trei piese, primele două de tip O și ultima piesa gold. Putem stabili o strategie de cîștig?
Ce-ar fi să luăm în considerare două distanțe: cea dintre prima piesă și margine (numărul de căsuțe goale), să-i spunem d0, și cea dintre X și piesa din fața lui, să-i spunem d1. Am putea să mutăm astfel încît să menținem aceste distanțe egale. Dacă d0 este mai mare, vom muta prima piesă O. Dacă d1 este mai mare, vom muta chiar piesa X. Cum se va desfășura jocul în acest caz? Mutarea noastră ar fi, pe tabla anterioară:
-O---O--X--- -O---O-X----
Numărul pipx
Numărul pip provine, la origine, din jocul de table. El ne arată cîte mutări atomice (de o căsuță) putem face în total, cu toate piesele.
În cazul jocului Gold ar fi util să știm numărul maxim de mutări pe care îl putem face cu piesele din dreapta piesei X. De exemplu, să considerăm tabla:
-O-O--X---O--O-OO--
Avem patru piese O după piesa X. Putem muta piesele O, fără a muta piesa X, pînă ce ajungem în poziția
-O-O--XOOOO--------
Cîte mutări de o căsuță putem face?
- prima piesă va muta peste 3 spații
- a doua piesă va muta peste 5 spații
- a treia piesă va muta peste 6 spații
- a patra piesă va muta tot peste 6 spații
Numărul pipx va fi suma acestor numere, respectiv 20.
Cum variază numărul pipx? Avem trei variante:
- Mutare a unei piese de la stînga lui X. În acest caz este simplu, pipx nu se modifică.
- Mutare a unei piese de la dreapta lui X cu C căsuțe. În acest caz pipx scade cu numărul de căsuțe mutate, pipx = pipx - C;
- Mutare a piesei X cu C căsuțe. În acest caz pipx-ul fiecărei piese O de după X crește cu C, deci pipx va crește cu C · NP, unde NP este numărul de piese O de la dreapta lui X: pipx = pipx + C * NP;
Le ce ne este util numărul pipx? Să discutăm, mai jos.
Combinarea lui pipx cu cele două table particulare
Să presupunem că avem o singură piesă în fața piesei gold, dar, de data aceasta, avem și piese dincolo de gold. Avem o strategie de cîștig dacă nu avem piese dincolo de gold. Dar în acest caz putem face ceva?
În cazul în care nu avem piese după gold știm care sînt configurațiile cîștigătoare. Dar acum putem muta și piese după gold. Deci, pare că o poziție cîștigătoare a tablei ar fi una în care dacă adversarul încearcă să "tragă de timp" mutînd o piesă la dreapta piesei gold, să putem și noi trage de timp în același fel.
O idee ar fi să încercăm să mutăm astfel încît pipx să fie par. Dar dacă acest lucru nu se poate? Atunci putem încerca să lăsăm o configurație pierzătoare pentru noi pe tablă, dar să mutăm ceva astfel încît pipx să fie impar.
Scopul final este:
- Fie să lăsăm o configurație cîștigătoare pentru noi pînă la X și pipx par
- Fie să lăsăm o configurație cîștigătoare pentru adversar pînă la X și pipx impar
Pentru aceasta putem acționa asupra pieselor din stînga lui X dacă nu vrem să influențăm pipx. Putem acționa asupra pieselor din dreapta lui X pentru a influența paritatea lui pipx. Sau, mai drastic, putem acționa asupra piesei X, lucru care va influența atît poziția de cîștig cît și paritatea lui pipx.
Exemplul 1: mutare piesă la stînga piesei gold
În acest exemplu pipx este 24, deci par:
---O-O--X-O--O--O-O---O- --O--O--X-O--O--O-O---O-
Mutînd prima piesă am lăsat pe tablă o poziție cîștigătoare în stînga lui X și nu am influențat pipx, deci el a rămas par. Sîntem, deci, într-o situație favorabilă.
Exemplul 2: mutare piesă la dreapta piesei gold
În același exemplu, pipx este 24, deci par.
---O-O--X-O--O--O-O---O- ---O-O--X-O--O--OO----O-
Am mutat penultima piesă o poziție la stînga, ceea ce va scădea pipx' cu unu, el devenind impar. Am lăsat, deci o poziție pierzătoare pe tablă (pierzătoare pentru noi), dar cu pipx impar. Sîntem, deci, într-o situație favorabilă.
Exemplul 3: mutare piesă gold
Același exemplu, pipx este 24, deci par.
---O-O--X-O--O--O-O---O- ---O-O-X--O--O--O-O---O-
Am mutat piesa X o poziție la stînga. În acest caz pipx crește cu 5, ceea ce înseamnă că paritatea se schimbă. Poziția de la stînga lui X este pierzătoare, dar și paritatea lui pipx este impară, deci sîntem într-o situație favorabilă.
Voi lăsa lucrurile aici, deoarece nu este clar cum să mutăm, chiar și cunoscînd aceste lucruri.
Atenție:
- Nu este obligatoriu să avem mutare perfectă, urmărind aceste reguli
- Chiar și dacă reușim să mutăm "bine", este posibil ca în viitor să ajungem iar la o poziție nefavorabilă și să trebuiască să reechilibrăm
În concluzie pipx este o armă, dar nu una infailibilă.
Mutare aleatoare
Deși poate suna ciudat, atunci cînd nu avem nici o idee de mutare, putem muta aleator, sau la întîmplare (în engleză random). Ce înseamnă acest lucru? Că vom selecta o piesă de pe tablă, la întîmplare, și o vom muta. O putem muta cu o căsuță la stînga (dacă se poate), sau chiar mai multe.
Cum putem face acest lucru?
Presupunînd că avem numărul pieselor, NP, avem nevoie să putem genera un număr la întîmplare între 1 și NP pentru a alege piesa de mutat. Sau și mai bine, cum ne place nouă informaticienilor, avem nevoie de un număr între 0 și NP-1 :-) Pentru aceasta am putea să ne legăm de valori ale unor variabile din program. De exemplu, am putea să luăm valorile tuturor elementelor vectorului care memorează tabla de joc și să le înmulțim. Apoi vom calcula rezultatul modulo NP, rezultînd un număr între 0 și NP-1.
Aceasta este o soluție foarte bună la nivel de clasa a cincea. Dacă vreți să încercați și altceva, limbajul C ne pune la dispoziție un mod de a genera numere aleatoare. Iată, mai jos, un exemplu:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main() {
int poz, np;
// ... declaratii alte variabile
srand ( time( NULL ) ); // initializare a generatorului de numere aleatoare
// ... instructiuni
poz = rand() % np; // genereaza un numar aleator intre 0 si np-1 (0 ≤ poz < np)
// ... instructiuni
}Observații:
- Pentru a folosi
rand()trebuie să includețistdlib.h. - Pentru a folosi
srand( time( NULL ) )trebuie să includețitime.h. - Apelați
srand( time( NULL ) )o singură dată, înainte de prima folosire a luirand(). - Apelați
rand()ori de cîte ori aveți nevoie în programul vostru, pentru a genera un nou număr aleator.
Temă
Lucrați la jocul Gold. Cei ce vor să participe dar nu mi-ați dat încă email, sau mi-ați dat email dar nu vă vedeți înscriși în tabelul concurenților, dați-mi vă rog email să mă anunțați că participați.