Clasa a V-a lecția 6 S12
Structura repetitiva DO WHILE
Structura repetitivă de tip DO-WHILE (execută -cîtă timp) reprezinta structura de control cu ajutorul careia executam un set de instructiuni, de mai multe ori, in functie de o conditie. Spre deosebire de instructiunea WHILE –DO, aceasta structura executa mai intai blocul de instructiuni si mai apoi testeaza conditia.

Mecanism:
Pasul 1. Se executa pachetul de instructiuni “Prel”; Pasul 2: Se testeaza conditia. Daca conditia este adevarata atunci revenim la pasul 1. Daca conditia este falsa se trece la pasul 3. Pasul 3. Stop
Obs: Spre deosebire de instructiunea while-do, instructiunea do –while, executa cel putin odata pachetul de instructiuni, indiferent de valoarea de adevar a expresiei logice(conditie). Orice instructiune do-while, poate fi inlocuita de o instructiunea while, echivalenta (vezi tabelul).
Aplicatii
Suma cifrelor unui numar
Sã se realizeze un algoritm ce calculeazã suma cifrelor unui numar natural.
| Pseudocod | C | C++ |
|---|---|---|
citeste n; s ← 0; Repeta s ← s + n%10 n ← n/10 cat-timp (n>0) scrie s |
#include<stdio.h>
int main(){
int n,s;
scanf(“%d”,&n);
s=0;
do{
s=s+n%10;
n=n/10;
}while(n>0);
printf(“%d”,s);
return 0;
} |
#include <iostream>
using namespace std;
int main(){
int n,s; cin>>n;
s=0;
do{
s=s+n%10;
n=n/10;
}while(n>0);
cout<<s;
return 0;
} |
Cifra de control
Se citeste un numar n. Afisati cifra de control a numarul n. Cifra de control se obtine prin adunarea repetata a cifrelor numarului pana cand se obtine o singuracifra. Ex: n=193 s=1+9+3=13 s=1+3=4
#include <iostream>
using namespace std;
int main(){
int n, s;
cout << "Dati un numar n:" << endl;
cin >> n;
do{
s = 0;
while( n > 0 ){
s = s + n % 10;
n = n / 10;
}
n = s;
}while( s > 9 );
cout << "Cifra de control este " << s;
return 0;
}O alta metoda de rezolvare: cifcontrol = ( n-1 ) % 9 + 1
Descompunerea in factori primi
Varianta1 cu do while
Vom imparti numarul repetat la factori primi, pana cand acesta devine 1. Atentie la afisare: Cand afisam primul factor nu vom mai pune "*" inainte.
#include<stdio.h>
int main(){
int n, p, d, pas;
scanf( "%d", &n );
d = 2; pas = 1;
do{
p = 0; ///impartim pe n la d de cate ori se poate
while( n % d == 0 ){
n= n / d;
p = p + 1; ///rezulta p, ca fiind puterea divizorului
}
if( p > 0 )
if( pas == 1 ){
printf("%d^%d", d, p);
pas = pas + 1;
}
else
printf("*%d^%d", d, p);
d = d + 1;
}while( n > 1 ); ///cata vreme n nu a fost descompus
return 0;
}Varianta 2 cu while do
Atentie la afisare: Cand vom afisa ultimul factor nu vom mai pune "*" dupa.
#include <stdio.h>
int main(){
int n, d, p;
scanf( "%d", &n ); // cin>>n;
d = 2;
while(n > 1){
p = 0;
while( n % d == 0 ){
n = n / d;
p = p + 1;
}
if(p != 0)
if(n == 1) //ca am gasit un ultim factor
printf("%d^%d", d, p); //cout<<d<<"^"<<p;
else
printf("%d^%d*", d, p); //cout<<d<<"^"<<p<<"*";
d = d + 1;
}
return 0;
}Varianta2 cu do-while
#include <stdio.h>
int main(){
int n, d, p;
scanf("%d",&n); //cin>>n;
d = 2;
do{
p = 0;
while( n % d == 0 ){
n = n / d;
p = p + 1;
}
if(p != 0)
if(n == 1) //ca am gasit un ultim factor
printf("%d^%d", d, p); //cout<<d<<"^"<<p;
else
printf("%d^%d*", d, p); //cout<<d<<"^"<<p<<"*";
d = d + 1;
}while(n != 1);
return 0;
}Descompunere in factori primi - Optimizare
#include <stdio.h>
int main(){
int n, d, p;
scanf( "%d", &n );
d = 2;
while(d * d <= n){
p = 0;
while(n % d == 0 ){
n = n / d;
p = p + 1;
}
if( p > 0 )
printf("%d %d\n", d, p);
d = d + 1;
}
// verificam daca mi-a mai ramas in n un factor prim
if ( n > 1)
printf("%d 1", n);
return 0;
}Algoritmul lui Euclid - cmmdc
Algoritmul lui Euclid este o metodă eficientă de calcul al celui mai mare divizor comun (CMMDC). El este denumit după matematicianul grec Euclid, care l-a inventat. Un avantaj important al algoritmului lui Euclid este că el poate găsi CMMDC eficient fără să trebuiască să calculeze factorii primi ai numerelor.
Euclid a observat că CMMDC al două numere a și b rămîne același dacă se scade numărul mai mic din cel mai mare (demonstrați!). Presupunînd că a este numărul mai mare, scăzînd în mod repetat pe b din a, în a va rămîne restul împărțirii lui a la b. Rezultă că CMMDC(a, b) este totuna cu CMMDC(b, a % b). Algoritmul care rezultă este următorul: luăm restul împărțirii lui a la b, apoi restul împărțirii lui b la rest, și așa mai departe, pînă ce obținem un rest zero. CMMDC este numărul rămas, cel diferit de zero.
Exemplu Să calculăm CMMDC(252, 105). Calculăm 252 % 105 = 42. De aceea va trebui să calculăm CMMDC(105, 42). În continuare calculăm 105 % 42 = 21. Deci, vom calcula CMMDC(42, 21). Calculăm 42 % 21 = 0. Deoarece restul este zero CMMDC va fi ultimul număr nenul, adica 21.
Algoritmul ce foloseste structura while do
| Pseudocod | C | C++ |
|---|---|---|
citeste a,b; while( b <> 0 ) r ← a mod b; a ← b; b ← r; scrie a |
#include<stdio.h>
int main(){
int a,b,r;
scanf("%d%d",&a,&b);
while( b > 0){
r = a % b;
a = b;
b = r;
}
printf("%d", a);
return 0;
} |
#include <iostream>
using namespace std;
int main(){
int a,b,r;
cin>> a >> b;
while( b > 0 ){
r = a % b;
a = b;
b = r;
}
cout << a;
return 0;
} |
Algoritmul ce foloseste structura do while
| Pseudocod | C | C++ |
|---|---|---|
citeste a,b; do r ← a mod b; a ← b; b ← r; while( r <> 0 ) scrie a |
#include<stdio.h>
int main(){
int a,b,r;
scanf("%d%d",&a,&b);
do{
r = a % b;
a = b;
b = r;
}while( r != 0)
printf("%d", a);
return 0;
} |
#include <iostream>
using namespace std;
int main(){
int a,b,r;
cin>> a >> b;
do{
r = a % b;
a = b;
b = r;
}while( r != 0 )
cout << a;
return 0;
} |
CMMMC
#include <stdio.h>
int main(){
long long a, b, r, ca, cb;
scanf( "%lld", &a );
scanf( "%lld", &b );
ca = a;
cb = b;
while(b != 0){
r = a % b;
a = b;
b = r;
}
printf("%lld", ca * cb / a );
return 0;
}Aplicatie: Doi prieteni, un iepure și o broscuță joacă un joc: pornesc de la o linie de start și încep să sară. Broasca sare n centimetri, iar iepurele m centimetri. Cine este mai în spate vine la rînd să sară. Jocul se termină atunci cînd iepurele și broasca sînt iarăși la egalitate. Cîți centimetri au parcurs cei doi prieteni?
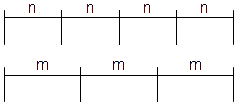
Răspuns: după cum se vede și din figură, broscuța și iepurele vor sări o lungime egală cu CMMMC(m, n). Precum știm
CMMMC(m, n) = m ∙ n / CMMDC(m, n)
.
Tema 12
Descompunerea in factori primi:
Cmmdc / Cmmmc: