Clasa a V-a lecția 6 S6
Lectie
Structura repetitiva while do
Structura repetitivă de tip WHILE-DO (cîtă timp - execută) reprezinta structura de control cu ajutorul careia executam un set de instructiuni, de mai multe ori, in functie de o conditie. Conditia se testeaza imediat la intrarea in structura repetitiva, de aceea, “while-do” se numeste structura repetitiva conditionata anterior.
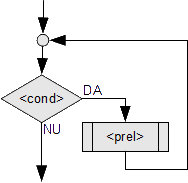
Pseudocod
Cat_timp(cond)executa Prel
C/C++
while(cond){
Prel;
}
Mecanism:
- Pas1. Se testeaza conditia. Daca conditia este adevarata atunci trecem la pasul 2. Daca conditia este falsa se trece la pasul 3
- Pasul 2: Se executa pachetul de instructiuni “Prel” si se revine la pasul 1.
- Pasul 3. Stop
Aplicatii cu while do
Afisare cifre in ordine inversa
Se citește n. Să se afișeze cifrele lui n în ordine inversă.
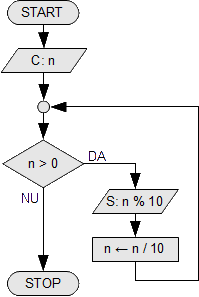
Acest algoritm de PARCURGERE a cifrelor unui numar, se va aplica problemelor care prelucreaza intr-un fel sau altul cifrele numarului respectiv. Pentru a putea parcurge cifrele unui numar, accesam mai intai cifra care se poate extrage cel mai usor din numar, si anume ultima cifra (stim ca ultima cifra a oricarui numar este restul impartirii numarului respectiv la 10). Dupa ce am extras aceasta cifra si am afisat-o , eliminam aceasta cifra din numar, astfel incat, penultima cifra a numarul va deveni ultima cifra, si deci o vom putea extrage usor si pe aceasta, la pasul urmator.
Pseudocod
intreg n Citeste n Cat_timp(n>0)executa scrie n mod 10 n = n div 10
C:
#include<stdio.h>
int main(){
int n;
printf( "Dati un numar: " );
scanf( "%d", &n );
printf( "Cifrele in ordine inversa: " );
while(n > 0){
printf( "%d", n % 10 );
n = n / 10;
}
return 0;
}C++:
#include <iostream>
using namespace std;
int main(){
int n;
cout << "Dati un numar:";
cin >> n;
cout << "Cifrele in ordine inversa:";
while( n > 0 ){
cout << n % 10;
n = n / 10;
}
return 0;
}Suma cifrelor unui numar
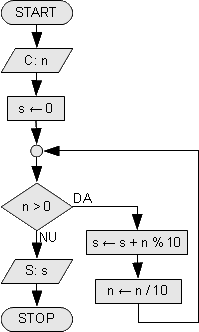
Acest algoritm, se bazeaza pe algoritmul de parcurgere a cifrelor unui numar, descris anterior. Vom avea nevoie in plus, de o variabila ACUMULATOR (o vom denumi s, de la suma), variabila in care vom aduna pe rand valorile cifrelor accesate. Pe masura ce accesam o cifra a unui numar, adunam valoarea cifrei la valoarea anterioara a acumulatorului, care valoare, este initial 0. Daca am fi dorit sa calculam produsul cifrelor unui numar, cat ar fi trebuit sa fie initial variabila acumulator?
Pseudocod
intreg n, s citeste n s = 0 cat_timp( n > 0 )executa s <- s + n mod 10 n <- n / 10 scrie s
C
include<stdio.h>
int main(){
int n,s;
scanf("%d",&n);
s=0;
while(n>0){
s= s + n % 10;
n=n/10;
}
printf("%d",s);
return 0;
}Cate cifre are un numar
Acest algoritm, se bazeaza pe algoritmul de parcurgere a cifrelor unui numar, descris anterior. Vom avea nevoie in plus, de o variabila CONTOR , cu ajutorul caruia vom numara cifrele pe masura ce le vom parcurge. Vom parcurge cifrele numarului incepand cu ultima cifra , si pentru fiecare cifra accesata, vom mari valoarea contorului cu 1.
Pseudocod
contor = 0
cat_timp( n > 0 )executa
contor <- contor + 1
n = n / 10
scrie contor
C
cnt=0;
while(n>0){
cnt++; //cnt=cnt+1; cnt+=1
n=n/10;
}
printf("%d",contor);Cate cifre sunt egale cu o cifra k
Acest algoritm, se bazeaza pe algoritmul de parcurgere a cifrelor unui numar, descris anterior. De asemenea, vom avea nevoie sa numaram cifrele care indeplinesc conditia data, folosind o variabila contor. In plus, vom avea nevoie sa testam daca o anumita cifra indeplineste conditia ceruta, si numai daca conditia este adevarata sa marim valoarea contorului.
Pseudocod
contor=0;
cat_timp(n>0)executa
daca( n mod 10 == k)
contor <- contor+1
n = n / 10
scrie contor
C
contor=0;
while(n>0){
if( n % 10 == k)
contor++;
n=n/10;
}
printf(“%d”,contor);Sunt toate cifrele lui n pare?
Acest algoritm, se bazeaza pe algoritmul de parcurgere a cifrelor unui numar, descris anterior. Vom avea nevoie in plus, de o variabila STEAG (SEMN) , cu ajutorul caruia vom identifica daca numarul are o cifra care nu respecta conditia data. Vom parcurge toate cifrele numarului si de fiecare data cand vom gasi o cifra care nu respecta conditia( nu este para) vom seta valoarea steguletului pe 0 (codificare a raspunsului NU, nu este ok numarul). Initial valoarea steguletului va fi setata pe 1 (codificare a raspunsului DA; presupunem ca numarul are numai cifre pare, adica este ok) Variabila cu rol de steag este gasit.
Pseudocod
gasit=1;
cat_timp(n>0)executa
daca( n mod 2 == 1)
gasit=1
n<-n div 10;
daca (gasit==0)
scrie “nu sunt toate pare”
altfel
scrie “sunt toate pare”
C
gasit = 1;
while( n > 0 ){
if( n % 2 == 1 )
gasit = 0;
n=n/10;
}
if( gasit == 0 )
printf(“nu sunt toate pare”);
else
printf(“sunt toate pare”);Varianta condensata:
while( n > 0 && n % 2 == 0 ){
n=n/10;
}
if( n > 0 )
printf("nu sunt toate pare");
else
printf("sunt toate pare");Inversul unui numar

#include <stdio.h>
int main() {
int n, r;
scanf( "%d", &n );
r = 0;
while ( n > 0 ) {
r = r * 10 + n % 10;
n = n / 10;
}
printf( "%d\n", r );
return 0;
}Palindrom
Definiție: un număr palindrom (sau simetric) este un număr care este identic cu răsturnatul lui. Cu alte cuvinte el arată la fel dacă îi scriem cifrele de la stînga la dreapta sau de la dreapta la stînga. Exemple de numere palindrom sînt 1221, 5229225, 27272, 44, 1. Problemă: să se determine dacă un număr n este palindrom. Rezolvare: vom calcula răsturnatul lui n în variabila r. Dacă cele două numere sînt egale înseamnă ca numărul este palindrom. Trebuie să acordăm atenție faptului că n va fi distrus în timpul calculului, drept pentru care îi vom face o copie în nc.
#include <stdio.h>
int main() {
int n, nc, r;
scanf( "%d", &n );
nc = n;
r = 0;
while ( n > 0 ) {
r = r * 10 + n % 10;
n = n / 10;
}
if ( nc == r )
printf( "%d este palindrom\n", nc );
else
printf( "%d nu este palindrom\n", nc );
return 0;
}TEMA6
- (usoara) Sa se calculeze 2 la puterea n.
- (medie) Se citeste un numar n, de maxim 9 cifre dintr-un fisier "date.in". Afisati numarul care contine, in aceeasi ordine doar cifrele pare ale lui n, intr-un fisier "date.out". Ex: n= 12345, Se va afisa 24;
- (usoara) Se citeste un numar n. Afisati numarul rezultat prin eliminarea primei cifre a lui n.
- (medie) Se citeste un numar n. Afisati cifra de control a numarul n. Cifra de control se obtine prin adunarea repetata a cifrelor numarului pana cand se obtine o singura cifra.
Ex: n=193, s=1+9+3=13, s=1+3=4
- (dificila) Se citeste un numar n. Sa se afiseze cel mai apropiat fata de n numar palindrom.
Ex1: 122 , afisam 121; nr 122 e cuprins intre 121 si 131, iar 121 este mai apropiat fata de 122 Ex2: 452 , afisam 454; nr 452 este cuprins intre 444 si 454.
Optional
Util
- Citire/ scriere in C/c++ Citire/Scriere
- Instalare codeblocks Code::Blocks.