Clasa a V-a lecția 8 - 23 oct 2012

From Algopedia
Jump to navigationJump to search

Introducere

  • Nu mai folosiți elemente pe care nu le-ați învățat: vă bănuiesc că vă face altcineva tema!
  • Din structura repetitivă de tip WHILE-DO se iese prin josul rombului, nu prin lateral!

Tema - verificare

  • Felicitări pentru instalarea CodeBlocks! Cei ce nu ați reușit v-am dat instrucțiuni. Dacă nu reușiți în continuare veniți cu laptopul data viitoare.
  • Nu am reluat tema la tablă deoarece era simplă. Scopul exercițiilor a fost să vă obișnuiască cu CodeBlocks.

Lecție

Limbajul C

  • Instrucțiunea if. Operatorii de comparație ==, !=, <, <=, >, >=. Exercițiu:
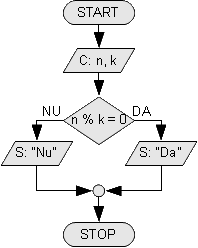
    • Să se spună dacă n divizibil cu k
Schemă logică
 
#include <stdio.h>

int main() {
  int n, k;

  scanf( "%d%d", &n, &k );
  if ( n % k == 0 )
    printf( "Da" );
  else
    printf( "Nu" );
  return 0;
}
  • Instrucțiunea compusă, acolade. Exercițiu:
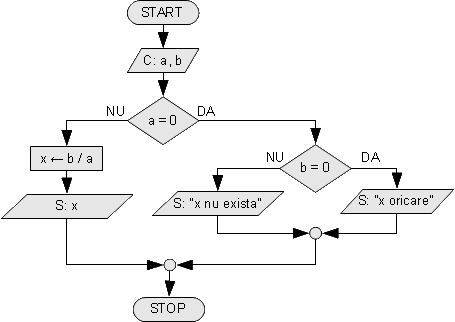
    • Ecuația de gradul 1
Schemă logică
 
#include <stdio.h>

int main() {
  int a, b, x;

  scanf( "%d%d", &a, &b );
  if ( a == 0 )
    if ( b == 0 )
      printf( "x oricare\n" );
    else
      printf( "x nu exista\n" );
  else {
    x = b / a;
    printf( "x este %d\n", x );
  }
  return 0;
}
  • Exerciții cu if-uri unul într-altul (numite și if-uri imbricate):
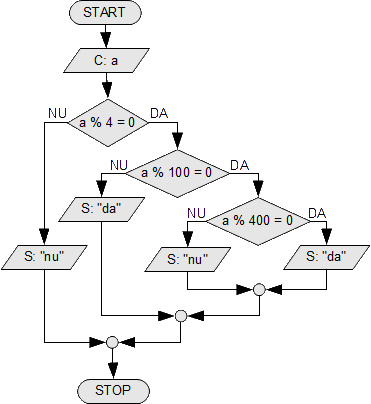
    • Să se spună dacă un an este bisect
Schemă logică
 
#include <stdio.h>

int main() {
  int a;

  scanf( "%d", &a );
  if ( a % 4 == 0 )
    if ( a % 100 == 0 )
      if ( a % 400 == 0 )
        printf( "da\n" );
      else
        printf( "nu\n" );
    else
      printf( "da\n" );
  else
    printf( "nu\n" );
  return 0;
}
  • Instrucțiunea while. Exerciții:
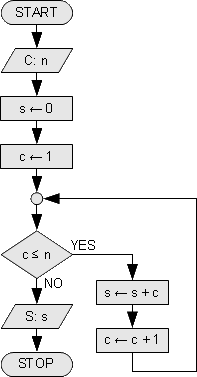
    • Suma numerelor de la 1 la n fără Gauss
Schemă logică
 
#include <stdio.h>

int main() {
  int n, s, c;

  scanf( "%d", &n );
  s = 0;
  c = 1;
  while ( c <= n ) {
    s = s + c;
    c = c + 1;
  }
  printf( "Suma este %d\n", s );
  return 0;
}
    • Să se afișeze suma cifrelor lui n
Schemă logică
 
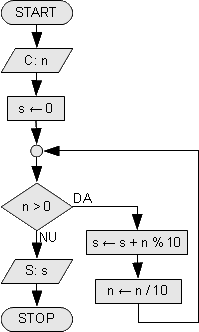 #include <stdio.h>

 int main() {
   int n, s, c;

   scanf( "%d", &n );
   s = 0;
   while ( n > 0 ) {
     s = s + n % 10;
     n = n / 10;
   }
   printf( "Suma este %d\n", s );
   return 0;
 }
    • Să se afișeze inversul lui n
Schemă logică
 
 #include <stdio.h>

 int main() {
   int n, r;

   scanf( "%d", &n );
   s = 0;
   while ( n > 0 ) {
     r = r * 10 + n % 10;
     n = n / 10;
   }
   printf( "Rasturnatul lui n este %d\n", r );
   return 0;
 }

Tema

  • Să se rezolve următoarele probleme (schemă logică + program C în CodeBlocks):
    • Calculați x11 cu număr minim de înmulțiri: Care este numărul minim?
    • Se citește un număr n. Să se spună cîte cifre pare are el. Exemple: dacă n=3528 el are 2 cifre pare (2 și 8), dacă n=49285640 el are 6 cifre pare (4, 2, 8, 6, 4, 0).
    • Se citește un număr n. Să se afișeze cel mai mare divizor propriu al lui n (strict mai mic decît n). Exemplu: dacă n=24 cel mai mare divizor propriu este 12. Dacă n=125 cel mai mare divizor propriu este 25. Dacă n = 175 cel mai mare divizor propriu este 35.
  • Problemă de logică: filozoful Immanuel Kant a ajuns acasă unde a constatat că ceasul de perete a stat deoarece a uitat să-l întoarcă. El a plecat către prietenul lui bun. Acolo a stat o vreme la discuții filozofice, apoi s-a întors înapoi acasă unde a potrivit ceasul la ora exactă! Cum a procedat Kant? Se știe că:
    • Prietenul lui Kant are un ceas care merge bine
    • Pe vremea lui Kant nu existau ceasuri de mînă sau alte dispozitive mobile cu ceas
    • Kant merge cu viteză constantă, de ani de zile aceeași.

Rezolvări aici [1]

Retrieved from "https://www.algopedia.ro/wiki/index.php?title=Clasa_a_V-a_lecția_8_-_23_oct_2012&oldid=7339"