Clasa a V-a lecția 9 - 5 oct 2017

Comentarii la rezolvările la teme

Atenţie: în legătură cu programele C pe care le aveţi la temă: trebuie să le introduceţi în Code::Blocks şi să le testaţi că funcţionează corect. Scopul acestor teme este ca voi să vă familiarizaţi cu programarea. Nu puteţi face aceasta doar scriind programe pe hîrtie! Constat că unii dintre voi încă nu au scris nici un program la calculator. Cei care nu intraţi rapid în ritm, nu începeţi să programaţi la calculator, să vă verificaţi şi corectaţi programele, veţi rămîne în urmă.

Repet: rezolvarea unei probleme la temă constă în scrierea unei scheme logice, abia apoi transcrierea ei în program C, introducerea acestui program în Code::Blocks, verificarea corectitudinii prin execuţia pe cîteva teste şi corectarea greşelilor. Aceasta înseamnă că va trebui să vă gîndiţi voi la teste, pentru verificare.

Tema - rezolvări

Rezolvări aici [1]

Lecție

<html5media height="720" width="1280">https://www.algopedia.ro/video/2017-2018/2017-10-05-lectie-info-09-720p.mp4</html5media>

Am făcut schema logică și programul C pentru următoarele exerciții:

Exercițiul 1 - palindrom

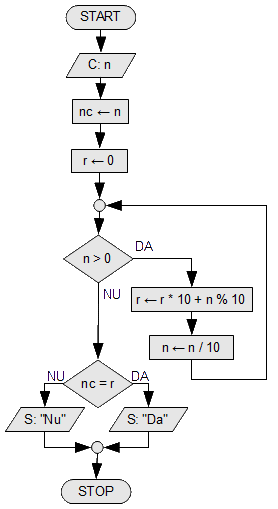
Se citește un număr n. Să se spună dacă n este palindrom. Un număr este palindrom dacă prima lui cifră este egală cu ultima, a doua cu penultima și așa mai departe. Exemple de palindroame: 15351, 7337 sau 12233221.

Pentru a rezolva exerciţiul am observat următoarea proprietate: inversul unui număr palindrom este egal cu numărul original. Schema logică calculează inversul numărului n în variabila r şi apoi compară r cu originalul. Deoarece variabila n este modificată pe parcursul caculului, vom memora o copie a ei in variabila nc.

Palindrom

#include <stdio.h> int main() { int n, nc, r; scanf( "%d", &n ); nc = n; r = 0; while ( n > 0 ) { r = r * 10 + n % 10; n = n / 10; } if ( nc == r ) printf( "%d este palindrom\n", nc ); else printf( "%d nu este palindrom\n", nc ); return 0; }

Exerciţiul 2 - divizorii unui număr

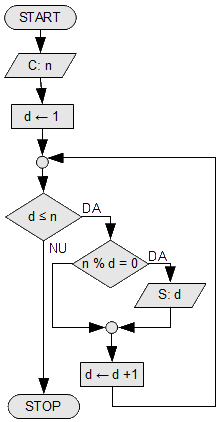
Se citește un număr n, să se afișeze toți divizorii lui n. Spunem că d este divizor al lui n dacă n se împarte la d.

Pentru a rezolva exerciţiul vom varia un contor d de la 1 la n. El reprezintă potenţialii divizori ai lui n. Pentru fiecare valoare a lui d vom testa dacă n se împarte la d. Dacă da, vom afişa acel divizor.

Divizorii lui n

#include <stdio.h> int main() { int n, d; scanf( "%d", &n ); printf( "Divizorii lui %d sint:", n ); d = 1; while ( d <= n ) { if ( n % d == 0 ) printf( " %d", d ); d = d + 1; } printf( "\n" ); return 0; }

Observație: între n/2 și n nu mai avem nici un divizor, deci am putea optimiza algoritmul punînd condiția while ( d <= n / 2 ) și afișînd n, ultimul divizor, separat, în afara buclei while

Modificare

O modificare ușoară a exerciţiului este: se citește un număr n. Să se afișeze toți divizorii impari ai lui n. Singura diferență este că vom adăuga 2 la d în loc de 1:

d ← d + 2

Operatori logici

Condițiile care apar în blocurile de decizie (romburi) și în instrucțiunile if și while din C pot fi compuse folosind următorii operatori logici: și, sau și not (în scheme logice), sau &&, || și ! În limbajul C. Iată exemple de folosire în următoarele exerciții:

Exerciţiul 3 - număr prim

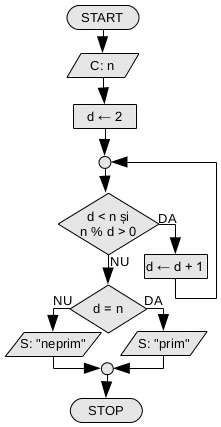
Se citește un număr n. Să se spună dacă n este prim. Un număr este prim dacă nu se împarte decît la 1 și la el însuși.

Vom proceda similar cu afişarea divizorilor: vom căuta primul divizor al lui n, începînd cu 2. Dacă găsim un divizor numărul nu este prim. Dacă, în schimb, primul divizor găsit este chiar n, numărul este prim.

Număr prim

#include <stdio.h> int main() { int n, d; scanf( "%d", &n ); d = 2; while ( d < n && n % d > 0 ) d = d + 1; if ( d == n ) printf( "%d este prim\n", n ); else printf( "%d nu este prim\n", n ); return 0; }

Observații:

1. Avem cu adevărat nevoie de condiția d < n? Justificați răspunsul.
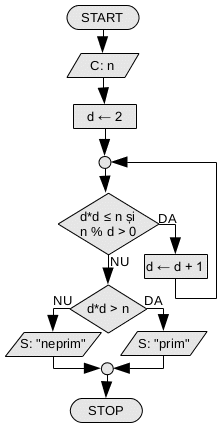
2. Putem face mai puține iterații dacă observăm că dacă un număr nu are nici un divizor strict mai mare ca 1 dar mai mic sau egal cu radical din n atunci el nu va avea nici alți divizori mai mari decît radical din n dar mai mici decît n. Cum justificăm acest lucru? Putem, deci, înlocui condiția d < n cu d * d <= n. În acest caz va trebui să modificăm condiția finală de test de primalitate din d == n în d * d > n.

Iată algoritmul modificat:

Număr prim

#include <stdio.h> int main() { int n, d; scanf( "%d", &n ); d = 2; while ( d * d <= n && n % d > 0 ) d = d + 1; if ( d * d > n ) printf( "%d este prim\n", n ); else printf( "%d nu este prim\n", n ); return 0; }

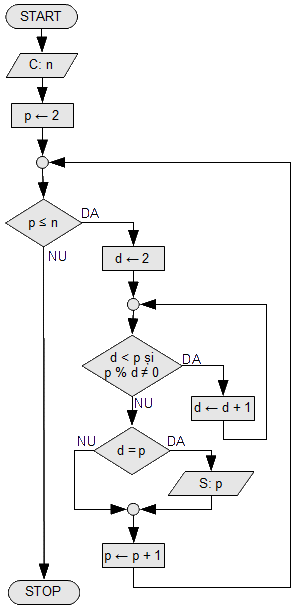
Exerciţiul 4 - numere prime pînă la n

Se citește un număr n. Să se afișeze toate numerele prime mai mici sau egale cu n.

Vom folosi exerciţiul anterior. Vom varia un contor p de la 2 pînă la n. Aceste numere pot sau nu să fie numere prime, drept pentru care vom testa fiecare din ele dacă este prim.

Numere prime pînă la n

#include <stdio.h> int main() { int n, p, d; scanf( "%d", &n ); printf( "Nr. prime pina la %d:", n ); p = 2; while ( p <= n ) { d = 2; while ( d < p && p % d > 0 ) d = d + 1; if ( d == p ) printf( " %d", p ); p = p + 1; } printf( "\n" ); return 0; }

Observație: acesta este primul nostru algoritm în care am folosit două bucle while imbricate (una într-alta). Interesant, nu?

Tema

• Să se rezolve următoarele probleme (schemă logică + program C executat în CodeBlocks):
  • Se citesc două numere, n și k. Să se afișeze toate numerele mai mici sau egale cu n care se divid cu k. Exemple: pentru n = 7 k = 2 se va afișa 2 4 6; pentru n = 25 k = 5 se va afișa 5 10 15 20 25.
  • Se citește un număr n. Să se afișeze toate numerele perfecte mai mici sau egale cu n. Un număr este perfect dacă este egal cu suma divizorilor lui strict mai mici ca el. Primul număr perfect este 6, deoarece 6 = 1 + 2 + 3. Următorul număr este 28 deoarece 28 = 1 + 2 + 4 + 7 + 14. Exemple: dacă n = 8 se va afișa 6. Dacă n = 30 se va afișa 6 28. Dacă n = 500 se va afișa 6 28 496.
• Problemă de logică: ce linie urmează în secvență:

       1
      1 1
      2 1
    1 2 1 1
  1 1 1 2 2 1
  3 1 2 2 1 1
1 3 1 1 2 2 2 1

Rezolvări aici [2]