Clasa a VI-a lecția 26 - 12 apr 2016
Tema - rezolvări
Lectie
Programare dinamică
Introducere
Wikipedia definește programarea dinamică drept "... o metodă pentru rezolvarea unor probleme complexe prin descompunerea lor în subprobleme mai simple. Se poate aplica problemelor care prezintă proprietățile de suprapunere a subproblemelor și de substructură optimală. Atunci cînd se poate aplica, metoda ia mult mai puțin timp decît alte soluții naive.
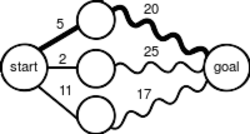
Substructura optimală înseamnă că soluția unei problemei de optimizare date poate fi obținută prin combinarea unor soluții optimale ale subproblemelor. Ca atare, primul pas către găsirea unei rezolvări prin această metodă este verificarea dacă problema are proprietatea substructurii optimale. Astfel de substructuri optimale sînt în mod uzual descrise prin recurență. De exemplu, date niște orașe și distanțele între ele, drumul cel mai scurt de la orașul u la orașul v are proprietatea de substructură optimală: să luăm orice oraș intermediar w pe drumul cel mai scurt, d. Dacă d este cu adevărat drumul cel mai scurt, atunci drumul d1 de la u la w și d2 de la w la v sînt cu adevărat cele mai scurte drumuri între orașele corespunzătoare. Dacă drumul de la u la w nu ar fi cel mai scurt posibil ar însemna că am avea un alt drum mai scurt, ceea ce ar duce la un drum total d, de la u la v, mai scurt decît cel original. Așadar, putem formula soluția problemei găsirii celui mai scurt drum într-o manieră recursivă, ceea ce fac algoritmii Bellman-Ford și Floyd-Warshall.
Suprapunerea subproblemelor înseamnă că ele nu sînt independente, adică subproblemele au în comun alte subprobleme. Nu vom insista pe această proprietate decît atît cît să menționăm că dacă subproblemele nu se suprapun dar prezintă substructură optimală atunci putem aplica tehnica de programare divide et impera (divide and conquer). De aceea quicksort și mergesort nu sînt clasificate ca probleme de programare dinamică.
Metodă
Cînd încercăm să rezolvăm o problemă de programare dinamică întrebarea crucială la care trebuie să răspundem este putem calcula soluția finală pe baza unor subprobleme care sînt la rîndul lor optimale? Pentru a răspunde la întrebare trebuie mai întîi să formulăm subproblemele. Dar pentru a formula subproblemele trebuie să avem în minte principiul substructurii optimale. Altfel s-ar putea să împărțim problema în subprobleme care nu au substructură optimală.
Să recapitulăm: pentru a putea răspunde la întrebarea dacă o problemă admite o soluție prin programare dinamică trebuie să aflăm dacă are substructură optimală. Dar pentru a afla dacă are substructură optimală trebuie să găsim subproblemele. Pe care încercăm să le găsim folosind programarea dinamică.
Nu cumva ne învîrtim în cerc? Așa pare și așa și este, într-o oarecare măsură. Experiența este cea care ne învață cum să căutăm împarțirea în subprobleme astfel încît să obținem proprietatea de optimalitate. Tot experiența este cea care ne ajută să ne dăm seama rapid dacă împărțirea găsită are această proprietate sau nu.
Odată ce demonstrăm că o împărțire în subprobleme se bazează doar pe subprobleme optimale, restul decurge, de obicei, destul de simplu: găsim o formulă de recurență, apoi o implementăm de jos în sus (sau bottom-up), pornind de la cele mai mici probleme, către cele mai mari, pînă la soluția cerută.
Să luăm cîteva exemple.
Subsecvența crescătoare de lungime maximă
Această problemă cere să găsim o subsecvență a unei secvențe de numere în care elementele sînt în ordine crescătoare, iar subsecvența este de lungime maximă. Subsecvența nu este neapărat contiguă, nici unică.
Exemplu
În secvența
- 0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15, …
o secvență crescătoare de lungime maximă este
- 0, 2, 6, 9, 13, 15.
Această secvență are lungime șase. Nu există nici o secvență crescătoare de lungime șapte. Cea mai lungă subsecvență crescătoare nu este unică. De exemplu
- 0, 4, 6, 9, 11, 15
este o altă subsecvență crescătoare de aceeași lungime, în secvența de intrare.
Soluție
Cum împărțim problema în subprobleme? Să încercăm astfel:
- L[i] = lungimea celei mai lungi subsecvențe care începe la poziția i
Are această împărțire proprietatea de optimalitate? Să presupunem că avem o subsecvență optimală crescătoare care trece prin indicii
- i1, i2, …, ik, …, im
Este secvența i1, i2, …, ik optimală? Dar secvența ik, …, im? Amîndouă sînt optimale deoarece altfel le-am putea înlocui cu secvențe mai lungi, ceea ce ar duce la o subsecvență mai lungă decît cea inițială, care era optimală.
Următorul pas este să găsim relația de recurență:
- L[i] = max(L[j]+1), j > i și V[j] ≥ V[i]
Următorul pas este să construim subproblemele bottom-up, de la problemele mai mici la cele mai mari. Pentru aceasta vom calcula vectorul L de la coadă la cap, căutînd pentru fiecare element L[i] cel mai mare element L[j] de după el (j > i) astfel încît V[j] ≥ V[i].
Soluția problemei este maximul din vectorul L. Acest algoritm are complexitate O(n2), unde n este lungimea secvenței. Memoria folosită este O(n). Putem reconstrui o subsecvență maximală folosind încă un vector de indice următor în secvență. Există și un algoritm mai rapid, de complexitate O(n log n).
Tema
Optional (problema grea)