Clasa a VII-a lecția 10 - 14 nov 2019

Anunțuri

• Vă rog denumiți variabilele și funcțiile cu grijă. Îmi este greu să citesc programe în care funcțiile sînt denumite fără nici o noimă, gen sir1(), sir2() și 'sir3(), sau recusiv1() și recusiv2().
• Am suspiciuni că unii din voi sînt "ajutați" la teme. Prin "ajutați" a se înțelege li se face tema. Nu uitați că influențele externe sînt extrem de vizibile, după doi ani la IQ Academy. Nu vreau să fac pe polițistul. Încetați sau ne supărăm.

Tema - rezolvări

Sumprim

Problema sumprim este o problemă simplă de introducere în recursivitate. Ea cere, în principal, să se calculeze ciurul lui Eratostene recursiv, fără a folosi bucle.

Comentarii generale

• Mulți ați dat soluții bune, bravo!
• Unii ați scris ciurul neoptim, O(n log n). De aceea ați depășit timpul la teste mari.

Fibrec

Problema fibrec este o problemă tipică de recursivitate. Ea cere să se calculeze al n^lea termen din șirul lui Fibonacci folosind numere mari și fără a folosi bucle, doar apeluri recursive.

Comentarii generale

• Felicitări celor ce au reușit o soluție foarte bună și ordonată: Nicola, Voicu T, Asgari, Cadîr, Ilie, Rebengiuc, Tatomir
• Pare că vă descurcați bine cu programe recursive, bravo!
• Unii din voi ați folosit transmiterea vectorilor ca parametru pentru a interschimba vectorii fără a-i copia. Foarte drăguț!
• Mulți dintre voi au interchimbat vectorii după fiecare adunare, prin copiere. Ineficient. Ba chiar unii au folosit și un vector suplimentar! Bănuiesc că motivul este că anul trecut am prezentat o astfel de soluție. Dar atunci nu știam încă matrice! Între timp am învățat o tehnică standard în astfel de situații: folosim o matrice de două linii și o variabilă ce ia valori în {0, 1}, să-i spunem p. Vom aduna linia 1-p la p și apoi vom modifica p la 1-p. Hai să folosim ceea ce am învățat pînă acum.
• Mulți dintre voi ați afișat cifre cu fprintf. Este foarte ineficient, folosiți fputc.
• Unii din voi au stocat cifrele numerelor mari începînd de la coada vectorilor. Este incorect, revedeți vă rog lecția de numere mari de anul trecut.
• Unii din voi au stocat numărul de cifre al numerelor mari în elementul zero al vectorului de cifre. Aceasta este nu numai greșit din principiu, căci amestecăm mere cu pere, dar, în acest caz, dăunător, deoarece va trebui să declarăm vectori cu elemente short sau int. Vă rog nu procedați așa. Revedeți lecția de anul trecut de numere mari.
• Avertismente: Chivu (nici o sursă).

Comentarii individuale

Prima grupă

Din păcate nu am avut timp să scriu comentariile individuale.

A doua grupă

• Asgari: Program foarte bun, bravo! Cam multe variabile globale, dar altfel un program foarte solid!
• Cadîr: Program foarte bun, bravo! Oare prea bun? Mi-a plăcut ideea de a interschimba numerele mari la momentul calculului. Mă face să mă întreb. Nu-mi place să mă întreb, sper că nu te ajută nimeni.
• Dimulescu: Program foarte solid, bravo! Și bine indentat ;-) Observații:
  • Nu era nevoie să interschimbi vectori. Vezi mai jos cum folosim o matrice de două linii - soluție standard.
  • Nu era nevoie ca fișierele să fie variabile globale.
  • Ai un if degeaba:

  if( n > 2 )
    fibonacci( f1, f2, n1, n2, n, 3 );
  if( n <= 2 )
    fprintf( fout, "%d", 1 );

Corect era să folosești else:

  if( n > 2 )
    fibonacci( f1, f2, n1, n2, n, 3 );
  else
    fprintf( fout, "%d", 1 );

• Fares: Partea bună: funcționează. Partea rea: destul de greu de citit/corectat. Ar fi fost bune fie niște comentarii, fie niște nume de funcții mai clare, nu f() sau fun1(). Pare însă că faci un interschimb al vectorilor folosind un vector auxiliar - destul de risipitor și ia și timp. Vezi mai jos o soluție standard în care folosim o matrice de două linii. Ce este cu variabila ok? Stegulețele aiurea ne urmăresc pînă în clasa a șaptea, nu? :-)
• Ghica: Un program rezonabil. Cu următoarele observații:
  • Adunarea numerelor mari e un pic încîlcită. E mai clar și mai eficient să folosești o variabilă transport. Ar fi bine să te uiți pe lecția de numere mari de anul trecut.
  • Folosești vectori de la 1, în loc de 0 fără motiv. Strict interzis. Te rog să renunți la acest nărav.
  • Folosești un al treilea vector și copieri. Vezi te rog mai jos cum putem folosi o tehnică standard, mai eficientă, folosind doi vectori și fără copieri.
• Grecu: Program bun, bravo. Cu observațiile, unele grave:
  • Avertisment serios: funcție care ajunge la final fără să returneze ceva. Ai compilat cu -O2 și -Wall?
  • Ai return în mai multe locuri în funcție, fără a fi cazuri de terminare recursivitate. Nu e OK.
  • Ideea de a folosi variabila turn este bună. Dar nu ai parametrizat. De aceea ai multe teste repetitive.
  • Cel mai grav pentru punctaj: folosești fprintf pentru a tipări caractere. Extrem de lent. Bănuiesc că de aceea depășești timpul.
• Ilie: Program foarte bun, bravo! În loc de huge() i-aș fi spus add().
• Ipate: Program foarte bun, bravo! E surprinzător că te încadrezi în timp cînd folosești fprintf() pentru a tipări cifre. Atenție mare! În loc de bucla() i-aș fi spus aduna(), pentru claritate. Mi-a plăcut ideea de a interschimba numerele mari la momentul calculului. Vezi mai jos cum poți face standard, fără interschimbare.
• Marcu: Program foarte bun, bravo! Ai multe avertismente, atenție la ele! Ai interschimbat numerele mari. Anul trecut am discutat o tehnică pentru a nu face asta. Vezi te rog mai jos. Ai efectuatu partea finală din adunarea numerelor (verificarea că ai o cifră în plus) în altă funcție. Foarte neelegant. Funcțiile trebuie să facă ceea ce promit să facă. Dacă fac adunare, ar fi bine să o facă pînă la capăt, nu? :-)
• Moroșan: Un program rezonabil, bravo! Faci mereu adunarea pe 6000 de cifre. La început numerele sînt mult mai mici. Cred că acesta este și motivul pentru care depășești timpul. Ar fi bine să te uiti pe lecția de numere mari de anul trecut. Singura obiecție majoră este funcția de afișare, scrisă încîlcit și cu stegulețe.
• Nicu: Un program bun, bravo! Observații, unele grave:
  • Folosești fprintf() pentru a scrie cifre. De mirare că te încadrezi în timp.
  • Folosești copieri și vectori suplimentari. Am discutat despre soluții mai eficiente anul trecut. Vezi te rog soluția de mai jos.
  • Ai declarat vectorii cu unu în plus. De ce? Ne supărăm.
• Petrescu: Un program solid, se vede că ai înțeles recursivitatea, bravo! Observații:
  • Ai multe, multe avertismente de compilare, unele grave. Returnezi vectori, dar funcția e declarată ca returnînd întregi.
  • Ai return în multe locuri în funcții. Nu este OK, am discutat asta!
  • Memorezi numerele mari în ordine inversă. Vezi te rog lecția de numere mari de anul trecut.
  • Ai grijă în ce ordine scrii funcțiile. O funcție nu poate chema o altă funcție scrisă mai jos în program. Schimbă-le ordinea.
  • Afișezi cifre cu fprintf(), foarte ineficient! Folosește fputc().
• Popescu: Program foarte bun, bravo! Ai calculat numărul maxim de cifre, drăguț! Nu copiezi vectori, bravo! Ca observații:
  • Ai avertismente de compilare. Ai grijă să setezi mereu -Wall și -O2 și să te uiți la rezultatele compilării în CodeBlocks!
  • Afișezi cifre cu fprintf(), foarte ineficient! Folosește fputc().
• Rebengiuc: Program foarte bun, bravo! Un exercițiu în struct și pointeri, nu? :-) Ca observație minoră, condiția ca i să nu depășească MAX_CF este inutilă, nu-i așa? Știm că numărul nu va depăși acele cifre.
• Rughiniș: Un program foarte bun, bravo! Mi-a plăcut ideea de a interschimba numerele mari la momentul calculului.
  • În loc de operatii() i-aș fi spus adunare(), nu? E mai clar ce face funcția.
  • Afișezi cifre cu fprintf(), foarte ineficient! Folosește fputc().
• Stancu: Programul are o formă rezonabilă. Trebuia să îl depanezi.
• Tatomir: Program foarte bun, bravo! Observații:
  • Ai avertisment de compilare. main() nu returnează nici o valoare. Atenție la avertismente :-)
  • Cam multe variabile globale, care fac codul greu de urmărit, păcat.
  • Funcția bg() adună, aș fi denumit-o adun().
  • Funcția de adunare nu face doar adunare. La final schimbă poz. Nu este elegant, ea trebuia să facă doar adunare. Schimbarea lui poz ar trebui să se întîmple în rez().
• Teodorescu: Program foarte bun, bravo! Ca observații:
  • Ai avertismente de compilare, unele grave! Nu uita să setezi -Wall și -O2 și să te uiți la rezultatele compilării!
  • formare() este de fapt adunare(). Încerci să vezi dacă mă prind?
  • Funcția de adunare nu adună pînă la capăt. Ultima parte, cînd numărul crește cu o cifră, o faci în funcția apelantă. Nu este deloc elegant, o funcție trebuie să aibă un sens.
• Voicu: Program bun, bravo! Stăpînești bine recursivitatea. Observații:
• Atenție, funcția whatRemains pare inutilă. Ea nu se va reapela niciodată, deoarece transportul nu poate depăși valoarea 1, nu?
• Adunarea de numere mari este încîlcită. Vezi te rog lecția de anul trecut de numere mari.
• Ai declarat vectorii de 6001 elemente. De ce nu 6000?

Apariții 2

Problema aparitii2 este una de introducere în recursivitate. Ea cere să rezolvăm o problemă clasică, aceea de căutare a unui subșir într-un șir, folosind recursivitatea pentru a înlocui buclele.

Rezolvări aici [1]

Lecție - recursivitate, încheiere

<html5media height="720" width="1280">https://www.algopedia.ro/video/2019-2020/2019-11-14-clasa-7-lectie-info-10-720p.mp4</html5media>

Fill recursiv (flood fill)

Introducere

Algoritmul fill "umple" toate golurile accesibile de la un punct dat. Golurile pot fi elemente zero intr-o matrice, de exemplu, iar vecinii pot fi definiți ca elementele adiacente pe linie și coloană (acesta este cazul cel mai întîlnit). Alteori vecinii pot fi definiți ca avînd un punct comun cu elementul curent, ceea ce include și elementele alăturate pe diagonală. Să luăm un exemplu clasic:

Se dă o matrice a[m][n] cu elemente 0 și 1, 0 semnificînd liber și 1 semnificînd zid, precum și o poziție în matrice, (l, c). Să se spuna cîte elemente 0 sînt accesibile de la (l, c) avansînd doar pe linie sau pe coloană.

int fill( int l, int c ) {          // umple de la coloana l, c
  int suma = 1;                     // contorizam punctul curent

  a[l][c] = 1;                      // marcam pozitia ca parcursa
  if ( l > 0 && a[l-1][c] == 0 )    // ne deplasam in sus
    suma += fill( l - 1, c );
  if ( l < m-1 && a[l+1][c] == 0  ) // ne deplasam in jos
    suma += fill( l + 1, c );
  if ( c > 0 && a[l][c-1] == 0  )   // ne deplasam spre stinga
    suma += fill( l, c - 1 );
  if ( c < n-1 && a[l][c+1] == 0  ) // ne deplasam spre dreapta
    suma += fill( l, c + 1 );

  return suma;
}
...
int main() {
  int suma;
  ...
  suma = 0;
  if ( a[l][c] == 0 )
    suma = fill( l, c );
  printf( "%d", suma );
  ...
}

Observații:

• Ordinea direcțiilor nu contează. Cele patru apeluri recursive pot fi în orice ordine.
• Vecinii pot fi în număr de 4 - cei adiacenți pe linie și pe coloană, ca în exemplul de mai sus, sau pot fi în număr de 8 - și cei adiacenți pe diagonale.

Ce complexitate are acest algoritm?

Acest algoritm are complexitate O(m·n) ca timp, deoarece poate parcurge toate elementele matricei, iar prelucrarea per element este O(1). Memoria ocupată este de asemenea O(m·n) deoarece fiecare apel recursiv necesită O(1) memorie și putem avea O(m·n) apeluri recursive unul în altul.

Atenție! Acesta este principalul impediment al metodei! Ea folosește foarte multă memorie suplimentară.

Exemplificare grafică

Să vedem niște vizualizări ale algoritmului flood fill preluate de la wikipedia: algoritm flood fill:

Flood fill cu 4 direcții

Flood fill cu 8 direcții

Exemplu mare de flood fill cu 4 direcții

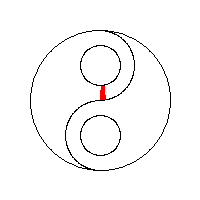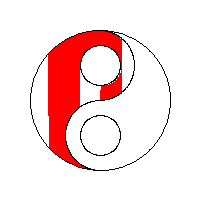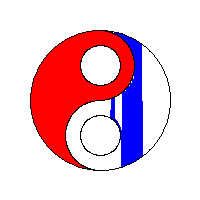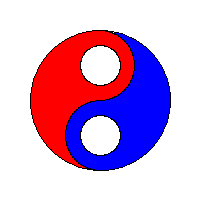
Optimizări

Bordare matrice

O primă optimizare de timp este clasică. Pentru a face programul atît mai rapid cît și mai scurt putem borda matricea de jur împrejur cu elementul zid, în cazul nostru 1. Astfel vom scuti testul de ieșire a coordonatelor din matrice. Funcția se simplifică:

int fill( int l, int c ) { // umple de la coloana l, c
  int suma = 1;               // contorizam punctul curent

  a[l][c] = 1;                // marcam pozitia ca parcursa
  if ( a[l-1][c] == 0 )       // ne deplasam in sus
    suma += fill( l - 1, c );
  if ( a[l+1][c] == 0  )      // ne deplasam in jos
    suma += fill( l + 1, c );
  if ( a[l][c-1] == 0  )      // ne deplasam spre stinga
    suma += fill( l, c - 1 );
  if ( a[l][c+1] == 0  )      // ne deplasam spre dreapta
    suma += fill( l, c + 1 );

  return suma;
}

Reducere memorie folosită

Cum calculăm memoria ocupată? Țineți minte: fiecare apel recursiv ocupă memorie echivalentul unui int. Pe un calculator de 32 de biți, cum sint cele pe care lucrăm noi (ele sînt de fapt de 64 de biți, dar programele sînt compilate în modul 32 de biți), aceasta înseamnă patru octeți. Aceasta este adresa de întoarcere din funcție. Alte elemente care ocupă memorie pe stivă sînt parametrii transmiși și variabilele declarate în funcție. În cazul nostru vom avea 16 octeți cei doi parametri, variabila declarată în funcție și adresa de întoarcere din funcție.

Dacă micșorarea memoriei folosite este esențială putem elimina 12 octeți din 16, declarînd variabilele l, c și suma globale, astfel:

int l, c, suma; // variabile globale
...
void fill() {
  suma++;
  a[l][c] = 1;
  l--;
  if ( a[l][c] == 0 ) // apelam pentru (l - 1, c)
    fill();
  l++;
  l++;
  if ( a[l][c] == 0 ) // apelam pentru (l + 1, c)
    fill();
  l--;
  c--;
  if ( a[l][c] == 0 ) // apelam pentru (l, c - 1)
    fill();
  c++;
  c++;
  if ( a[l][c] == 0 ) // apelam pentru (l, c + 1)
    fill();
  c--;                // acum (l, c) sint cele de la inceput
}

Este o modificare urîtă, care face codul nelizibil, dar uneori necesară la olimpiadă. Nu uitați că chiar și în această formă algoritmul va folosi 4 octeți pe apel recursiv imbricat pentru adresa de revenire din funcție.

Observație: variabilele l și c fiind globale ele trebuie să aibă aceeași valoare la ieșirea din funcție ca și la intrarea în funcție. De aceea ultima instrucțiune c--; este importantă!

Aplicații

Găsire ieșire din labirint

Folosind flood fill putem găsi un punct de ieșire dintr-un labirint memorat într-o matrice. Să presupunem că elementele '0' înseamnă loc gol și cele '1' înseamnă zid. Ieșirile sînt puncte '0' pe marginile matricei. Dat un punct din interiorul matricei, există un drum spre ieșire? Dacă da putem găsi atît coordonatele ieșirii cît și drumul parcurs.

Iată un exemplu de program care afișează coordonatele ieșirii:

int fill( int l, int c ) {
  int retval;

  if ( lab[l][c] == BORDER ) // am ajuns la margine?
    return l * MAXN + c;     // returnam (l, c)
    
  lab[l][c] = 1;                   // marcam punctul curent ca vizitat
  retval = 0;                      // 0 inseamna ca nu am gasit iesire
  if ( lab[l + 1][c] != 1 )        // daca nu este zid
    retval = fill(l + 1, c);       // cautam in jos
  if ( retval == 0 ) {             // daca nu am gasit iesire
    if ( lab[l - 1][c] != 1 )      // si nu este zid
      retval = fill(l - 1, c);     // cautam in sus
    if ( retval == 0 ) {           // daca nu am gasit iesire
      if ( lab[l][c + 1] != 1 )    // si nu este zid
        retval = fill(l, c + 1);   // cautam in dreapta
      if ( retval == 0 )           // daca nu am gasit iesire
        if ( lab[l][c - 1] != 1 )  // si nu este zid
          retval = fill(l, c - 1); // cautam in stinga
    }
  }

  return retval;
}

int main() {
  FILE *fin, *fout;
  int n, l, c, ls, cs, p;

  fin = fopen( "iesire.in", "r" );
  fscanf( fin, "%d%d%d ", &n, &ls, &cs );
  for ( l = 0; l < n; l++ ) {
    for ( c = 0; c < n; c++ )     // citim linia l a matricei
      lab[l][c] = fgetc( fin ) - '0';
    fgetc( fin ); // citim '\n'
  }
  fclose( fin );
  for ( c = 0; c < n; c++ ) { // bordare conditionala margini
    if ( lab[0][c] == 0 )
      lab[0][c] = BORDER; 
    if ( lab[n - 1][c] == 0 )
      lab[n - 1][c] = BORDER;
    if ( lab[c][0] == 0 )
      lab[c][0] = BORDER;
    if ( lab[c][n - 1] == 0 )
      lab[c][n - 1] = BORDER;
  }

  p = fill( ls - 1, cs - 1 );
  
  fout = fopen( "iesire.out", "w" );
  if ( p > 0 )
    fprintf( fout, "%d %d\n", 1 + p / MAXN, 1 + p % MAXN );
  else
    fprintf( fout, "-1\n" );
  fclose( fout );

  return 0;
}

Arie goluri

Calcul arie goluri: dorim să aflăm numărul de elemente zero accesibile din punctul inițial.

Iată un exemplu de program care afișează aria golului accesibil din punctul inițial:

#include <stdio.h>

#define MAXN 1000
#define BORDER 2

char lab[MAXN + 2][MAXN + 2]; // matricea labirint

// Executa flood fill de la coordonate (l, c)
// returneaza aria zonei din care se porneste fill (cite puncte 0)
int fill( int l, int c ) {
  int aria;

  lab[l][c] = 1;                   // marcam punctul curent ca vizitat
  aria = 1;                        // contorizam punctul curent
  if ( lab[l + 1][c] == 0 )        // daca nu este zid
    aria += fill(l + 1, c);        // cautam in jos
  if ( lab[l - 1][c] == 0 )        // daca nu este zid
    aria += fill(l - 1, c);        // cautam in sus
  if ( lab[l][c + 1] == 0 )        // daca nu este zid
    aria += fill(l, c + 1);        // cautam in dreapta
  if ( lab[l][c - 1] == 0 )        // daca nu este zid
    aria += fill(l, c - 1);        // cautam in stinga

  return aria;
}

int main() {
  FILE *fin, *fout;
  int n, l, c, ls, cs, a;

  fin = fopen( "arie.in", "r" );
  fscanf( fin, "%d%d%d ", &n, &ls, &cs );
  for ( l = 1; l <= n; l++ ) {
    for ( c = 1; c <= n; c++ )  // citim linia l a matricei
      lab[l][c] = fgetc( fin ) - '0';
    fgetc( fin ); // citim '\n'
  }
  fclose( fin );
  for ( c = 1; c <= n; c++ ) // bordare margini
    lab[0][c] = lab[n + 1][c] = lab[c][0] = lab[c][n + 1] = BORDER;

  a = fill( ls, cs ); // calcul arie accesibila din (ls, cs)
  
  fout = fopen( "arie.out", "w" );
  fprintf( fout, "%d\n", a );
  fclose( fout );

  return 0;
}

Număr goluri

Calcul număr de goluri: denumite și componente conexe, putem folosi fill pentru a număra cîte goluri disjuncte există (astfel încît să nu se poată ajunge de la un gol la altul). Pentru aceasta vom parcurge matricea în orice ordine și vom porni cîte un fill din fiecare loc unde găsim un element 0.

Iată un exemplu de program:

#include <stdio.h>

#define MAXN 1000
#define BORDER 2

char lab[MAXN + 2][MAXN + 2]; // matricea labirint

// Executa flood fill de la coordonate (l, c)
void fill( int l, int c ) {
  lab[l][c] = 1;            // marcam punctul curent ca vizitat
  if ( lab[l + 1][c] == 0 ) // daca nu este zid
    fill(l + 1, c);         // cautam in jos
  if ( lab[l - 1][c] == 0 ) // daca nu este zid
    fill(l - 1, c);         // cautam in sus
  if ( lab[l][c + 1] == 0 ) // daca nu este zid
    fill(l, c + 1);         // cautam in dreapta
  if ( lab[l][c - 1] == 0 ) // daca nu este zid
    fill(l, c - 1);         // cautam in stinga
}

int main() {
  FILE *fin, *fout;
  int n, l, c, ls, cs, nr;

  fin = fopen( "nrgol.in", "r" );
  fscanf( fin, "%d%d%d ", &n, &ls, &cs );
  for ( l = 1; l <= n; l++ ) {
    for ( c = 1; c <= n; c++ )  // citim linia l a matricei
      lab[l][c] = fgetc( fin ) - '0';
    fgetc( fin ); // citim '\n'
  }
  fclose( fin );
  for ( c = 1; c <= n; c++ ) // bordare margini
    lab[0][c] = lab[n + 1][c] = lab[c][0] = lab[c][n + 1] = BORDER;

  nr = 0;
  for ( l = 1; l <= n; l++ )
    for ( c = 1; c <= n; c++ ) // pentru fiecare punct din labirint
      if ( lab[l][c] == 0 ) {  // daca nu este zid si nu a fost umplut deja
        nr++;                  // contorizam un nou gol
        fill( l, c );          // umplem zona
      }
        
  fout = fopen( "nrgol.out", "w" );
  fprintf( fout, "%d\n", nr );
  fclose( fout );

  return 0;
}

Perimetru goluri

Calcul perimetru goluri: în locul ariei golurilor putem calcula perimetrul lor, anume numărul de puncte din goluri care se învecinează cu un punct care nu face parte din gol. Trebuie să avem grijă cînd testăm dacă un punct este pe perimetru.

Un punct se află pe perimetru dacă:

• Unul din vecinii săi este zid
• Sau unul din vecinii săi este margine bordată.

Un punct nu neapărat se află pe perimetru dacă:

• Unul din vecinii săi este un alt punct parcurs anterior

Cum ne dăm seama dacă vecinul este margine, zid, sau punct anterior? Vom umple golurile cu un număr distinct. În exemplul de mai jos marginile și zidurile sînt codificate cu 1 iar umplerea se face cu 2.

Iată un exemplu de program care afișează perimetrul golului accesibil din punctul inițial:

#include <stdio.h>

#define MAXN 1000
#define BORDER 1
#define FILL 2

char lab[MAXN + 2][MAXN + 2]; // matricea labirint

// Executa flood fill de la coordonate (l, c)
// returneaza perimetrul zonei din care se porneste fill (cite puncte 0)
int fill( int l, int c ) {
  int perimetrul;

  lab[l][c] = FILL;               // marcam punctul curent ca vizitat
  perimetrul = lab[l - 1][c] == 1 // verificam daca punctul curent este pe
    || lab[l + 1][c] == 1         // perimetru
    || lab[l][c - 1] == 1
    || lab[l][c + 1] == 1;        // daca da, contorizam punctul curent
  if ( lab[l + 1][c] == 0 )       // daca nu este zid
    perimetrul += fill(l + 1, c); // cautam in jos
  if ( lab[l - 1][c] == 0 )       // daca nu este zid
    perimetrul += fill(l - 1, c); // cautam in sus
  if ( lab[l][c + 1] == 0 )       // daca nu este zid
    perimetrul += fill(l, c + 1); // cautam in dreapta
  if ( lab[l][c - 1] == 0 )       // daca nu este zid
    perimetrul += fill(l, c - 1); // cautam in stinga

  return perimetrul;
}

int main() {
  FILE *fin, *fout;
  int n, l, c, ls, cs, p;

  fin = fopen( "perimetru.in", "r" );
  fscanf( fin, "%d%d%d ", &n, &ls, &cs );
  for ( l = 1; l <= n; l++ ) {
    for ( c = 1; c <= n; c++ )  // citim linia l a matricei
      lab[l][c] = fgetc( fin ) - '0';
    fgetc( fin ); // citim '\n'
  }
  fclose( fin );
  for ( c = 0; c < n; c++ ) // bordare margini
    lab[0][c] = lab[n + 1][c] = lab[c][0] = lab[c][n + 1] = BORDER;

  p = fill( ls, cs ); // calcul perimetru accesibil din (ls, cs)
  
  fout = fopen( "perimetru.out", "w" );
  fprintf( fout, "%d\n", p );
  fclose( fout );

  return 0;
}

Eliminare zid

Ne propunem să eliminăm acea pătrațică zid care reduce la minim numărul de goluri.

Cum procedăm?

Soluție forță brută: o soluție forță brută ar fi să eliminăm pe rînd fiecare bucată de zid și să numărăm golurile formate.

Ce complexitate are această soluție?

Deoarece numărul de ziduri poate fi O(n²) iar numărarea golurilor este și ea tot O(n²) rezultă o complexitate de O(n⁴).

Se poate mai bine? Desigur.

Soluție optimă: soluția optimă este similară cu cea care numără golurile:

• Umplem toate golurile.
• La fiecare gol umplem cu o valoare diferită de fill.
• La final parcurgem matricea căutînd pătrățica zid care are ca vecini cele mai multe goluri diferite (eticheta diferită).

Ce complexitate are această soluție?

• Umplerea golurilor este O(n²).
• Verificarea zidurilor este O(n²).

Timpul total va fi, deci, O(n²).

Concluzie

Fill este o unealtă simplă și utilă, ușor de folosit la concursuri. Principalul ei neajuns este memoria ocupată. Ce facem în situația cînd matricea este prea mare și memoria disponibilă insuficientă pentru a folosi flood fill? În această situație putem folosi BFS fill (breadth first search), care, atunci cînd este aplicat pe o matrice se mai numește și algoritmul Lee. El folosește o coadă pentru a menține frontiera deja acoperită, reducînd memoria la O(m+n) însă fiind ceva mai lent. Vom discuta acest algoritm într-o altă lecție.

Temă

• Tema 10 clasa a 7^a
  • oraș dată la .campion 2011
  • enclave de exercițiu în flood fill

• Tema 10 opțională clasa a 7^a
  • ozn dată la barajul pentru Shumen din Tudor Vianu anul 2014, juniori

Rezolvări aici [2]