Fulgerică - rezolvare

Problema cere să se determine dacă un milion de numere de la intrare pot forma o suită.

Comentarii

Corectînd lucrările voastre am aflat lucruri surprinzătoare despre voi. Cei cărora li se aplică observațiile de mai jos, atenție: sunt semne de IQ coborît. Ceea ce poate constitui o problemă în cadrul unei școli care se cheamă 'IQ Academy'.

Cînd v-am spus să scrieți ce vreți și cum vreți, doar să înțeleg algoritmul, nu mă așteptam la o surpriză neplăcută: mulți dintre voi aveți un scris dezlînat, dezordonat, cu greșeli gramaticale. Scrieți cu litere de o șchioapă (mari pentru cei ce nu știu ce înseamnă). Nu aveți o aliniere, deși paginile erau liniate. Două apariții ale aceleiași litere nu seamănă. Nu zice nimeni să scrieți frumos, dar scrisul vostru este de om care nu scrie niciodată, nu și-a creat încă obișnuița de a desena literele. Arată a scris de om prost sau cu probleme mentale.
Cei care mi-ați scris romane pe patru pagini, v-ați gîndit că ar fi fost util să le numerotați? A trebuit să fac inginerie inversă să mă prind care este capul și care este coada aiurelii pe care ați scris-o, care, pe lîngă că nu avea sens, nici nu era în ordine.
Unii din voi ați scris pe o dublă foaie, pliată, luată de la mijlocul caietului. Bun. Dar unii ați început să scrieți pe ultima foaie! O dezordine greu de imaginat, doar dacă nu cumva v-ați închipuit că scrieți în ebraică. Genul ăsta de dezordine maximală nu cadrează cu informatica.
Problema era de clasa a cincea, cel mult a șasea. Era banală. Cu toate acestea doar 7 din 36 au dat un algoritm rezonabil. Ceilalți 29? Să vă fie rușine.
Mulți dintre voi nu și-au dat seama că nu puteți încărca numerele în memoria dată. La clasa a șaptea nu știți să vă calculați memoria. Unul din voi a scris "creăm un vector de frecvență de 10¹⁸ numere". Apoi a tăiat.

Clasament

Nr.	Nume	F1
1	Iordache	100
1	Ipate	100
1	Petrescu	100
1	Voicu M	100
5	Dobre	95
6	Tatomir	90
7	Ghica	85
8	Ruginiș	15
9	Badea	10
9	Rebengiuc	10
11	Petcu	5
11	Marcu	5
13	Aizic	0
13	Asgari	0
13	Benescu	0
13	Burac	0
13	Cadîr	0
13	Calotă	0
13	Chivu	0
13	Cojocariu	0
13	Dimulescu	0
13	Fares	0
13	Grecu	0
13	Hossu	0
13	Ilie	0
13	Mocanu	0
13	Moroșan	0
13	Mușat	0
13	Nicola	0
13	Nicu	0
13	Popescu	0
13	Stancu	0
13	Ștefănescu	0
13	Teodorescu	0
13	Togan	0
13	Voicu T	0

Tema - rezolvări

Cuburi

Problema cuburi a fost dată la ONI 2012 clasa a 8^a.

Comentarii generale

Avertismente lui: Fares (nici o sursă)

Maxim

O variantă simplificată a problemei maxim a fost dată la ONI 2007 clasa a 5^a.

Comentarii generale

Puțini ați încercat o soluție O(Σ) :-( Nu vă plac provocările?
O coadă are lungime putere a lui doi pentru a nu face împarțiri. Dacă indicii nu ajung vreodată să treacă peste maxim, circular, nu are sens să declarăm coada de lungime putere a lui doi. Nu facem decît să mărim memoria alocată.
Majoritatea dintre voi ați declarat coada astfel încît să încapă toate cifrele. Caz în care nu avem nevoie de circularitate.
Cum trebuia să procedați, corect? Trebuia să executați programul pe maxim, cu a=1 și b=10000 și să vedeți cît necesită în realitate coada.
Sau, și mai bine, să vă dați seama că coada este o înșiruire de maxime ce pot avea maxim zece valori (cifre) și să o țineți minte ca o coadă de perechi (cifră, nr. apariții).

Comentarii individuale

Prima grupă

Badea: Ai comentarii utile, bravo! Nu folosești debugerul ci printf, bravo! Greșeala constă în cum memorezi poziția: în algoritmul din curs ea este poziția din fereastră. Tu ai folosit poziția absolută. Ai declarat toți vectorii de QMAX. Coada e bine să aibă putere a lui 2, dar vectorii nu. Coada este atît de mare încît nu este circulară: încap toate cifrele în ea. Trebuia să măsori cît ai nevoie.
Calotă: program bun. Folosești o coadă dublă, dar în ea încap toate cifrele, nu va fi niciodată circulară. Se poate ceva mai simplu și cu mai puțină memorie, vezi soluția mai jos.
Dobre: Program relativ simplu si clar. Nu folosești coadă dublă, acesta era scopul temei. Niște comentarii ar fi ajutat enorm. Gen: "aici generez cifrele numărului x în ordine inversă". Apoi "aici inversez vectorul de cifre". În particular, asta e inutil, puteai să îl folosești direct, nu? Folosești fprintf pentru a tipări cifre, risipitor și lent! Trebuia să folosești fputc.
Hossu: Calcule greșite, numărul de cifre poate fi mai mare, cel puțin pentru vectorul v[] unde stochezi cifrele numărului maximal. Ai făcut parsing pentru citirea a trei numere. Are sens? Stochezi cifrele numărului adunînd la ele '0'. Faci confuzie între întregul 0 pe tipul char și caracterul '0'. Greșeală de clasa a cincea, care îți complică inutil codul. Ai o variabilă flag care este, de fapt, un contor. Ai un avertisment de compilare care pare grav. În general, codul tău nu are prea mult sens.
Mocanu: Programul este bun ca algoritm. Implementarea este destul de încîlcită și cu repetiție de cod. Cred că îl poți depana, ai acum testele. Cred, de exemplu, că felul cum aduci la zi k este greșit, trebuia să scazi cu unu în minus. Mulțumesc pentru comentarii, ajută mult! Niciodată să nu scrii while(v[s[j]]<v[i] && j>=0). Poți depăși memoria. Inversează cele două condiții: while(j>=0 && v[s[j]]<v[i]). for(a=a;a<=b;a++) se scrie mai simplu for(;a<=b;a++). De ce folosești vectorul v[] de cifre de la unu și nu de la zero?
Mușat: Coada programului tău va conține toate cifrele, deci nu va fi niciodată circulară. Programul tău, deși fără comentarii, este, din fericire, bine structurat și împărțit astfel încît am putut să-i urmăresc logica. Este aproape perfect. Ratezi teste pentru că ajustezi greșit k, trebuia să mai scazi unu.
Togan: Programul pare că are sens, ai indici de prim și ultim, menții o structură de maxime. Dar cam atît. Ai zero comentarii, mi-e greu să îmi dau seama ce faci. Și clar faci prostii, nu folosești o coadă dublă. Acesta era scopul temei. Duplici mult cod. Nu folosești constante. Pui pe zero elementele eliminate din coadă, de ce?

A doua grupă

Nicu: Algoritmul arată bine. Implementarea nu, repeți mult cod. Coada ta e atît de mare încît încap toate cifrele în ea. Deci nu va fi niciodată circulară, toate operațiile modulo sînt inutile. Folosește constante! Este inacceptabil să ai același număr de zece ori în program.
Rebengiuc: program perfect, bravo! Folosești memorie O(Σ), iar programul este simplu, clar, fără repetiții de cod și cu comentarii. Vezi o mică modificare în soluția de mai jos: putem merge cu cifrele pînă la finalul cifrelor chiar în bucla principală, cu condiția ca mai întîi să adăugăm și apoi să scoatem maximul. Cînd coada devine goală vom adăuga și scoate aceeași cifră mereu.
Rughiniș: Nu ai stocat vectorul de cifre, bravo! Ți-ai calculat memoria necesară, bravo! Dar nu ai calculat memoria strict necesară, poate puteai să o mai reduci folosind o coadă circulară. Comentarii bune, bravo! Ai repetiție de cod seminificativă. Cred că pici teste deoarece ai o gestiune greoaie a cifrelor de la intrare. Mai exact, cred ca testul a <= b folosit de (prea) multe ori în program nu este tocmai corect în toate pozițiile.
Stancu: Programul are sens. Nu este deloc ceva standard, drept care m-ar fi ajutat sa pui comentarii. Nu folosești o coadă dublă, acesta era scopul temei. Ai avertisment serios de compilare, sper că te-ai uitat pe el. Nu scrie niciodată while( v[i] > deque[vf] && vf >= 0 ). Este o greșeală de clasa a cincea, care poate duce la depășirea memoriei, signal 11. Totdeauna scrie invers: while( vf >= 0 && v[i] > deque[vf] ). Faci de asemenea o treabă ne-OK: transferi toate elementele cozii spre stînga cu o poziție. Aceasta distruge complexitatea algoritmului, el devenind O(N²).

JBird

Problema jbird este o problemă-exercițiu de implementare a maximului în fereastră glisantă.

Comentarii generale

Unii din voi, destul de mulți, nu ați făcut parsing, sau ați făcut doar parsing-ul intrării. Conform discuțiilor, pentru a nu risca, era bine să le faceți pe ambele. Gîndiți și calculați!
Avertismente lui: Ghica (nici o sursă)

Comentarii individuale

Prima grupă

Badea: Program bun, bravo! Păcat că nu ți-a ieșit în concurs. Ai făcut parsing la intrare, bravo! De ce nu și la ieșire? Faci popfront și, dacă nu era nevoie, faci la loc pushfront. Cam risipitor, puteai fie să citești direct primul număr din coadă, fie să folosești o altă funcție, peekfront.
Calotă: Algoritm bun, implementare defectuoasă. Coada are mărimea de maxim 2K+1. Tu ai declarat-o de N+2K+1. Risipă uriașă. Ai cam mulți vectori, vectorul original, vectorul de răspunsuri, coada și toate declarate risipitor, prea mari. N-ai făcut parsing, îți place să trăiești periculos.
Dobre: program lung, fără nici un comentariu. Greu de urmărit, mult cod duplicat. Voi face doar comentarii superficiale. Setezi la zero pozițiile din coada unde elimini elemente, de ce? Este inutil. Folosești o santinelă. Acest lucru nu este posibil într-o coadă, vei pierde timp mutînd santinela, iar codul devine mai complicat. Cea mai mare problemă a codului este duplicarea masivă. Acest lucru îl face greu de urmărit și greu de depanat. Este un cod sortit să ia scor mic.
Hossu: Algoritmul este bun, bravo. Ai făcut parsing atît al intrării cît și al ieșirii, bravo! În coada ta încap toate înălțimile, deci nu e o coadă, căci nu va merge niciodată circular. Ai o depășire gravă de memorie cînd scrii m[i - k] = coada[prim]; Nu testezi că i >= k. Ai un noroc formidabil :)
Mocanu: Comentariul inițial este extrem de folositor, bravo! Altfel nu aș fi înțeles de ce ai atîția vectori. Problema e că nu îți încap în memorie. Sper că ai calculat cîtă memorie ocupi. Programul arată rezonabil. Dar repeți enorm de mult cod, nu ai voie la astfel de programe, altfel ele vor fi foarte greu de depanat. Nu reușesc să mă descurc în el.
Mușat: Algoritm bun, bravo! Faci parsing la intrare, bun! De ce nu și la ieșire? Am văzut că l-ai scris încă din timpul concursului. Sper că este doar al tău, fără ajutoare.
Togan: Algoritm simpatic, care calculează maximul în ferestre de K+1 și apoi folosește cîte două ferestre pentru a calcula maximul cerut. Setezi la zero pozițiile din coadă unde elimini elemente, total inutil. Felul în care testezi maximele din cele două ferestre este foarte încîlcit. Era deajuns să calculezi poziția maximelor în vector și să ajustezi, pe rînd, cele două poziții pentru a le aduce în vector. Poate era mai simplu să calculezi direct maximul în ferestre de 2K+1. Repeți cod destul de mult. Zero comentarii, îmi faci viața foarte grea.

A doua grupă

Nicu: Program bun, bravo! Repeți mult cod. Folosește constante, codul este ridicol cu numere peste tot! Nu faci parsing, îți place să trăiești periculos! :-)
Rughiniș: program foarte bun, bravo! Folosești minim de memorie, bravo! Nu parsezi intrarea/ieșirea. Îți place să trăiești periculos! :-)
Rebengiuc: program foarte bun! Bravo! Ai făcut parsing atît la intrare cît și la ieșire, frumos. Ai folosit minimul de memorie posibil, bravo!
Stancu: programul e o prostie, forță brută, nu acesta era scopul temei. Nu ai exersat coada dublă.

Rezolvări aici [1]

Lecţie

<html5media height="720" width="1280">https://www.algopedia.ro/video/2019-2020/2020-01-23-clasa-7-lectie-info-18-720p.mp4</html5media> Să studiem următoarea problemă:

Problema disjoint

Problema disjoint:

Se dau N mulţimi de numere, iniţial fiecare mulţime i conţinând un singur element, mai exact elementul i. Asupra acestor mulţimi se pot face 2 tipuri de operaţii, astfel:

operaţia de tipul 1: se dau două numere naturale x si y, între 1 şi N. Se cere să se reunească mulţimile în care se află elementul x, respectiv elementul y (se garantează că x şi y nu se vor afla în aceeaşi mulţime)
operaţia de tipul 2: se dau două numere naturale x şi y, între 1 şi N. Se cere să se afişeze DA dacă cele 2 elemente se află în aceeaşi mulţime, respectiv NU în caz contrar.

Date de intrare

Pe prima linie a fişierului de intrare disjoint.in se vor afla 2 numere, N şi M, reprezentând numărul de mulţimi, respectiv numărul de operaţii efectuate. Pe următoarele M linii se vor afla câte 3 numere, cod, x şi y, cod reprezentând tipul operaţiei, iar x şi y având semnificaţia din enunţ.

Date de ieşire

În fişierul de ieşire disjoint.out se vor afişa mai multe linii, fiecare linie conţinând DA sau NU, reprezentând răspunsul la interogarea corespunzătoare din fişierul de intrare.

Restricţii

1 ≤ N ≤ 100 000
1 ≤ M ≤ 100 000

Exemplu

`disjoint.in`	`disjoint.out`
`4 6 1 1 2 1 3 4 2 1 3 2 1 2 1 1 3 2 1 4`	`NU DA DA`

Algoritmul union-find

Problema disjoint şi rezolvarea ei, este o unealtă foarte utilă din trusa de scule a algoritmistului. Să definim problema:

Dată o mulţime A de valori de la 0 la N-1 definim submulţimi disjuncte pe această mulţime, astfel încît aceste submulţimi să acopere mulţimea originală A. Apoi începem să reunim unele dintre aceste mulţimi. Reuniunea se face menţionînd două elemente ale submulţimilor ce se doresc reunite (dacă elementele se găsesc deja în aceeaşi submulţime nu vom face nimic). După ce efectuăm aceste operaţii de reuniune dorim să răspundem la întrebarea 'ce submulţimi avem?'.

Cu alte cuvinte, cunoscînd N şi ştiind că iniţial fiecare număr face parte din propria submulţime şi apoi dîndu-se mai multe perechi de numere (a_i, a_j) cu semnificaţia "mulţimea din care face parte a_i se reuneşte cu mulţimea din care face parte a_j" trebuie ca în final să spunem ce submulţimi există.

Pentru a implementa algoritmul vom avea nevoie de două operaţii:

reuneşte două mulţimi (union)
găseşte mulţimea unui element (find)

De aici şi denumirea problemei union-find. În română se regăseşte sub numele de colecţie de mulţimi disjuncte, dar denumirea de union-find tinde să fie mai folosită în cercurile de algoritmişti.

Soluție forță brută

O soluție posibilă ar fi ca pentru fiecare număr i să memorăm mulțimea din care face el parte. Astfel, m[i] va conține numărul mulțimii lui i. Dacă i și j fac parate din aceeași mulțime atunci m[i] = m[j], în caz contrar m[i] ≠ m[j].

Inițial fiecare număr va avea propria lui mulțime, adică m[i] = i.

Operația Find

Precum am spus, find(i) ne va da un identificator unic al mulțimii elementului i. În cazul nostru el va fi un număr între 0 și N-1. Cum o implementăm? Returnînd chiar m[i]!

int find( int i ) {
  return m[i];
}

Ce complexitate are această operație?

Desigur O(1).

Operația Union

Operația union(i, j) trebuie să reunească mulțimile din care fac parte elementele i, respectiv j. Cum o implementăm? Suprascriind identificatorul mulțimii lui j cu identificatorul mulțimii lui i, peste tot unde apare el.

void union( int i, int j ) {
  int k, mj = m[j];

  for ( k = 0; k < N; k++ )
    if ( m[k] == mj )
      m[k] = m[i];
}

Ce complexitate are această operație?

Desigur O(N).

Concluzie

Cu forța brută vom avea complexitățile:

Find: O(1) timp
Union: O(N) timp
Memorie necesară: O(N)

Soluție alternativă

Să încercăm să optimizăm operația union. Actualizarea identificatorilor mulțimii durează mult. Ce putem face?

O idee ar fi ca, în loc să actualizăm toți identificatorii mulțimii lui j, să îl actualizăm doar pe al lui j. Astfel, fiecare element între 0 și N-1 va ţine mine un şef al său din mulţime. Întocmai ca într-o companie, fiecare element al unei submulţimi va raporta unui şef, şefii vor raporta altor şefi şi aşa mai departe pînă ce se ajunge la şeful unic, conducătorul submulţimii. El nu are şef şi este considerat reprezentantul acelei submulţimi.

Cum memorăm acest lucru? Printr-un simplu vector de şefi (similar vectorului m[]) în care elementul sef[i] este numărul din mulţimea 0..N-1 care este şeful lui i. Ce punem în elementele şefi supremi, cele care nu au șefi? Pentru a le distinge de elementele subalterni fiecare şef suprem este propriul lui şef. Dacă elementul i este şef suprem atunci sef[i] = i. O alternativă la această reprezentare, dacă "sacrificăm" elementul 0, este să memorăm zero ca şef fictiv pentru elementele reprezentative ale mulţimilor.

Inițial fiecare element este propriul său șef. Atunci cînd căutăm o mulțime, căutăm de fapt șeful suprem, care este propriul său șef. Cînd unificăm mulțimile lui i și ale lui j vom nota că șeful mulțimii i devine șeful șefului mulțimii j.

Operația Find

Precum am spus, find(i) va returna șeful mulțimii din care face parte i. Cum îl găsim? Mergînd la șeful lui i, apoi la șeful șefului lui i și tot așa pînă la șeful mulțimii. Iată o implementare recursivă simplă:

int find( int i ) {
  if ( sef[i] == i )     // daca am gasit seful suprem
    return i;            // il returnam
  return find( sef[i] ); // altfel returnam seful sefului
}

Ce complexitate are această operație?

Care este cazul cel mai rău? Cînd toate elementele se înșiră într-un lanț lung de șefi. În acest caz timpul este O(N).

Operația Union

Operația union(i, j) trebuie să reunească mulțimile din care fac parte elementele i, respectiv j. Cum o implementăm? Suprascriind identificatorul mulțimii lui j cu identificatorul mulțimii lui i, peste tot unde apare el.

void union( int i, int j ) {
  int sefi, sefj;

  sefi = find( i ); // seful suprem al lui i
  sefj = find( j ); // seful suprem al lui j

  sef[sefj] = sefi; // seful suprem al lui sefj devine sefi
}

Ce complexitate are această operație?

Ea apelează de două ori find(), iar apoi face O(1) operații.

Concluzie

Cu soluția alternativă avem complexitățile:

Find: O(N) timp
Union: O(1) timp + complexitatea lui Find
Memorie necesară: O(N)

Nu pare că am avansat, nu? Poate că nu. Observăm, însă, că timpul total depinde de Find: dacă reușim să îmbunătățim complexitatea lui Find automat vom îmbunătăți și complexitatea lui Union.

Putem îmbunătăți timpul lui find la O(log N) cu o modificare destul de mică a structurii de date, dar nu voi prezenta acest lucru. Pentru cei curioși, putem memora cea mai lungă cale de șefi din fiecare mulțime, iar apoi vom atașa mulțimea mai mică la cea mai mare (alegînd în mod potrivit dacă atașăm șeful lui i la j sau invers).

Soluție eficientă folosind compresia căii

Pentru a obţine cel mai eficient algoritm cunoscut avem nevoie de două optimizări: compresia căii și menținerea unui rang al fiecărei mulțimi. Voi prezenta aici doar una dintre ele, cea mai importantă, compresia căii. Ea face un lucru foarte simplu: schimbă puţin funcţia find ca, atunci cînd dorim să aflăm care este şeful nodului i, să lege toţi şefii parcurşi direct la şeful suprem. Cu alte cuvinte vom parcurge aceiaşi şefi intermediari pînă la şeful suprem, dar odată găsit va trebui să ne întoarcem la şefii intermediari şi să le schimbăm şeful. Aceasta duce aproximativ la o dublare a opreaţiilor efectuate de find. Dar, precum spunea astronatul Neil Armstrong, un pas mic pentru un om poate fi un pas uriaş pentru omenire. O mică modificare ce duce la dublarea timpului lui find duce la o scurtare fantastică a următoarelor operaţiuni find.

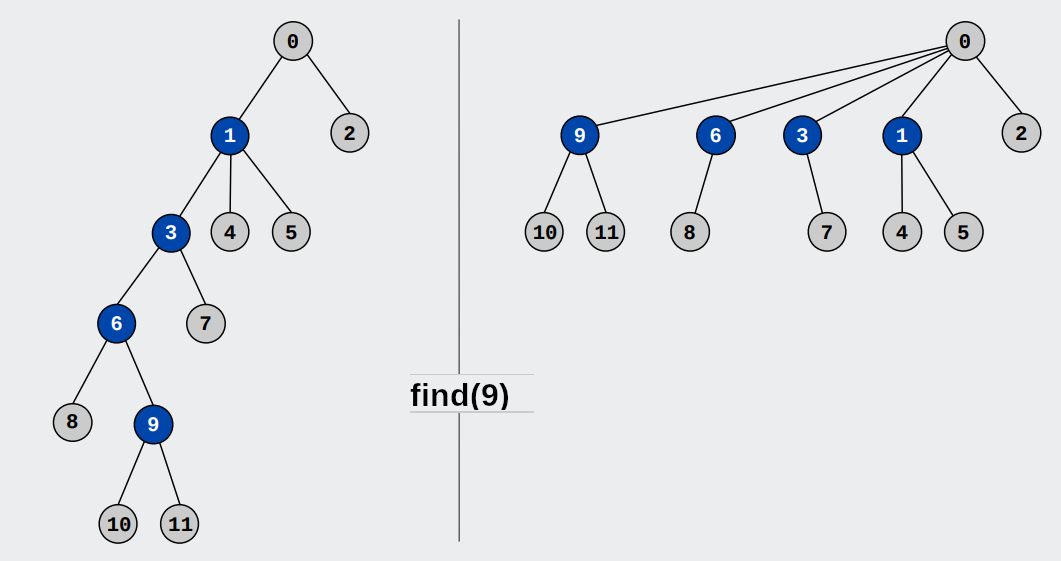
Această optimizare poartă denumirea de compresia căii, sau, în engleză, path compression.

Operația Find

Iată o modificare mică a funcției anterioare, care face și compresia căii:

int find( int i ) {
  if ( sef[i] == i )   // daca am gasit seful suprem
    return i;          // il returnam
  return sef[i] = find( sef[i] ); // altfel legam i la seful suprem, pe care il si returnam
}

Operația Union

Operația union(i, j) trebuie să reunească mulțimile din care fac parte elementele i, respectiv j. Cum o implementăm? Suprascriind identificatorul mulțimii lui j cu identificatorul mulțimii lui i, peste tot unde apare el.

void union( int i, int j ) {
  int sefi, sefj;

  sefi = find( i ); // seful suprem al lui i
  sefj = find( j ); // seful suprem al lui j

  sef[sefj] = sefi; // seful suprem al lui sefj devine sefi
}

Ce complexitate au aceste operații?

În această implementare, ele sînt O(log N) amortizat, per operație, cu o constantă foarte mică. Demonstrația acestui lucru depășește cadrul acestui curs.

Concluzie

Cu compresia căii avem complexitățile:

Find: O(log N) timp
Union: O(log N) timp
Memorie necesară: O(N)

Notă: se poate mai bine. Dacă adăugăm și cealaltă optimizare menționată mai sus, rangul unei mulțimi, ajungem la o complexitate O(α(N)), unde α(N) este inversul funcției lui Ackermann, o funcție rapid crescătoare. Cu această modificare timpul amortizat este, practic, constant.

Inversarea sensului

Ocazional veți întâlni problema inversă: se pornește cu o structură conexă care, treptat, este deconectată. Pe parcurs, se cer informații despre conexitate. Aceasta este o problemă de partiționare, care nu admite o soluție directă la fel de simplă.

Dar, când memoria permite stocarea șirului de operații, o soluție este:

Executăm toate operațiile de deconectare, obținând structura finală.
Executăm în ordine inversă operațiile, care acum reconectează structura. Putem face aceste operații cu structuri de mulțimi disjuncte.
Notăm răspunsurile la interogările de conexitate.
Tipărim aceste răspunsuri în ordine inversă.

Exemplu: bile3, ruine.

Fulgerică (test fulger)

Găsiți un algoritm la următoarea problemă și explicați-l pe o foaie de hîrtie. Dacă nu vă descurcați să îl explicați puteți scrie cod. Sau formule matematice. Sau puteți scrie din toate trei. Important este ca algoritmul să se înțeleagă și să fie corect. Atenție! Spre deosebire de varena, vi se cere un algoritm corect, echivalentul unei rezolvări care să treacă toate testele. Nu gîndiți la modul "cum fac să iau cît mai multe puncte". Nu se acceptă "mînăreli". Voi corecta lucrările personal. Nu vă concentrați pe citire, sau scriere.

Problema mulțime

Se dau la intrare un milion de numere între 0 și 10¹⁸. Să se spună dacă mulțimea acelor elemente conține maxim 1000 de numere. Cu alte cuvinte, dacă am elimina duplicatele dintre cele un milion de numere, am rămîne cu cel mult 1000 de numere. De exemplu, dacă la intrare avem numerele 1 5 3 4 2 5 3 1 3, după ce eliminăm duplicatele rămînem cu 5 numere: 1 5 3 4 2, deci răspunsul va fi 'DA'. La ieșire veți afișa 0 dacă rămîn mai mult de 1000 de numere, sau 1 în caz că rămîn cel mult 1000 de numere.

Restricţii

timp de execuție: o secundă sau două.
memorie disponibilă: 8KB și oricîte variabile simple.

Temă

Tema 18 clasa a 7^a
- disjoint
- channels
- bile3
Opţional: Tema 18 clasa a 7^a opţională
- flota
- ruine

Rezolvări aici [2]

Clasa a VII-a lecția 18 - 23 ian 2020

Fulgerică - rezolvare

Comentarii

Clasament

Tema - rezolvări

Cuburi

Comentarii generale

Maxim

Comentarii generale

Comentarii individuale

Prima grupă

A doua grupă

JBird

Comentarii generale

Comentarii individuale

Prima grupă

A doua grupă

Lecţie

Problema disjoint

Date de intrare

Date de ieşire

Restricţii

Exemplu

Algoritmul union-find

Soluție forță brută

Operația Find

Operația Union

Concluzie

Soluție alternativă

Operația Find

Operația Union

Concluzie

Soluție eficientă folosind compresia căii

Operația Find

Operația Union

Concluzie

Inversarea sensului

Fulgerică (test fulger)

Problema mulțime

Restricţii

Temă

Navigation menu

Search