Clasa a VII-a lecția 2 - 26 sep 2019

Anunțuri

• Nu îmi este clar de ce unii dintre voi (în special cei de la Vianu) au trimis soluții la problema selecție. Pînă aici nu este o problemă. Ce nu înțeleg este de ce ați folosit C++ și, mai ales, de ce ați folosit o funcție de bibliotecă pentru a o rezolva. Dacă vreți să fiți simpli utilizatori nu aveți nevoie de IQ Academy pentru aceasta.
• Sînteți clasa a șaptea (mulți dintre voi :-). Acum este momentul să scrieți programe scurte și eficiente. Faceți efortul să scăpați de obiceiurile proaste: duplicare de cod, stegulețe inutile, gîndire încîlcită. Dacă faceți asta acum veți avea o viață mult mai ușoară ca informaticieni. Dacă nu faceți asta acum vă va fi foarte greu (iar unora imposibil) să vă corectați în viitor.
• Știți funcții. Pe unii dintre voi îi ardeau degetele să le folosiți. Iar acum, cînd are și sens, nu le folosiți? Majoritatea ați repetat codul de calcul la problema magic.

Tema - rezolvări

Rezolvări aici [1]

Lecție

<html5media height="720" width="1280">https://www.algopedia.ro/video/2019-2020/2019-09-26-clasa-7-lectie-info-02-720p.mp4</html5media>

Problema selecției

Dat un șir de n numere și o poziție k în acel șir să se spună ce element s-ar afla pe acea poziție dacă șirul ar fi sortat.

Exemplu

Fie șirul 3 9 23 13 18 8 3 10 2 10 15 21 și poziția k = 6

Dacă am ordona șirul am obține 2 3 3 8 9 10 10 13 15 18 21 23. Pe poziția 6 se află elementul 10, care este și răspunsul dorit.

Soluție forță brută

O soluție ce vine ușor în minte este să sortăm vectorul și apoi să afișăm elementul de la poziția k. Nu este eficientă, complexitatea ei va fi O(n²) cu sortare prin selecție, sau O(n log n) cu sortări mai rapide.

Quick select

Aplicăm un pas de pivotare în mod repetat. Algoritmul este prezentat aici: quickselect.

Ideea pivotării este următoarea: alegem un așa numit pivot. El este un element oarecare din vector. Putem să alegem elementul aflat la jumatea vectorului, v[n / 2]. Sau putem să îl alegem la întîmplare, folosind o funcție ce generează numere aleatoare, cum ar fi funcția rand() în C (parte din biblioteca stdlib.h). Fie p indicele pivotului și val = v[p] valoarea acelui pivot. Ne propunem să separăm vectorul în două: prima parte va conține elemente mai mici sau egale cu pivotul val. A doua parte va conține elemente mai mari sau egale cu pivotul val.

Odată efecutată pivotarea vom ști în care din cele două părți se va afla elementul pe poziția k în vectorul sortat. Putem, deci, selecta acea parte, continuînd algoritmul doar pentru acel subvector.

Există mai mulți algoritmi de pivotare, toți liniari. Vă rămîne ca temă să vă gîndiți la algoritm și să îl implementați. Puteți să căutați pe net, ideal ar fi să îl gîndiți voi singuri. Dacă totuși nu vă descurcați v-aș recomanda să implementați algoritmul original al lui Tony Hoare. Atenție! El nu este structurat! Va trebui să îl modificați!

Ce complexitate are acest algoritm?

Vom aplica în mod repetat pivotarea, ce are complexitate O(n). Pe medie vom păstra, la fiecare pas, jumătate din vector. Complexitatea va fi, deci, O(n + n/2 + n/4 + ... + 1). Observăm că suma nu va depăși niciodată 2n (deși se va apropia de acea valoare). Complexitatea este, deci O(n).

Atenție! Aceasta este o complexitate medie! Pe cazul cel mai rău putem să selectăm mereu o parte a vectorului care are cu un element mai puțin ca vectorul curent, ceea ce duce la o complexitate de O(n²) pe cazul cel mai rău.

Aplicăm repetat pivotarea quicksort. Calcul aproximativ al complexității pe cazul mediu: este O(n), în loc de O(n log n) dacă am fi făcut sortare.

Una din problemele de la temă vă cere să implementați acest algoritm. Vă rog nu trișați, nu apelați nth_element() (care oricum este C++, nu C).

Medianul medianelor

Acest algoritm îmbunătățește quickselect aducîndu-l la o complexitate liniară pe cazul cel mai rău. Depășește cadrul acestui curs, drept care nu îl voi prezenta. Pentru curioși, el este prezentat aici: medianul medianelor.

Stive

Stiva (în engleză stack) este un concept simplu, pe care l-am mai folosit în trecut, fără a sublinia faptul că folosim o stivă. O stivă este o "grămadă" de obiecte ordonate după ordinea LIFO: last in, first out. Aceasta înseamnă că putem adăuga obiecte în stivă, iar atunci cînd le vom scoate, le vom scoate în ordine inversă față de cum le-am adăugat. Vom vedea în lecțiile următoare că, prin contrast, coada scoate obiectele în aceeași ordine în care au fost adăugate.

Merită să spunem aici două vorbe despre tipuri de date abstracte.

Tip de date abstract

Un tip de date abstract este un model matematic, ce privește tipul de date din punctul de vedere al utilizatorului. Astfel, el definește operații asupra datelor și comportamentul acestor operații, dar nu specifică o implementare.

Tipurile de date abstracte separă funcționalitatea de implementare. Acest lucru este util pentru analiza complexității algoritmilor. Este de menționat faptul că unele TDA au multiple implementări, cu avantaje și dezavantaje, precum vom vedea în lecțiile următoare.

Stiva este un tip de date abstract în care definim operațiile:

• push(value) - inserează o valoare dată la sfârșitul listei;
• top - returnează valoarea de la sfârșitul listei;
• pop - șterge valoarea de la sfârșitul listei.
• empty - returnează 1 dacă stiva este goală (poate fi implementată și în cadrul operației top)

Pentru aceste operații există restricția menționată, anume că valorile trebuie returnate cu regula LIFO.

Implementare: stivă de întregi pozitivi sau zero

În practică stiva se implementează aproape întotdeauna ca un vector căruia i se adaugă la coadă elemente:

#define MAXN 1000

int stack[MAXN];       // stocarea valorilor propriu-zise
int stack_pointer = 0; // indice la prima valoare nefolosita in vector (totuna cu numărul de elemente din stiva)

// adauga valoarea 'val' la stiva, daca aceasta nu este plina
// returneaza 1 in caz de succes, 0 in caz de stiva plina
int push( int val ) {
  if ( stack_pointer >= MAXN )  // stiva este plina?
    return 0;                   // returnam eroare

  stack[stack_pointer++] = val; // adaugam valoarea in stiva
  return 1;                     // returnam succes
}

// returnează valoarea aflată în virful stivei, dacă ea exista
// in caz contrar returneaza -1
int top() {
  return stack_pointer > 0 ? stack[stack_pointer - 1] : -1;
}

// elimina ultimul element din stiva daca se poate
// returneaza 1 daca operatia a reusit, 0 in caz de eroare
int pop() {
  if ( stack_pointer == 0 ) // testam cazul de eroare
    return 0;

  stack_pointer--; // daca avem elemente pe stiva, il eliminam pe ultimul
  return 1;
}

// returneaza 1 daca stiva este goala, 0 in caz contrar
int empty() {
  return stack_pointer > 0;
}

Observații:

• În această implementare cele patru operații au complexitate O(1).
• Remarcați o folosire corectă a funcțiilor: ele implementează operațiuni ce au sens separat, de sine stătător.
• Remarcați denumirile funcțiilor: ele sugerează operațiunea implementată.
• Am folosit instrucțiunea return în mijlocul funcției. Aceasta este o excepție de la regulă. Pe caz general, atunci cînd la intrarea într-o funcție avem de tratat cazuri particulare de ieșire imediată din funcție, putem folosi instrucțiunea return. Codul devine astfel mai clar, iar restul corpului funcției nu se deplasează spre dreapta prin indentare.

Probleme ce necesită tipul stivă, date la concursuri

Exemple de probleme ce folosesc stive în rezolvări:

• bile2 dată la concursul .campion 2005
• turn dată la ONI 2007 clasa a 6^a
• paranteze1 dată ca temă la cercul IQ Academy 2018 clasa a 6^a
• swap dată la ONI 2013 baraj gimnaziu

Liste

Definiție

Definiție: în informatică o listă înlănțuită este o structură de date care constă dintr-un grup de noduri care împreună reprezintă o secvență. În forma ei cea mai simplă fiecare nod este format din date și o referință (înlănțuire) către nodul următor în secvență. Lista înlănțuită permite inserarea și ștergerea eficientă a elementelor de pe orice poziție în secvență.

Exemplu de listă înlănțuită

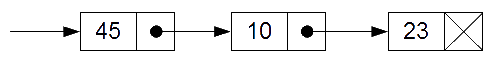
Implementare

O implementare posibilă este folosind doi vectori: un vector v[] care memorează elementele listei (numere întregi de exemplu) și un vector next[], care memorează indicele următorului element din listă. Perechea (v[i], next[i]) conține o celulă sau un nod al listei. Această celulă este memorată la poziția i, dar ea nu este celula numărul i! Ordinea în care memorăm celulele listei în vector nu are nici o relevanță. Importantă este înlănțuirea acestor celule, dată de vectorul next[].

Ultima celulă a listei nu va avea un element următor. Avem nevoie de o valoare specială, terminator de listă pe care să o memorăm în vectorul next[] pentru ultima celulă. Aici se practică două variante:

1. Valoarea 0. În acest caz în care nu vom putea folosi celula 0 din perechea de vectori. Vom vedea că nu e chiar o risipă, deoarece de multe ori vom folosi o santinelă pe poziția zero.
2. Valoarea -1. În acest caz putem folosi toate celulele din perechea de vectori.

Operații cu liste

Crearea unei liste cu elemente citite la intrare

Vom folosi -1 ca terminator de listă.

fscanf( fin, "%d", &n );
for ( i = 0; i < n; i++ ) {
  fscanf( fin, "%d", &v[i] );
  next[i] = i + 1;
}
next[n - 1] = -1; // ultimul element din listă

Observăm că fiecare element se leagă de cel de după el, mai puțin ultimul.

Ce complexitate are citirea unei liste?

Desigur O(n), ca și citirea unui vector.

Afișarea unei liste

i = 0;
while ( i != -1 ) { // avem o celulă din listă, nu terminatorul
  fprintf( fout, "%d ", v[i] ); // afișăm elementul listei
  i = next[i]; // trecem la următorul element din listă
}
fprintf( fout, "\n" );

Ce complexitate are scrierea unei liste?

Desigur O(n), ca și scrierea unui vector.

Inserare element în listă după celula i

Să presupunem că la poziția i avem celula cu elementul 45, ca mai jos. Dorim să inserăm o celulă cu elementul 12, aflată la poziția pos imediat după celula i. Iată cum vom proceda:

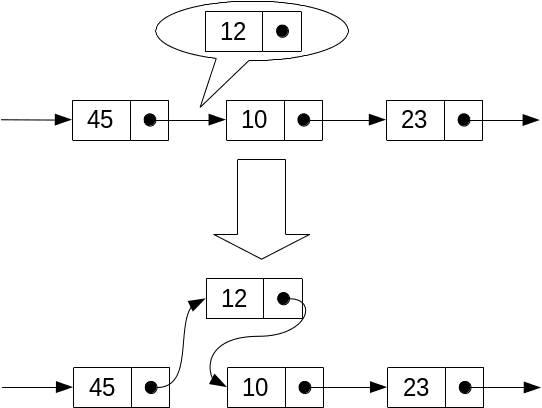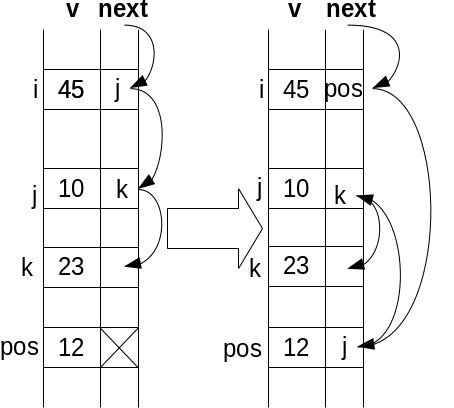Inserare element - concept	Inserare element - implementare // pos conține poziția nodului de inserat next[pos] = next[i]; next[i] = pos;
Inserare element în listă după elementul i

Ce complexitate are inserarea?

Desigur, O(1). Comparați cu un vector, unde inserarea este O(n).

Ștergere din listă a celulei aflate după celula i

Să presupunem că la poziția i avem celula cu elementul 45, ca mai jos. Dorim să eliminăm celula care apare în listă după celula i, cea cu elementul 10, aflat la poziția j. Iată cum vom proceda:

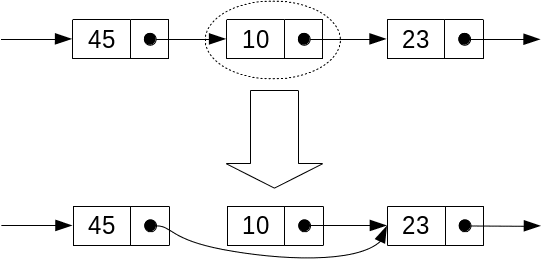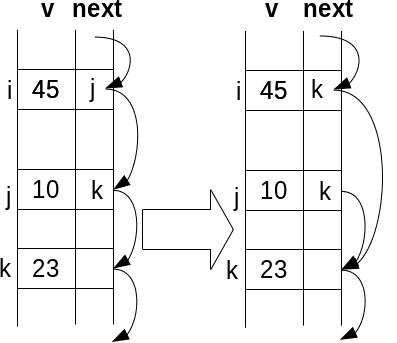Ștergere element - concept	Ștergere element - implementare next[i] = next[next[i]];
Ștergere element din listă după elementul i

Ce complexitate are ștergerea?

Desigur, O(1). Comparați cu un vector, unde ștergerea este O(n).

Valoarea elementului numărul k în listă

Pentru a afla valoarea celui de-al k-lea element în listă va trebui să parcurgem primele k elemente, de la începutul listei. Să presupunem că prima celulă din listă este i. Atunci codul va fi:

  for ( j = 1; j < k; j++ ) // vom avansa de k-1 ori
    i = next[i];            // avansam la urmatoarea celula din lista
  printf( "Elementul numarul %d in lista este %d\n", k, v[i] )

Ce complexitate are aflarea elementului k?

Ea este O(k). Comparați cu un vector, unde este O(1).

Aplicație 1: v-ați ascunselea

n copii numerotați de la 1 la n și așezați în cerc numără la v-ați ascunselea, din k în k, începînd cu copilul 1. Date n și k să se afișeze ordinea în care ies copiii din cerc.

O rezolvare simplă este să memorăm numerele de la 1 la n într-un vector și apoi să avansăm k elemente și să afișăm elementul curent, iar apoi să îl setăm pe zero. Reluăm căutarea de n ori, ignorînd elementele zero:

#include <stdio.h> int v[100]; int main() { int n, k, i, j, pos; scanf( "%d%d", &n, &k ); for ( i = 0; i < n; i++ ) v[i] = i + 1; pos = n - 1; for ( i = 0; i < n; i++ ) { // avanseaza k elemente nenule for ( j = 0; j < k; j++ ) { pos = (pos + 1) % n; while ( v[pos] == 0 ) pos = (pos + 1) % n; } printf( "%d ", v[pos] ); v[pos] = 0; } printf( "\n" ); return 0; }

Numărare în cerc, soluție cu vector

Ce complexitate are acest algoritm? Dacă mai avem i copii în cerc îi vom număra de k/i ori. Restul elementelor fiind zero, vom face k/i parcurgeri ale întregului vector. Dacă considerăm că pornim cu k aproximativ egal cu n, vom face circa n*k/i avansuri. Rezultă numărul de operații total (considerînd k = n ca fiind

Număr operații = n*n/n + n*n/(n-1) + n*n/(n-2) + ... + n*n/2 + n*n/1.

Dăm factor comun n²:

Număr operații = n²(1/n + 1/(n-1) + 1/(n-2) + ... + 1/2 + 1/1).

Suma dintre paranteze va fi studiată în clasa a zecea. Ea este aproximativ log n. Rezultă complexitatea soluției: O(n²log n).

Observăm o anume risipă în această soluție: deși avem poate doar doi copii în listă, noi vom număra pînă la k. Putem optimiza algoritmul numărînd pînă la k % i, unde i este numărul de copii rămași în cerc.

Iată o soluție care folosește această idee:

#include <stdio.h>

int v[100];

int main() {
  int n, k, i, j, pos, a;

  scanf( "%d%d", &n, &k );
  for ( i = 0; i < n; i++ )
    v[i] = i + 1;
  pos = n - 1;
  for ( i = n; i > 0; i-- ) { // numarul de copii scade de la n la 0             
    // numarul de copii ramasi in cerc este i                                    
    // avansam k % i deoarece nu are rost sa numaram dincolo de numarul          
    // de copii din cerc                                                         
    a = k % i == 0 ? i : k % i; // trebuie sa avansam macar un copil             
    for ( j = 0; j < a; j++ ) {
      pos = (pos + 1) % n;      // avansam indicele - numaram copilul            
      while ( v[pos] == 0 )     // gasim urmatorul copil                         
        pos = (pos + 1) % n;
    }
    printf( "%d ", v[pos] );
    v[pos] = 0;
  }
  printf( "\n" );

  return 0;
}

Ce complexitate are această soluție?

La fiecare pas vom trece maxim o dată prin toți copiii rămași în cerc. Vom parcurge, deci, cel mult o dată întregul vector de n elemente. Complexitatea va fi O(n²).

O soluție alternativă propusă de voi este una în care la fiecare pas eliminăm copilul din cerc ștergînd valoarea sa din vector, prin deplasarea elementelor vectorului. Iată acea soluție:

#include <stdio.h>

int v[100];

int main() {
  int n, k, i, j, pos;

  scanf( "%d%d", &n, &k );
  for ( i = 0; i < n; i++ )
    v[i] = i + 1;
  pos = 0;
  for ( i = n; i > 0; i-- ) { // numarul de copii scade de la n la 0             
    pos = (pos + k - 1) % i;  // sarim peste k-1 copii in vector de marime i     
    printf( "%d ", v[pos] );  // afisam copilul                                  
    for ( j = pos + 1; j < i; j++ ) // eliminam copilul din vector               
      v[j - 1] = v[j];
  }
  printf( "\n" );

  return 0;
}

Ce complexitate are această soluție?

De data aceasta avansul la următorul copil este O(1). Dar eliminarea elementului din vector este O(i) pe cazul cel mai rău. Drept care vom avea:

Număr operații = n + (n-1) + (n-2) + ... + 2 + 1

Aceasta fiind suma lui Gauss, rezultă o complexitate O(n²). Ea ne duce însă către o soluție mai bună. Care este pasul scump în această soluție? Eliminarea elementului din vector. Precum am văzut, eliminarea este rapidă într-o listă. Drept care hai să încercăm o soluție cu liste.

Vom așeza numerele de la 1 la n într-o listă. Restul algoritmului este identic cu cel anterior

#include <stdio.h> int v[100], next[100]; int main() { int n, k, i, j, pos; scanf( "%d%d", &n, &k ); // initializam lista for ( i = 0; i < n; i++ ) { v[i] = i + 1; next[i] = (i + 1) % n; } pos = n - 1; // pos e pozitia copilului din-nainte de copilul de eliminat for ( i = 0; i < n; i++ ) { // avanseaza k - 1 elemente deoarece eliminarea conteaza ca un element for ( j = 1; j < k; j++ ) pos = next[pos]; printf( "%d ", v[next[pos]] ); next[pos] = next[next[pos]]; } printf( "\n" ); return 0; }

Numărare în cerc, soluție cu listă

Acum putem elimina copii numărați în mod eficient, dar parcurgerea elementelor nu mai este O(1) ci O(k). Per total complexitatea se reduce la O(n∙k). Pentru k mult mai mic decît n această soluție va fi mult mai bună.

Aplicație 2: bile1

Problema bile1 a fost dată la ONI 2012 clasa a 7^a. Problema poate fi rezolvată folosind o matrice caracteristică a obstacolelor. Dar dacă memoria permisă ar fi fost mai mică nu o puteam rezolva în acest fel. Rezolvarea cu liste necesită doar O(m+n+p) memorie.

Vom memora atîtea liste cîte coloane avem. Fiecare listă va stoca numerele de coloane la care avem obstacole în acea listă. Liniile ce nu au obstacole vor fi reprezentate ca liste vide.

Iată conceptul structurii de date pe care o vom folosi.

Exemplul din problema bile1

Exemplul din desenul problemei - concept structură de date

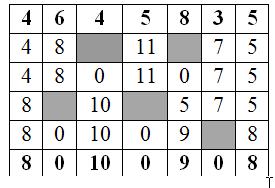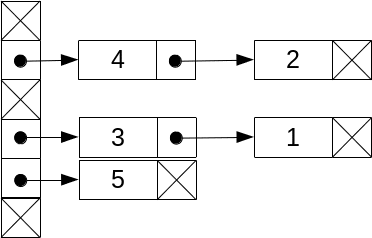Pentru implementare vom folosi ca structuri de date:

• un vector b[n] care memoreaza linia cu bile,n fiind numărul de coloane
• un vector liste[m] care pentru fiercare linie pointează la o listă de coloane pe care se află obstacole, m fiind numărul de linii.
• doi vectori col[p] și next[p] care memorează coloanele obstacolelor și următorul obstacol pe linie, p fiind numărul de obstacole.

Algoritmul folosit este următorul:

1. Citește m, n și p, setează i la zero
2. Citește fiecare obstacol (l, c) si:
  2.1 col[i] = c
  2.2 adaugă coloana c la lista de pe linia l, liste[l]:
    2.2.1 next[i] = liste[l]
    2.2.2 liste[l] = i
  2.3 i = i + 1
3. Citește vectorul de bile
4. Pentru fiecare linie l de la 1 la m
  4.1 parcurge lista de coloane liste[l] si pentru fiecare obstacol col[i] din listă:
    4.1.1 actualizează vectorul de bile la indicele coloanei, col[i]

Cum se compară cu algoritmul inițial care folosește o matrice caracteristică?

Structură de date	Complexitate timp	Complexitate memorie	Explicații
Matrice de frecvență a obstacolelor	$O(m\times n+p)$	$O(m\times n)$	Parcurgerea matricei de frecvență este $O(m\times n)$, iar prelucrarea obstacolelor este $O(p)$
Vector de liste de coloane ale obstacolelor	$O(m+n+p)$	$O(m+n+p)$	Vom parcurge strict obstacolele, de unde rezultă complexitatea $O(p)$. Parcurgem și numerele inițiale, pentru citire, deci $O(n)$. Parcurgem și toate liniile matricei, pentru a verifica dacă avem o listă cu obstacole, deci $O(m)$.

Observăm că atît timpul cît și memoria se îmbunătățesc substanțial. Problema fiind dată la clasa a șasea este puțin probabil că aceasta a fost soluția dorită. Cu toate acestea este un caz de studiu interesant unde o structură simplă de date, pe care olimpici și profesori o ignoră adesea în rezolvarea problemelor de olimpiadă, poate duce la un algoritm simplu și foarte eficient.

Vă rămîne ca temă opțională să implementați această soluție.

Aplicație 3: zigzag

Problema zigzag dată la ONI 2012 clasa a 7^a are o rezolvare foarte ușoară cu liste. Ca și la bile1, vom ține minte pentru fiecare linie a matricei de codificare cîte o listă cu coloanele unde apar litere. Vom genera aceste liste parcurgînd în matrice pozițiile (l, c) unde s-ar afla textul (înainte de a citi acel text!) și adăugînd coloana c la lista liniei l. Apoi vom parcurge aceste liste, în ordine, și vom atașa fiecărei celule, pe lîngă coloană, o literă din text. De fapt vom vedea că nici nu avem nevoie să stocăm coloanele, ci doar literele. În final vom parcurge celulele în ordinea alocării lor, deoarece ea este chiar ordinea textului decodificat.

Iată conceptul structurii de date pe care o vom folosi:

Exemplul din problema zigzag

Exemplul din desenul problemei - concept structură de date

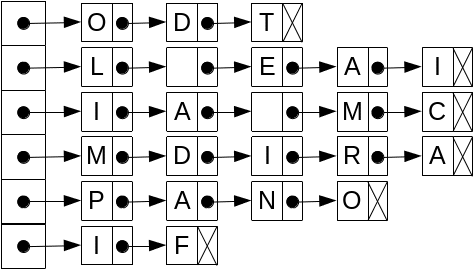O diferență față de bile1 este că va trebui să ținem nu numai vectorul cu începutul listelor ci și un vector cu ultimul element din listă pentru a putea face adăugarea la coadă foarte rapid. O alternativă ar fi să parcurgem pozițiile in ordine inversă (pare mai complicat, însă). Să denumim vectorii prim[] și ultim[].

Iată algoritmul de generare a listelor:

  // pregatim listele cu pozitiile in matricea cheie
  // cheie este cheia, iar n este numărul de caractere al mesajului,
  // c aloca celulele listei si este si coloana in acelasi timp
  l = 0;
  pas = 1; // initial linia creste din unu in unu
  // nu putem avea celule pe indexul 0 deoarece cu zero codificam finalul
  // de lista, deci codificam coloanele incepind cu 1, no biggie
  for ( c = 1; c <= n; c++ ) {
    // pentru fiecare coloana a matricei calculam
    // linia corespunzatoare literei (este una singura!)
    // liniile vor fi de la zero, nici un motiv sa le numerotam de la 1
    // avem perechea (l, c): aseaza c in lista l
    next[c] = 0;          // nu urmeaza nimeni după mine, sint ultima celula
    if ( prim[l] == 0 )   // lista este vida
      prim[l] = ultim[l] = c;
    else                  // avem un ultim element
      ultim[l] = next[ultim[l]] = c;// atasam celula la coada ultimului element

    // avanseaza linia
    l = l + pas;
    if ( l < 0 || l >= cheie ) { // daca am depasit marginea inversam pasul
      pas = -pas;
      l = l + pas + pas; // adunam de doua ori pasul pentru a ne intoarce
    }
  }

Ce complexitate are această soluție?

Este, sper, destul de clar că atît timpul cît și memoria vor fi liniare în numărul de caractere de la intrare. Din nou, folosirea unei liste rezultă într-un algoritm simplu și eficient.

Vă rămîne ca temă să continuați această implementare. Mai aveți de parcurs listele in ordinea naturală și atașat literele din text, iar la final să parcurgeți celulele în ordinea alocării lor (cu indicele c) și să afișați caracterele lor.

Temă

Tema 2 clasa a 7^a

• selecție ca aplicație la algoritmul de selecție (nu trișați, nu aveți voie să apelați funcții de bibliotecă).
• swap dată la ONI 2013 baraj gimnaziu ca aplicație la stive
• bile1 dată la ONI 2012 clasa a 7^a rezolvată cu liste de obstacole.

Tema 2 opțională clasa a 7^a

• zigzag dată la ONI 2012 clasa a 7^a rezolvată cu liste. Vă rog foarte mult să nu luați o rezolvare mai veche și să o trimiteți doar pentru a marca tema ca făcută! Scopul este să exersați listele, nu să luați 100p la problemă!
• la coadă ca aplicație la liste

Rezolvări aici [2]