Clasele 11-12 lecția 11 - 26 nov 2014

Grafuri, partea a doua

În această lecție vom discuta despre diverse tipuri de conexitate în grafuri orientate și neorientate. Determinarea proprietăților de conexitate este o aplicație directă a parcurgerilor (de regulă DFS).

Componente conexe (grafuri neorientate)

Un graf neorientat se numește conex dacă între oricare două noduri există un drum. Componentele conexe ale unui graf sunt subgrafuri conexe maximale (este evident că un nod nu poate aparține mai multor componente conexe). Altfel spus, componentele conexe sunt clase de echivalență ale nodurilor conform relației „este accesibil din” (ce este o relație de echivalență?).

În forma ei cea mai simplă, problema conectivității ne cere să asociem fiecărui nod u o proprietate c[u] astfel încât c[u] = c[v] dacă și numai dacă u și v sunt în aceeași componentă conexă. Putem face aceasta cu o simplă parcurgere DFS:

DFS(nod u, int comp) {
  c[u] = comp;
  foreach (v vecin al lui u) {
    if (c[v] == NIL) {
      DFS(v, comp);
    }
  }
}

DFS-master(graf G) {
  for (u nod în G) {
    c[u] = NIL;
  }
  int comp = 0;
  for (u nod în G) {
    if (c[u] == NIL) {
      DFS(u, comp++);
    }
  }  
}

Rutina DFS-master caută noduri încă neexplorate, care sunt puncte de pornire pentru noi componente conexe. Rutina DFS etichetează recursiv toate nodurile dintr-o componentă.

Conectivitate incrementală (grafuri neorientate)

O problemă des întâlnită este menținerea informațiilor despre conectivitate (în special „sunt u și v în aceeași componentă conexă?”) pe măsură ce în graf sunt adăugate muchii. Această problemă se numește conectivitate incrementală. Aici întâlnim probleme care alternează adăugări de muchii cu întrebări despre accesibilitate (vezi problema Hex).

Vom presupune că ați lucrat deja cu structuri de mulțimi disjuncte (dacă nu, învățați-le curând, căci sunt o unealtă care nu trebuie să vă lipsească din arsenal). Conectivitatea incrementală este o aplicație directă a acestor structuri:

• La adăugarea unei muchii (u, v) în graf, apelăm union(u, v).
• La interogarea dacă u este accesibil din v, comparăm find(u) cu find(v).

Componente tare conexe (grafuri orientate)

Fie un graf G = (V, E). O componentă tare conexă (engl. strongly connected component) este un subgraf maximal al lui G cu proprietatea că între oricare două noduri din subgraf există căi în ambele sensuri.

Ca regulă generală, ce e dificil la această problemă este să evităm să ne „revărsăm” dintr-o componentă într-alta. Cealaltă jumătate a problemei (să vizităm toate nodurile unei componente) este relativ simplă, căci orice parcurgere face asta.

Prezentăm doi algoritmi pentru determinarea componentelor tare conexe.

Algoritmul lui Kosaraju

Graful G cu muchiile de arbore și timpii de finalizare

Graful G^T cu muchiile de arbore și componentele tare conexe

Graful componentelor (dag)

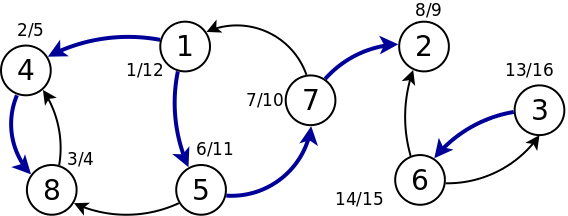
Definim graful transpus G^T = (V, E^T), unde E^T este mulțimea arcelor cu sensul schimbat:

$E^{T}=\{(u,v)|(v,u)\in E\}$

Algoritmul lui Kosaraju face două parcurgeri DFS:

 Componente-tare-conexe(G(V, E)) {
   1. Rulează DFS(G) și reține f[u], timpul de finalizare pentru fiecare nod u.
   2. Calculează graful transpus, DFS(GT).
   3. Rulează DFS(GT), cu precizarea că DFS-master() evaluează nodurile în ordine descrescătoare a lui f.
   4. Fiecare arbore din DFS(GT) este o componentă tare conexă.
 }

Înainte să demonstrăm corectitudinea algoritmului, introducem câteva noțiuni.

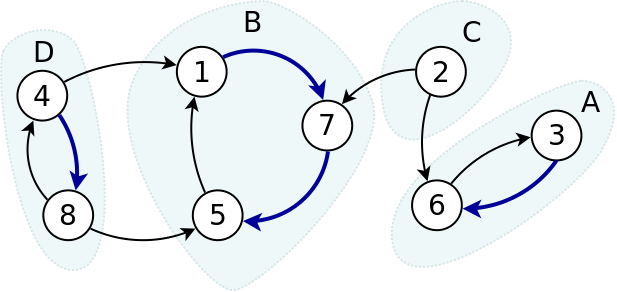
Graful componentelor G^SCC se definește astfel:

• Fiecărei componente conexe C din G îi corespunde un nod C în G^SCC.
• Între două noduri C și C′ din G^SCC există muchie dacă și numai dacă există o muchie (u, v) ∊ E astfel încât u ∊ C și v ∊ C′.

Pentru orice submulțime $C\subseteq V$ definim $d(C)=\min\{d[u]|u\in C\}$ și $f(C)=\max\{f[u]|u\in C\}$. Așadar, $d(C)$ și $f(C)$ sunt primul și ultimul timp când vizităm orice nod din C.

Demonstrația de corectitudine are următorii pași:

Graful componentelor este aciclic.

Demonstrație: dacă graful componentelor ar fi ciclic, atunci fie C și C′ două componente de pe acel ciclu. Toate nodurile din C sunt accesibile din C′ și invers, deci C și C′ ar trebui să fie o singură componentă tare conexă.

Componentele din care ies muchii sunt finalizate mai târziu

Fie două componente C și C′ între care există o muchie, așadar $\exists u\in C$, $\exists v\in C'$ a. î. $(u,v)\in E$. Atunci $f(C)>f(C')$.

Demonstrație: dacă C este descoperită prima (în prima parcurgere DFS), atunci din C ne vom „revărsa” în C′, pe care o vom explora complet înainte de a reveni să finalizăm C. Dacă C′ este descoperită prima, atunci ea va fi finalizată complet înainte de a descoperi componenta C. De ce? Deoarece există o muchie $C,C')$, nu poate exista și o muchie ($C',C)$ prin care să ne „revărsăm” din C′ în C.

Componentele din care ies muchii în G^T sunt finalizate mai devreme

Fie două componente C și C′ între care există o muchie în G^T, așadar $\exists u\in C$, $\exists v\in C'$ a. î. $(u,v)\in E^{T}$. Atunci $f(C)<f(C')$.

Demonstrația decurge în mod banal din propoziția anterioară. Din reciproca acestei implicații decurge o completare interesantă: componenta C pentru care f(C) este maxim nu are muchii care ies din ea (în G^T)!

De aceea, tragem concluzia că, la momentul traversării unei componente conexe C (în G^T), toate componentele în care ea s-ar putea „revărsa” au fost deja traversate și marcate ca vizitate.

Temă de discuție: Cu ce seamănă parcurgerea nodurilor în ordinea descrescătoare a lui f[u]?

Temă de discuție: Cum transpunem graful fără a dubla consumul de memorie? Există o metodă cu O(N) memorie suplimentară (nu cu O(M + N)).

Algoritmul lui Tarjan

Algoritmul lui Tarjan face o singură parcurgere DFS, dar ceva mai complexă. El reține, pentru fiecare nod, adâncimea minimă (distanța minimă față de rădăcina arborelui DFS) până la care poate urca nodul însuși sau unul dintre descendenții lui (ne vom reîntâlni cu acest concept și în secțiunea următoare, despre biconexitate).

Algoritmul folosește o stivă, separată de stiva DFS, pentru a reține nodurile care fac parte din componenta tare conexă curentă. Când un nod nu mai poate urca mai sus decât nivelul propriu, el și toate nodurile care îi urmează în stivă sunt eliminate

// returnează adâncimea minimă la care poate urca u
int DFS(int u, int depth) {
  d[u] = depth;
  stack[ss++] = u;  // Pune nodul pe stivă
  onStack[u] = true;
  
  for (v vecin al lui u) {
    if (d[v] == NIL) {                // Muchie de arbore
      d[u] = MIN(d[u], DFS(v, depth + 1));
    } else if (onStack[v]) {       // Muchie înapoi
      d[u] = MIN(d[u], d[v]);
    } // Altfel este o muchie înainte sau muchie cross către altă componentă conexă
  }

  if (d[u] == depth) {
    // Dacă u nu poate urca mai sus de u, atunci el este rădăcina unei CTC
    // Scoate CTC de pe stivă și o etichetează
    do {
      v = stack[--ss];
      onStack[v] = false;
      scc[v] = numScc;
    } while (v != u);
    numScc++;
  }

  return d[u];
}

Demonstrație de corectitudine. Trebuie să arătăm că u și v vor fi scoase de pe stivă la același moment dacă și numai dacă ele fac parte din aceeași componentă tare conexă.

Componente biconexe, puncte de articulație, punți (grafuri orientate)

Fie G = (V, E) un graf neorientat conex.

G este biconex dacă, după eliminarea oricărui nod și a muchiilor adiacente, el rămâne conex.

O punte este o muchie prin a cărei eliminare G devine neconex. Similar, un punct de articulație este un vârf prin a cărui eliminare G devine neconex.

O componentă biconexă este un set maximal de muchii (și nodurile incidente) astfel încât oricare două muchii sunt pe un ciclu comun. Sinonim, o componentă biconexă este un set maximal de muchii (și nodurile incidente) care să nu conțină punți. De ce sunt cele două definiții echivalente?

Discuție despre găsirea bcc, a punților și a punctelor de articulație cu o parcurgere DFS (Tarjan).

Exerciții

Mici puzzle-uri teoretice. Sunt adevărate următoarele afirmații? Demonstrați că da sau dați un contraexemplu.

• (Cormen 22.3-7) Dacă există o cale de la u la v și d[u] < d[v], atunci v este urmaș al lui u în DFS.
• (Cormen 22.3-8) Dacă există o cale de la ula v atunci d[v] <= f[u].
• (Cormen 22.3-10) Dacă u are muchii care intră și muchii care ies, atunci u nu poate fi singur în arborele lui DFS.
• (Cormen 22.5-3) Putem să simplificăm algoritmul lui Kosaraju astfel: ordonăm nodurile crescător după f[u] și facem a doua parcurgere tot pe G, nu pe G^T. (Indiciu: pentru un nod u ∊ C este posibil ca f[u] să fie mic, însă f(C) să fie foarte mare).
• Nodurile adiacente unei punți sunt puncte de articulație.
• Un punct de articulație are cel puțin o punte adiacentă.

Aplicații și probleme

În limita timpului:

• 2-SAT, reducerea la componente conexe
• Probleme de pe Infoarena / Varena

Temă

• Tema 8 seniori