Clasele 11-12 lecția 24 - 25 mar 2015
În această lecție, vom încerca să găsim o structură arborescentă care să ne ofere toate operațiile comune în timp logaritmic sau mai bun: căutare, inserare, ștergere etc. Avem deja skip lists, dar două structuri sunt mai bune decât una. :-)
Arbori binari aleatori
Pornim de la arborii binari de căutare. Ei sunt ușor de implementat, dar pot degenera dacă cheile sunt inserate în ordine crescătoare / descrescătoare, ducând la timpi de căutare liniari. Dar dacă cheile sunt date într-o ordine aleatoare? Sau, o altă întrebare de ordin practic: dacă ne permitem să citim întâi toate cheile, apoi să le ordonăm aleator și să le inserăm în arbore?
Să considerăm toate permutările mulțimii { 1, 2, ..., n }. Pentru fiecare din ele, construim un arbore binar de căutare inserând cele n numere în ordinea dată de permutare. Observăm că numai două permutări generează arbori complet degenerați (lanțuri): permutările sortate crescător sau descrescător. În schimb, mult mai multe permutări generează arbori perfect echilibrați, de exemplu arbori cu 4 niveluri pentru 15 elemente.
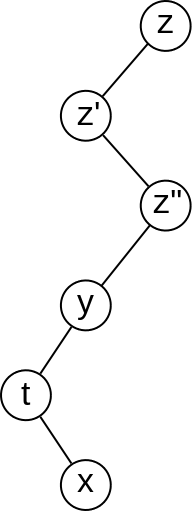
Intuitiv, arborii aleatori vor fi bine echilibrați, dar care este înălțimea medie? Această întrebare este grea, dar putem răspunde la o alta înrudită, mai simplă: dat fiind un nod oarecare x, care este adâncimea lui așteptată?
Să răspundem întâi la întrebarea: care este probabilitatea ca y să fie strămoș al lui x?
Fie z rădăcina arborelui. Așadar, z a fost inserat înainte de y și de x. Pentru ca y să poată fi strămoș al lui x, este important ca x și y să fie (numeric) de aceeași parte a lui z, altfel x și y ar fi în subarbori diferiți. Din același motiv, trebuie ca și nodurile z′, z′′ și orice alte noduri de pe calea dintre z și y să nu se afle (numeric) între x și y. Nodul t și orice alți descendenți ai lui y nu afectează relația între x și y.
Rezultă că x este strămoș al lui y dacă y a fost primul element din intervalul [x, y] care să fie inserat în arbore. Probabilitatea acestui eveniment este
De aici deducem că elementele x - 1 și x + 1 vor fi strămoși ai lui x cu probabilitatea 1/2, x - 2 și x + 2 cu probabilitatea 1/3 etc. Acum, adâncimea așteptată a unui nod nu este altceva decât numărul așteptat de strămoși, adică:
Arbori cartezieni
Un arbore cartezian este un arbore binar asociat unui vector V. Arborele este definit recursiv astfel:
- nodul minim din vector, fie el pe poziția i, este rădăcina arborelui
- nodurile 0 ... i - 1 constituie arborele stâng
- nodurile i + 1 ... n - 1 constituie arborele drept
Dacă valorile din V nu sunt distincte, atunci la un nivel putem alege oricare dintre minime drept rădăcină.
Putem construi V în folosind o stivă ordonată (cum?).
Un al doilea mod de construcție calculează voi vectori ST[i] și DR[i], unde ST[i] este indicele primului element din stânga lui i care are valoare mai mică decât V[i]. DR[i] este definit similar. Acum, părintele lui i este elementul cu valoare maximă dintre ST[i] și DR[i] (de ce?).
Arborele cartezian are două proprietăți interesante:
- proprietatea de heap
- la o parcurgere în inordine obținem arborele original
Aplicație
Folosim arborii cartezieni pentru a reduce problema RMQ la problema LCA. Dându-se un vector pe care dorim să-l preprocesăm pentru RMQ, putem transforma problema într-o problemă de LCA:
- construim arborele cartezian al vectorului
- în acel arbore, minimul dintre pozițiile x și y este elementul de înălțime minimă dintre pozițiile x și y, adică exact LCA(x, y).
Treaps
Arborii binari de căutare sunt ușor de implementat. Ei oferă timp logaritmic, dar numai când cheile sunt distribuite cât mai aleator. Putem să ne folosim de această observație pentru a obține timp logaritmic și când cheile sunt oferite într-o ordine defavorabilă (de exemplu sortată). Vom introduce noi înșine un factor aleator.
Un treap este un arbore binar peste o colecție de perechi (cheie, prioritate) cu proprietățile:
- Dacă îl parcurgem în inordine, cheile sunt sortate crescător.
- Prioritățile respectă condiția de min-heap.
În practică, cheile sunt date la intrare, iar prioritățile sunt generate aleator pentru fiecare nod nou. Acest arbore se numește treap pentru că combină un arbore (tree) cu un heap.
Conceptual, un treap este echivalent cu un arbore binar de căutare în care inserăm cheile într-o ordine aleatoare, dată de priorități. Frumusețea structurii constă în faptul că nu necesită la intrare cheile în această ordine, ci în orice ordine. Un treap poate fi văzut și ca un arbore cartezian al priorităților, construit după ce ordonăm perechile după cheie.
Pentru orice colecție de perechi (cheie, prioritate), treapul asociat există și este unic (de ce?).
Iată o schiță de demonstrație că treapul este echilibrat. Cu probabilitate de 50%, subarborii au maxim 3 n / 4. De ce? Să ne uităm care din cele n noduri ar putea fi ales drept rădăcină. Alegerea se face după un criteriu aleator (prioritatea). De aceea, cu probabilitate de 50%, rădăcina va fi unul din nodurile de la n / 4 la 3 n / 4. Așadar, subarborii scad geometric, iar numărul de niveluri este logaritmic.
Operații
- inserare: Inserăm perechea conform cheii, ca într-un arbore binar. Apoi îi generăm o prioritate aleatoare. Apoi facem rotații cât timp prioritatea nodului este mai mică decât a părintelui său
- căutare: Căutăm ca într-un arbore normal, ignorând prioritățile.
- ștergere: Ștergem nodul și îl înlocuim cu următorul (sau anteriorul) în ordine sortată, pentru a păstra ordonarea cheilor. Apoi facem rotații pentru a respecta condiția de heap.
Treapul ne oferă și operația split, care împarte treapul în două treapuri, cu chei mai mici, respectiv mai mari sau egale cu un x dat. Pentru aceasta, inserăm perechea (x, -1) în treap. Având prioritate minimă, nodul va urca până la rădăcină. Acum fiul stâng și cel drept sunt treapuri care conțin valori mai mici sau egale cu x, respectiv mai mari sau egale cu x. Dacă pot exista chei egale, iau naștere cazuri particulare.