Geometrie computațională (introducere)

Aplicații

Geometria computațională are nenumărate aplicații în informatică:

robotică, roboți autonomi, machine vision
grafică 2D (hărți, GPS, probleme de vizibilitate pe segmente și dreptunghiuri)
grafică 3D (jocuri)
modelarea 3D a moleculelor în căutarea de medicamente

Elemente de geometrie analitică

În geometria computațională ajută să aveți memorie bună ca să rețineți un repertoriu de formule utile.

Ecuația dreptei

Ecuația dreptei poate fi exprimată în multe forme:

${\frac {x-x_{1}}{x_{2}-x_{1}}}={\frac {y-y_{1}}{y_{2}-y_{1}}}$ este dreapta care trece prin punctele $(x_{1},y_{1})$ și $(x_{2},y_{2})$ .
$y-y_{1}=m(x-x_{1})$ este dreapta care trece prin punctul $(x_{1},y_{1})$ și are pantă $m$ . Panta este tangenta unghiului format de dreaptă cu axa Ox.
$y=mx+y_{0}$ (numită în engleză slope + y-intercept) este dreapta care trece prin punctul $(0,y_{0})$ și are pantă $m$ .
$y_{0}x+x_{0}y-x_{0}y_{0}=0$ (numită în engleză x-intercept + y-intercept) este dreapta care taie axele Ox și Oy în punctele $(x_{0},0)$ și $(0,y_{0})$

Aceste formule se demonstrează prin asemănarea triunghiurilor dreptunghice. Toate se pot rescrie în forma generală a ecuației dreptei,

$ax+by+c=0$

De expandat: ecuații parametrice și vectoriale.

Panta unei drepte

Dându-se o dreaptă prin ecuația generală ax + by + c = 0, panta dreptei este $-{\frac {a}{b}}$ . Putem observa aceasta rescriind ecuația ca $y=-{\frac {a}{b}}x-{\frac {c}{b}}$ , care corespunde formei slope + y-intercept.

Intersecția a două drepte

Date fiind două drepte, ax + by + c = 0 și dx + ey + f = 0, punctul lor de intersecție se determină, evident, rezolvând sistemul de ecuații în x și y.

Drepte paralele, perpendiculare

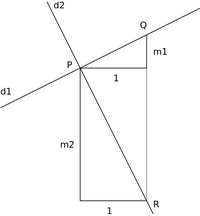
Două drepte sunt paralele când formează unghiuri egale cu orizontala, adică au pante egale: $-{\frac {a}{b}}=-{\frac {d}{e}}$ sau $ae=bd$

Două drepte sunt perpendiculare când produsul pantelor este egal cu -1: $-{\frac {a}{b}}\cdot -{\frac {d}{e}}=-1$ sau $ad+be=0$

Schiță de demonstrație: vezi figura. Fie dreptele $d_{1}$ și $d_{2}$ cu pantele $m_{1}$ și $m_{2}$ . Din punctul de intersecție, P, construim punctele Q și R. Remarcăm că Q și R sunt pe aceeași verticală. Reținem că $m_{2}$ este negativ. Cum triunghiul PQR este dreptunghic, aplicăm teorema lui pitagora:

$PQ^{2}+PR^{2}=QR^{2}$

$1+m_{1}^{2}+1+m_{2}^{2}=(m_{1}-m_{2})^{2}$

$m_{1}m_{2}=-1$

Separarea planului

Evident, expresia ax + by + c va fi zero pentru toate punctele (x, y) de pe dreaptă (în mod tautologic). Ce este interesant este că expresia are valori pozitive pentru toate punctele de o parte a dreptei și valori negative pentru toate punctele de cealaltă parte a dreptei.

De care parte? Nu putem spune exact, căci dreapta ax + by + c este confundată cu dreapta - ax - by - c, care are semnele schimbate. Dar tot ce contează este ca programul vostru să proceseze consecvent toate dreptele.

Test de orientare

O întrebare frecventă este: dându-se trei puncte A, B, și C, sunt ele (a) date în ordine trigonometrică sau (b) date în ordine orară sau (c) coliniare?

Putem reformula întrebarea în două feluri echivalente:

Dându-se A, B și C, segmentul BC cotește, față de segmentul AB, (a) la stânga sau (b) la dreapta sau (c) nu cotește?
Dându-se A, B și C, punctul C este, față de segmentul orientat AB, (a) la stânga sau (b) la dreapta sau (c) pe linie?

Putem răspunde la întrebare muncitorește: calculăm ecuația dreptei AB sub forma ax + by + c = 0 și înlocuim coordonatele punctului C în această ecuație. Mai simplu, Pornim de la ecuația dreptei care trece prin două puncte, trecem totul în partea stângă și înlocuim x și y cu x_C și y_C. Obținem:

$(x_{B}-x_{A})(y_{C}-y_{A})-(x_{C}-x_{A})(y_{B}-y_{A})\gtrless 0$

Putem exprima mai elegant această formulă printr-un determinant:

${\begin{vmatrix}x_{A}&y_{A}&1\\x_{B}&y_{B}&1\\x_{C}&y_{C}&1\end{vmatrix}}\gtrless 0$

Dacă determinantul este pozitiv, punctele sunt date în ordine trigonometrică (traiectoria ABC cotește la stânga).
Dacă determinantul este negativ, punctele sunt date în ordine orară (traiectoria ABC cotește la dreapta).
Dacă determinantul este zero, punctele sunt coliniare.

Observații privind implementarea

Cazuri particulare

O bună parte din arta implementării unui algoritm de geometrie computațională este tratarea cazurilor particulare:

coliniaritate
intersecții exact la un capăt al segmentului
pante infinite (pentru drepte verticale)

Uneori puteți elimina cazurile particulare scriind bine formula. Exemplu: două puncte $P(x_{1},y_{1})$ și $Q(x_{2},y_{2})$ sunt coliniare cu originea dacă ${\frac {y_{1}}{x_{1}}}={\frac {y_{2}}{x_{2}}}$ . Dar această formulă are cazuri particulare: fracțiile sunt nedefinite când $x_{1}$ sau $x_{2}$ sunt 0. Așadar, implementarea de mai jos este greșită.

  if (y1 / x1 == y2 / x2) {
    ...
  }

Putem trata punctele de pe axa Ox printr-un caz particular, sau, mai simplu, putem înlocui formula cu una echivalentă, dar fără împărțiri:

  if (y1 * x2 == y2 * x1) {
    ...
  }

De expandat: Funcții ca atan2(), care gestionează și cazuri particulare.

Erori de calcul

În gcc, tipurile float, double și long double au 4, 8 și respectiv 16 octeți. Țineți minte aceste numere ca să vă puteți face necesarul de memorie.

Indiferent de precizie, în funcție de problemă puteți ajunge la valori ușor diferite pentru formule teoretic egale, în funcție de ordinea operațiilor. De aceea poate fi mai sănătos să nu testați egalitatea cu

  if (x == y) {
    ...
  }

, ci cu

  if (fabs(x - y) < 1e-5) {
    ...
  }

Funcțiile de valoare absolută sunt fabsf() pentru float, fabs() pentru double și fabsl pentru long double. Încă un motiv să lucrați în GNU/Linux, nu în Windows: paginile de manual includ toată documentația pentru GCC.

Operații costisitoare

Țineți minte că adunarea / scăderea, înmulțirea, împărțirea, sqrt, sin / cos, log / exp sunt funcții tot mai costisitoare. Întrebați-vă mereu cum puteți rescrie o formulă pentru a folosi operații cât mai de la începutul listei.

Algoritmul lui Bresenham (pentru segmente)

Pentru a exemplifica observațiile de mai sus, vom discuta algoritmul lui Bresenham. El trasează un segment între doi pixeli (puncte de coordonate întregi) (x₁, y₁) și (x₂, y₂). Se pune, deci, problema enumerării tuturor pixelilor segmentului.

Pentru simplitate, presupunem că segmentul este în primul octant, adică formează un unghi între 0 și 45° cu orizontala. Celelalte 7 cazuri se tratează similar. Ce este special în primul octant? După afișarea punctului (x, y), următorul punct afișat va fi fie (x + 1, y), fie (x + 1, y + 1). Deci algoritmul are de luat o decizie relativ ușoară la fiecare avansare a lui x.

Algoritmul naiv spune: datorită unghiului, toți pixelii au coordonata x diferită. Iterăm deci de la x₁ la x₂ și calculăm coordonata y corectă pe acea coloană. Ea se obține rotunjind coordonata y teoretică la cel mai apropiat întreg.

  for (int x = x1; x <= x2; x++) {
    y = (double)(y2 - y1) / (x2 - x1) * (x - x1) + y1;
    int yint = round(y);
    // afișează pixelul (x, yint)
  }

Acest algoritm face împărțiri pe numere reale, care sunt scumpe.

O variantă mai bună precalculează panta și face împărțiri și înmulțiri înainte de bucla principală, iar în buclă face doar adunări. Ideea este că, de câte ori x crește cu 1, y crește cu valoarea pantei. Apoi y este rotunjit la cel mai apropiat inel.

  double p = (double)(y2 - y1) / (x2 - x1);
  double y = y1;
  for (int x = x1; x <= x2; x++) {
    int yint = round(y);
    // afișează pixelul (x, yint)
    y += panta;
  }

Pentru următoarea variantă, nu mai reținem coordonata reală y, ci coordonata întreagă și abaterea dintre cele două, care va fi mereu cuprinsă între -0.5 și 0.5. Nu obținem nicio îmbunătățire de viteză, dar pregătim terenul pentru ultima variantă, care operează doar pe variabile întregi.

  double p = (double)(y2 - y1) / (x2 - x1);
  double abatere = 0.0;
  int y = y1;
  for (int x = x1; x <= x2; x++) {
    // afișează pixelul (x, y)
    abatere += panta;
    if (abatere > 0.5) {
      y++;
      abatere -= 1;
    }
  }

În sfârșit, dorim să înlocuim variabilele reale p și abatere cu variabile întregi. Pentru acestea, amplificăm toate operațiile pe ele cu x₂ - x₁. Atunci p devine y₂ - y₁. Atenție, și constantele 0.5 și 1 trebuie amplificate! Iar pentru a elimina constanta 0.5, amplificăm testul de inegalitate cu 2.

  int abatere = 0;
  int y = y1;
  for (int x = x1; x <= x2; x++) {
    // afișează pixelul (x, y)
    abatere += y2 - y1;
    if (2 * abatere > x2 - x1) {
      y++;
      abatere -= x2 - x1;
    }
  }

Observăm că acum abaterea va fi mereu cuprinsă între $\pm {\frac {x_{2}-x_{1}}{2}}$ . Pentru maximum de eficiență, înmulțirea cu 2 poate fi exprimată ca shiftare, iar cantitățile x₂ - x₁ și y₂ - y₁ pot fi precalculate în afara buclei.

Probleme

Cele mai apropiate puncte (closest pair)

Enunț: Dându-se n puncte în plan, să se găsească distanța minimă între oricare două dintre ele.

Algoritmul naiv compară toate perechile în $O(n^{2})$ . Vom prezenta un algoritm divide et impera care funcționează în $O(n\log n)$

Să considerăm întâi cazul 1D, când punctele sunt pe axa Ox. Facem abstracție de faptul că putem pur și simplu sorta punctele pentru un algoritm în $O(n\log n)$ . Căutăm un algoritm generalizabil la 2D.

Alegem un punct m, de exemplu calculând media aritmetică a coordonatelor
Împărțim punctele în două submulțimi, S₁ și S₂, în stânga și respectiv în dreapta lui m.
Calculăm recursiv d₁ = min(S₁).
Calculăm recursiv d₂ = min(S₂).
Calculăm d₃ ca distanța dintre punctul de coordonată maximă din S₁ și punctul de coordonată minimă din S₂.
Returnăm min(d₁, d₂, d₃).

Rezultă că $T(n)=2T(n/2)+O(n)$ , adică $T(n)=O(n\log n)$ .

Cum facem trecerea în 2D? Calculul lui d₃ nu mai poate fi făcut în mod naiv. Fie d = min(d₁, d₂). Să considerăm benzile de lățime d la stânga și la dreapta lui m. Este clar că nu are sens să căutăm distanța mimimă între puncte din S₁ și S₂ dincolo de aceste benzi. Dar chiar și așa, o căutare naivă poate dura $O(n^{2}).$

// TODO imagine cu 6 puncte în jurul lui p.

Putem reduce complexitatea calculului lui d₃ la $O(n\log n)$ observând că, în interiorul acestor benzi, punctele se află la distanță cel puțin d unul de altul; altfel ar fi fost alese ca soluție la subproblema stângă sau dreaptă. De aceea, poate fi necesar să evaluăm cel mult 6 puncte pentru fiecare punct din interiorul benzilor. Putem face aceasta în $O(n\log n)$ sortând după y punctele din fiecare bandă.

Complexitatea algoritmului este acum $T(n)=2T(n/2)+O(n\log n)$ , adică $T(n)=O(n\log ^{2}n)$ .

Pentru a reduce complexitatea la $O(n\log n)$ , trebuie să facem calculul lui d₃ în $O(n)$ . Putem face aceasta dacă cerem ca fiecare subproblemă să returneze lista punctelor sale sortată după y. Atunci calculul lui d₃ se face printr-o interclasare foarte similară cu algoritmul mergesort.

Ca fapt divers, putem demonstra că $O(n\log n)$ este optim, adică nu există algoritmi asimptotic mai buni. Discuție despre reducerea la problema elementelor distincte.

Diametrul unui poligon convex

Enunț: dându-se un poligon convex cu n vârfuri, să se determine diametrul poligonului, adică distanța maximă între două puncte ale sale.

Există un algoritm în O(n), descoperit de Shamos în 1978. El are la bază un principiu mult mai general, șublerul rotitor (rotating calipers). Să ne imaginăm că rotim un șubler de jur împrejurul poligonului, reglându-l la fiecare moment pentru a măsura exact poligonul. Deschiderea maximă a șublerului la orice moment ne dă diametrul poligonului.

// TODO imagine

Alternativ, ne putem imagina că rostogolim poligonul pe podea și, la fiecare moment, măsurăm înălțimea la care ajunge. Înălțimea maximă este diametrul.

Terminologie:

O dreaptă suport este o dreaptă care trece printr-un vârf al poligonului astfel încât tot interiorul poligonului să se afle de aceeași parte a dreptei.
- O dreaptă suport poate conține în întregime o latură a poligonului.
- Dreapta suport nu este unică pentru un vârf. Printr-un vârf pot trece un fascicul de drepte suport.
O pereche de vârfuri antipodale este o pereche de vârfuri care admit drepte suport paralele.
Diametrul este distanța maximă între drepte suport paralele.

Un algoritm naiv ar putea porni cu drepte suport orizontale care trec prin punctele de y minim și maxim. Apoi ar roti aceste drepte puțin câte puțin, până la următorul eveniment „interesant”.

Discuție despre câte evenimente „interesante” există și despre ineficiența operațiilor de calculare a unghiurilor.

Algoritmul eficient enumeră toate perechile de puncte antipodale și o alege pe cea cu distanța maximă. Funcția next() returnează următorul punct în mod circular.

  ALGORITM: Puncte antipodale
  // Pornim cu p = p[n] și q = punctul cel mai depărtat de dreapta p[n]p[1]
  p = p[n];
  q = p[1];
  while (area(p, next(p), next(q)) > area (p, next(p), q)) {
    q = next(q);
  }

  // Rotim șublerul până am schimbat p și q între ele
  q0 = q;
  while (q != p[n]) {
    p = next(p);
    print(p, q);
    while (area(p, next(p), next(q)) > area (p, next(p), q)) {
      q = next(q);
      print(p, q);
    }
    if (area(p, next(p), next(q)) == area (p, next(p), q)) {
      print(next(p), q);
    }
  }

Algoritmul original este puțin mai complex, deoarece evită să tipărească aceeași pereche de mai multe ori. Algoritmul prezentat mai sus nu face acest efort.

Alte probleme similare:

Să se afle lățimea unui poligon convex, adică distanța minimă între două drepte suport.
Să se afle distanța maximă (sau minimă) între două poligoane convexe.
Să se afle dreptunghiul minim (ca arie sau ca perimetru) în care poate fi încadrat un poligon convex.

Temă

Tema 1 seniori

Clasele 11-12 lecția 2 - 24 sep 2014

Contents