Clasele 11-12 lecția 4 - 8 oct 2014
Discuție despre facultăți
Numai în măsura în care voi aveți întrebări. Cristi și eu vă putem da câteva sfaturi generale despre:
Facultăți în România și în afara României. Nu merită să plecați oriunde!
Studii de licență (undergrad) și studii doctorale (grad school). Comparația cu România diferă mult la cele două capitole.
Mediul academic și mediul industrial. Vreți să fiți ingineri sau profesori? Nu este nevoie să vă hotărâți de acum, :-) dar există asemănări și deosebiri.
Procesul de pregătire. Durează un an și unele etape depind de oameni leneși / ocupați (foaia matricolă tradusă, scrisorile de recomandare)
Merită să furnizați date pe care universitățile nu le cer? Clar da. Dați niște SAT-uri, chiar și pentru Europa. Faceți rost de (sau creați voi) un rezumat al programei, cel puțin pentru info / mate / fizică. Voi trăiți într-o țară unde toți elevii fac integrale și teoria relativității în liceu. Nici nu știți cât de mult cântărește asta în favoarea voastră.
Probleme de la OJI din anii trecuți
Iată și o arhivă cu enunțurile și soluțiile comisiei.
OJI 2014: Fracții 2
Infoarena: 2014 Fracții2
Cuvinte-cheie: programare dinamică, recurență
Primul punct este simplu. Putem scrie în fișierul de ieșire
1 2 3 ... n-2 n-1 n-1
deoarece
Partea dificilă este punctul 2. Fie n = 4. Vrem să scriem numărul 2/2 ca sumă de 4 fracții cel mult egale cu 1/2. Atunci:
- putem să nu folosim fracții 1/2 și rămânem cu 2/2 (adică 4/4) care trebuie exprimat ca sumă de 4 fracții cel mult egale cu 1/4, sau
- putem să folosim o fracție de 1/2, caz în care rămânem cu 1/2 (adică 2/4) care trebuie exprimat ca sumă de 3 fracții cel mult egale cu 1/4, sau
- putem să folosim două fracții de 1/2, caz în care rămânem cu 0, care trebuie exprimat ca sumă de 2 fracții (acest caz este evident imposibil).
Să luăm un caz dintr-un arbore mai adânc. Să spunem că vrem să scriem numărul 6/8 ca sumă de 10 fracții cel mult egale cu 1/8. Atunci:
- putem să nu folosim fracții 1/8; rămânem cu 6/8, adică 12/16, care trebuie scris ca sumă de 10 fracții cel mult egale cu 1/16. (Aceasta este imposibil)
- putem să folosim o fracție 1/8; rămânem cu 5/8, adică 10/16, care trebuie scris ca sumă de 9 fracții cel mult egale cu 1/16. (Și aceasta este imposibil)
- putem să folosim două fracții 1/8; rămânem cu 4/8, adică 8/16, care trebuie scris ca sumă de 8 fracții cel mult egale cu 1/16. (Există o singură soluție: 1/16 + ... + 1/16)
- putem să folosim trei fracții 1/8; rămânem cu 3/8, adică 6/16, care trebuie scris ca sumă de 7 fracții cel mult egale cu 1/16. (Există o singură soluție; o vedeți?)
- putem să folosim patru fracții 1/8; rămânem cu 2/8, adică 4/16, care trebuie scris ca sumă de 6 fracții cel mult egale cu 1/16. (Există soluții multiple)
- putem să folosim cinci fracții 1/8; rămânem cu 1/8, adică 2/16, care trebuie scris ca sumă de 5 fracții cel mult egale cu 1/16. (Există soluții multiple)
- putem să folosim șase fracții 1/8; rămânem cu 0/8, adică 0/16, care trebuie scris ca sumă de 4 fracții cel mult egale cu 1/16. (Aceasta este imposibil)
Observația-cheie este că numitorii 8 și 16 sunt irelevanți. Am avea exact același arbore de decizie pentru 6/128, adică 12/256. Important este că numărătorul se înmulțește cu 2 când trecem la fracții de două ori mai mici.
Așadar, fie numărul de descompuneri în fracții a lui , pentru un p oarecare, folosind fracții cel mult egale cu . Atunci putem alege să folosim k fracții de , iar pe restul de j - k să le transformăm în 2(j - k) fracții de
Condițiile sunt k < i și k < j, în mod evident din partea dreaptă, dar și j ≤ i pentru ca să aibă sens. Rezultă că și în dreapta trebuie să avem
Obținem o primă iterație a codului:
for (int i = 1; i <= n; i++) {
d[i][i] = 1;
}
for (int i = 2; i <= n; i++) {
for (int j = i; j >= 1; j--) {
int start = MAX(2 * j - i, 0);
for (int k = start; k < j; k++) {
d[i][j] += d[i - k][2 * (j - k)];
}
d[i][j] %= MODULO;
}
}
fprintf(f, "%d\n", d[n][2]);
Observații:
- Codul este O(n3).
- Parcurgerea liniilor se face în ordine descrescătoare a lui j, deoarece d(i, j) se referă la d(i, 2j).
- Operația de modulo se face o singură dată, în afara buclei după k. Întrucât modulul este circa 105, iar k iterează de cel mult 2.000 de ori, putem face aceasta. Această optimizare înjumătățește timpul de rulare.
- Calculăm toată matricea d, dar accesăm doar elementele de pe coloane pare.
Ultima optimizare este să calculăm doar coloanele pare din matrice, reducând la jumătate necesarul de memorie. Cu aceste optimizări, estimez că sursa ia 84 de puncte.
Din păcate, și soluția propusă de comisie se oprește la O(n3) (iat-o). Ea nu menționează ultimul pas necesar pentru reducerea la O(n2). Să examinăm d(10, 6) (ignorați faptul că unii termeni din sumă sunt nuli):
În același timp,
așadar
și for-ul după k este înlocuit printr-o singură adunare.
Șmen urât: precalcularea soluției
Observăm că această problemă are doar 2.000 de teste posibile (la punctul 2). În plus, matricea calculată pentru n = 2.000 conține toate celelalte răspunsuri. Dacă nu vă vine ideea de reducere de la O(n3) la O(n2), puteți să rulați în timpul concursului versiunea lentă și să includeți rezultatele într-un vector în program. Nu trebuie incluse toate, ci doar cele de la circa 1.500 la 2.000, pentru care algoritmul lent nu se încadrează în timp. Aveți nevoie de circa 3 KB de cod-sursă pentru aceste numere.
Repet: acest șmen este urât, merge doar pentru anumite probleme și aveți voie să-l folosiți numai la olimpiadă, niciodată la teme.
OJI 2014: Cârtițe
Infoarena: 2014 Cârtițe (atenție, la primul exemplu răspunsul este 4 2 3, nu 4 3 2).
Cuvinte-cheie: algoritmul lui Lee, ciclu eulerian
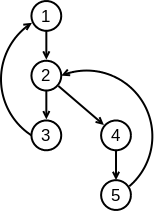
Pentru punctul (a), puteți marca efectiv în matrice:
- pătratele atacate de vulpi ca obstacole
- punctul de plecare al cârtiței ca sursă
- capetele de galerii ca destinații
Apoi, rulați algoritmul lui Lee de la sursă la prima destinație întâlnită.
Pentru punctul (b), aveți nevoie să implementați găsirea unui ciclu Eulerian. Atenție la câteva detalii:
- Nu creați un graf de M*N noduri, căci există cel mult K = 50 galerii. Cum graful este Eulerian, el poate avea cel mult 50 de noduri.
- Mai bine rețineți un vector cu coordonatele fiecărui nod (ca să le puteți tipări).
- Nu uitați că algoritmul naiv pleacă dintr-un nod și traversează muchii la întâmplare. El nu se poate bloca (datorită parității gradelor) și va reveni în același nod, dar poate omite cicluri.
Infoarena are o discuție amplă despre găsirea ciclurilor euleriene. Site-ul face însă o greșeală când pomenește despre algoritmul lui Fleury. Este adevărat că acest algoritm garantează găsirea unui ciclu din prima (nu ratează ramificații), dar principiul lui este:
- Definește graful redus ca fiind graful muchiilor netraversate încă;
- Evită să traverseze punți (muchii critice) în graful redus.
Algoritmul lui Fleury este lent, căci necesită întreținerea dinamică a punților pe măsură ce reducem graful. Soluția propusă de Infoarena este să facem o parcurgere din nodul de start și să etichetăm muchiile ca muchii de arbore (în jos) și muchii de întoarcere (în sus). La plecarea dintr-un nod vom prefera muchii de întoarcere, dacă există. Aș fi curios să văd o demonstrație că această metodă găsește un ciclu din prima. Pe exemplul alăturat, ea merge corect, găsind ciclul 1 - 3 - 2 - 5 - 4 - 2 - 1.
Algoritmul simplu oferă același timp O(|E|) și este mai puțin interpretabil.
- pornim din nodul 1 și traversăm muchii până revenim în nodul 1 și epuizăm toate muchiile acestuia;
- colectăm nodurile vizitate într-o listă circulară dublu înlănțuită;
- iterăm prin această listă;
- dacă, ajungând la nodul u, observăm că el mai are muchii nevizitate, îl traversăm și pe el și inserăm lista de noduri la poziția curentă în listă;
- când ajungem la sfârșitul listei, am obținut un ciclu Eulerian.
OJI 2013: Biperm
Varena: 2013 Biperm
Cuvinte-cheie: grafuri, permutări, descompunerea unei permutări în cicluri, indexare
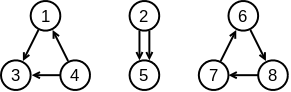
Să considerăm următoarea bipermutare:
| 1 | 7 | 2 | 4 | 2 | 8 | 4 | 6 |
| 3 | 6 | 5 | 1 | 5 | 7 | 3 | 8 |
Acestei permutări îi asociem (fictiv) un graf orientat cu n noduri și n muchii. Dacă în bipermutare i apare deasupra lui j, în graf trasăm muchia (i, j). Vezi figura alăturată. O mutare schimbă sensul unei muchii.
Întrucât matricea este bipermutare, rezultă că fiecare nod are fix două muchii adiacente. De aceea, graful este o colecție de cicluri, dacă ignorăm sensul muchiilor. Alegem un sens de referință și numim muchiile în sens invers „conflicte”. Dacă niciun ciclu nu are conflicte, atunci bipermutarea asociată este perfectă.
Cerințele problemei devin:
- În câte moduri putem întoarce muchii pentru a elimina conflictele?
- Câte muchii trebuie să întoarcem minim pentru a elimina conflictele?
- Eliminați conflictele într-un mod oarecare și tipăriți bipermutarea perfectă asociată.
Răspunsurile sunt:
- 2numărul de cicluri. Ciclurile pot fi rezolvate independent. Dintr-un ciclu cu conflicte putem obține unul fără conflicte în două moduri (inversăm toate muchile care merg în sens orar sau pe toate cele care merg în sens trigonometric). Pentru un ciclu care nu are conflicte, avem opțiunea de a inversa toate muchiile fără a crea conflicte.
- Însumăm, pentru fiecare ciclu, muchiile în fiecare sens și luăm valoarea mai mică. Pentru un ciclu care deja nu are conflicte, această valoare este 0.
- Decurge în mod banal din (1) sau din (2).
Punctul (1) se rezolvă ușor dacă indexăm vectorul. Pentru fiecare valoare între 1 și n, stocăm coloanele cele două apariții.
int b[MAX_N][2]; // vectorul dat la intrare
int ap[MAX_N][2]; // vectorul de apariții
for (i = 0; i < n; i++) {
ap[i][0] = ap[i][1] = -1;
}
for (i = 0; i < n; i++) {
for (j = 0; j < 2; j++) {
if (ap[v[i][j]][0] == -1) {
ap[v[i][j]][0] = i;
} else {
ap[v[i][j]][1] = i;
}
}
}
Apoi, parcurgem vectorul și numărăm ciclurile în O(n) (cum?).
Pentru punctul (2), pe măsură ce numărăm ciclurile, contabilizăm și numărul de muchii în fiecare direcție. De exemplu:
- pe prima coloană avem (1,3). Contorizăm, prin convenție, o muchie în sensul „A”.
- cealaltă apariție a lui 1 este în perechea (4,1). Deoarece 1 apare pe linia de jos, avem tot o muchie în sensul „A”.
- cealaltă apariție a lui 4 este în perechea (4,3). Deoarece 4 apare pe linia de sus, avem o muchie în senul „B”.
- distribuția pe acest ciclu este 2-1, valoarea minimă fiind așadar 1.
Atenție la cazul ciclurilor de lungime 1 (anticipez că nu este nevoie să-l tratăm special, dar trebuie testat).
OJI 2013: Subsecvențe
Varena: 2013 Subsecvențe
Cuvinte-cheie: hash table sau sortare, sau trie, KMP, Rabin-Karp etc. pentru punctaj parțial
Problema are multe variante de rezolvare și multe obțin punctaj parțial (vezi soluția comisiei). Iată alte două soluții mult mai simple, ambele de 100p.
Pentru ambele soluții, ne folosim de faptul că șirurile sunt binare, iar L ≤ 60, deci putem codifica subsecvențele prin numere pe 64 de biți. Mai mult, dacă deplasăm o fereastră de lungime L printr-un șir, putem recalcula codul incremental, în O(1) (cum?).
Vectori + sortare
- Presupunem că lungimea șirului comun este L.
- Iterăm prin toate subsecvențele de lungime L ale tuturor șirurilor.
- Pentru o subsecvență cu codul C din șirul Sk, inserăm într-un vector perechea (C, k).
- Ordonăm vectorul de perechi după coduri.
- Iterăm prin vector și vedem dacă există vreun cod prezent în toate șirurile.
- Deoarece nu știm care este valoarea lui L, o căutăm binar (căutăm cea mai mare valoare pentru care există o subsecvență comună).
Complexitate: O(log L * |S| * log |S|), datorită necesității de a sorta un vector de circa |S| elemente.
Tabelă hash
Folosim o tabelă hash.
- Presupunem că lungimea șirului comun este L.
- Inserăm într-o tabelă hash codul fiecărei subsecvențe de lungime L a fiecărui șir.
- Valoarea asociată unui cod este un număr pe 4 biți, bitul al k-lea indicând că subsecvența apare în Sk.
- Prima oară când întâlnim un cod, îi asociem valoarea 2k (un singur bit setat).
- La apariții ulterioare, îi setăm, în plus, bitul potrivit.
- La final, vedem dacă există vreo cheie în tabelă cu valoarea 111...111.
- Deoarece nu știm care este valoarea lui L, o căutăm binar (căutăm cea mai mare valoare pentru care există o subsecvență comună).
Complexitate: O(log L * |S|), cu constantă mărișoară datorită tabelei hash.