Clasele 11-12 lecția 5 - 15 oct 2014

Iată și o arhivă cu enunțurile și soluțiile comisiei.

OJI 2012: Blis

Infoarena: 2012 Blis

Cuvinte-cheie: subșir crescător în O(n log n), programare dinamică

Găsirea celui mai lung subșir în O(n log n)

Problema Blis devine mult mai ușoară dacă știți deja algoritmul de aflare a celui mai lung subșir crescător în $O(n\log n)$. Îl reluăm sumar.

Cheia algoritmului este un vector min unde min[i] este valoarea minimă în care se poate termina un șir crescător de lungime i. De exemplu, pentru vectorul

 v = ( 1, 4, 3, 5, 6 )
 min = ( ??, 1, 3, 5, 6 )

cu semnificația că cel mai scurt subșir crescător de lungime 2 se termină în 3. Există și alte subșiruri crescătoare de lungime 2, cum ar fi (1, 4), (5, 6) etc., dar cea mai mică valoare finală este 3.

Dacă următorul element din v este 2,

 v = ( 1, 4, 3, 5, 6, 2 )
 min = ( ??, 1, 2, 5, 6 )

cu semnificația că acum a apărut un nou subșir crescător de lungime 2, (1, 2), care se termină în 2. Acesta îi este de preferat lui (1, 3), deoarece avem mai multe șanse să-l extindem cu elemente viitoare.

Schița algoritmului este:

 min[1] = ∞ pentru i = 1, n
 pentru i de la 0 la n - 1
   caută binar cea mai mare poziție j pentru care min[j] < v[i]
   dacă v[i] < min[j + 1]
     min[j + 1] = v[i]

Aplicarea la problema Blis

Ce este nou la această problemă este că vectorul nu este unic determinat. Dar putem aplica același algoritm.

Să presupunem că am calculat vectorul min până la poziția p - 1 inclusiv și acum examinăm bitul de pe poziția p, unde începe un număr nou. Acest număr se va termina la una din pozițiile p, p + 1, ..., p + k - 1. Oricare din cele k numere poate îmbunătăți vectorul min. Totuși, nu le putem procesa pe toate în acest moment. În particular, este greșit să modificăm vectorul în două locuri la evaluarea poziției p, chiar dacă două din cele k numere aduc îmbunătățiri.

Corect este să notăm aceste îmbunătățiri în dreptul pozițiilor p + 1, ..., p + k - 1, apoi să marcăm poziția p ca procesată și să trecem la p + 1. Așadar, orice poziție q va putea primi îmbunătățiri de la q - 1, q - 2, ..., q - k. Procesarea unei poziții p constă din:

• aplicarea tuturor îmbunătățirilor în vectorul min care se mai aplică;
• generarea îmbunătățirilor pentru pozițiile p + 1, ..., p + k, dacă există.

Complexitate: $O(nk\log n)$. Pentru fiecare poziție, trebuie generate cele k n numere începând cu bitul respectiv și fiecare dintre ele trebuie căutat binar în vectorul min.

OJI 2012: Parc

Infoarena: 2012 Parc

Cuvinte-cheie: teorema lui Pitagora, puteri ale lui 2

Aceasta este o problemă de geometrie, ușurată mult de limitele mici. Dacă nu există benzi de bicicletă, Gigel se poate deplasa în linie dreaptă. Benzile de bicicletă îi deformează drumul cu segmente orizontale sau verticale. În exemplul din enunț, Gigel trebuie să se deplaseze pe o diagonală care merge 2 pătrate la dreapta și 4 în sus, deformată cu 5 pași orizontali și 2 verticali. Astfel obținem răspunsul la punctul (1):

$d={\sqrt {2^{2}+4^{2}}}+5+2=11.47213595\ldots$

Putem da acest răspuns în $O(m+n)$. Fie $s_{x}$ suma lățimilor benzilor verticale cuprinse între $x_{G}$ și $x_{pr}$. Fie $d_{x}=|x_{G}-x_{pr}|-s_{x}$. Similar definim $s_{y}$ și $d_{y}$. Atunci Gigel se va deplasa $s_{x}$ pe orizontală, $s_{y}$ pe verticală și restul pe diagonală, deci

$total=s_{x}+s_{y}+{\sqrt {d_{x}^{2}+d_{y}^{2}}}$

Pentru punctul (2), putem sorta vectorii benzilor pe x și pe y, după care îi interclasăm. În exemplul din enunț,

• Știm că Gigel se deplasează cu o tangentă de 1 la 2 (o unitate pe x pentru fiecare două unități pe y)
• Pornind de la (1, 1), următoarele benzi sunt la coordonata 2, atât pe y cât și pe x. Deoarece (2 - 1) / 1 > (2 - 1) / 2, rezultă că Gigel va atinge coordonata y = 2 prima dată, la coordonatele (1,5, 2).
• Apoi Gigel traversează banda, deci îl mutăm la (1,5, 4).
• De aici Gigel va intersecta banda verticală la coordonatele (2,5) etc.
• Dacă în timpul interclasării Gigel atinge simultan o bandă verticală și una orizontală, el le poate traversa în orice ordine, iar numărul de soluții se dublează.
• Ca la orice interclasare, merită să punem santinele (două benzi de lățime 1 la limita parcului).

Direcții de explorat:

• Puteți implementa algoritmul fără a face împărțiri?
• (problemă deschisă) Dacă toate datele de intrare sunt întregi, putem implementa algoritmul doar cu adunări? Eu nu reușesc. Ar trebui să arate ca un Bresenham modificat.

OJI 2011: Suma

Infoarena: 2011 Suma

Cuvinte-cheie: programare dinamică

Aceasta este o problemă de programare dinamică relativ simplă, dar care ne învață niște mecanisme utile de precalculare.

Pentru punctul (1), știm că n este o sumă de pătrate de la 1 la m, deci

$n={\frac {m(m+1)(2m+1)}{6}}$

Cum m este cel mult 57, puteți să-l căutați liniar.

Pentru punctele (2) și (3), ideea programării dinamice este să calculăm costul minim cu care putem ajunge în fiecare cameră de pe nivelul 1, 2, ... m. Presupunând că putem ajunge în camera k dintr-una din camerele x, y, z sau t (pot fi și mai puține când k este pe margine sau în colț), avem recurența

$S(k)=C(k)+min(S(x),S(y),S(z),S(t))$

Întrebarea este: cum stocăm piramida? Ca să nu ne complicăm, putem să creăm o matrice cubică de m³ celule. Pentru m = 57, aceasta înseamnă cam 185.000 de celule, aproximativ triplu față de necesar. În ziua concursului clar așa am proceda, dar putem mai bine de atât?

Conversia între număr și coordonate

Aceasta este o problemă des întâlnită: dându-se un set de obiecte, să se găsească un algoritm de codificare / decodificare astfel încât codurile să fie unice și continue. Exemple:

• permutările (să se codifice o permutare de n elemente cu un număr între 0 și $n!-1$)
• combinările (să se codifice o combinare de n luate câte k cu un număr între 0 și $C_{n}^{k}-1$)
• codul Gray (să se găsească al n-lea număr al lui Gray / poziția în listă a unui număr Gray)

Iată un algoritm simplu pentru a găsi camera de la coordonatele (e, l, c) (etaj, linie, coloană, toate indexate de la 1):

$index={\frac {(e-1)\cdot e\cdot (2e-1)}{6}}+(l-1)\cdot e+c$

Primul termen însumează pătratele numerelor mai mici decât e, al doilea însumează liniile anterioare lui l, iar al treilea coloanele până la c inclusiv.

Iată un algoritm simplu, dar lent, pentru transformarea inversă, din index în coordonate:

• Precalculăm t[e] = numărul ultimei camere de pe etajul e (tot ca sumă de pătrate).
• Pentru un index i, găsim cel mai mic etaj e pentru care i > t[e].
• Scădem t[e] din i.
• Problema găsirii liniei și coloanei lui i într-o matrice de e x e este banală.

Decodificarea durează acum $O(\log m)$, căci vectorul t este ordonat. Pentru a reduce complexitatea la O(1), trebuie să rezolvăm o ecuație de gradul 3 ca să aflăm etajul camerei. Aceasta depășește scopul lecției, dar este de reținut.

Înarmați cu această codificare, putem scrie algoritmul:

  int eu = 0; // indicele camerei curente
  for (int e = 1; e <= m; e++) {
    for (int i = 1; i <= e; i++) {
      for (int j = 1; j <= e; j++) {
        // Nu tratăm aici cazurile speciale, dar ele trebuie tratate
        eu++;
        int sus = codifica(e - 1, i, j); // indicele camerei de deasupra
        d[eu] = c[eu] + min(d[sus], d[sus - 1], d[sus - e + 1], d[sus - e])
      }
    }
  }

Acest cod folosește strict memoria necesară.

OJI 2011: Ubuntzei

Problema Ubuntzei: structura drumului optim

Infoarena: 2011 Ubuntzei

Cuvinte-cheie: Programare dinamică, mulțimea submulțimilor, manipulare de biți, Dijkstra; alți algoritmi de drumuri pentru punctaje parțiale

Putem să ne imaginăm un graf extins cu $n\cdot 2^{k}$ noduri. Un nod (u, S) arată că suntem în nodul u și am vizitat nodurile din mulțimea S. Totuși această abordare este riscantă întrucât $n\cdot 2^{k}=64.000.000$ pentru limitele din problemă.

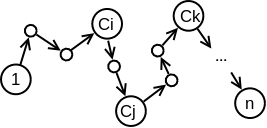
Pentru o abordare mai eficientă, să considerăm structura drumului optim (vezi figura). Drumul pornește din nodul 1 și trece prin nodurile C₁, C₂, ..., C_k într-o ordine anume, apoi se termină în nodul n. Între oricare dintre aceste orașe drumul optim poate folosi orașe intermediare, dar va merge pe traseul minim.

De aceea, vom începe prin a precalcula distanțele minime în graful original. Fie $d$ matricea acestor distanțe. Fie $C=\{C_{1},C_{2},...,C_{k}\}$. De acum înainte, ne vor interesa doar distanțele între noduri din mulțimea $\{1,n\}\cup C$.

Definim $e(u,S)$ = costul minim cu care putem vizita submulțimea $S$ astfel încât să rămânem în nodul $u$ (unde $u\in S$ și $S\subseteq C$. Condițiile inițiale sunt:

$e(u,\{u\})=d(1,u)\ {\mbox{pentru}}\ u\in C$

iar recurența este

$e(u,S)=\min _{v\in S\setminus \{u\}}{\Big \{}e(v,S\setminus \{u\})+d(v,u){\Big \}}$

În final,

$raspuns=\min _{u\in C}{\Big \{}e(u,C)+d(u,n){\Big \}}$

Complexitate

În primul rând, matricea distanțelor trebuie calculată rulând algoritmul lui Dijkstra de k + 2 ori, nu Floyd-Warshall, deoarece ne interesează doar distanțele din $\{1,n\}\cup C$. Pentru limitele problemei, $O(km\log n)$ este incomparabil mai bine decât $O(n^{3})$.

Care este complexitatea calculului matricei $e$? Pentru o submulțime oarecare $S$, sunt definite doar acele valori $e(u,S)$ pentru $u\in S$. De asemenea, o valoare $e(u,S)$ se calculează ca un minim dintre $|S|-1$ valori. Așadar,

$T(n)=\sum _{S\in {\mathcal {P}}(C)}|S|(|S|-1)=\sum _{k=0}^{n}C_{n}^{k}\cdot k(k-1)<\sum _{k=0}^{n}C_{n}^{k}\cdot k^{2}$

Această sumă poate fi calculată cu un program pentru a observa că $T(15)<2.000.000$. Sau, empiric, putem calcula T(2), T(3), T(4), T(5) și observa că

$T(k)=k(k+1)\cdot 2^{k-2}$

Pentru stocarea valorilor, putem folosi o matrice completă de dimensiuni k x 2^k. Unele zone din această matrice nu vor fi folosite, căci $e(u,S)$ este nedefinită când $u\notin S$. Matricea risipește exact 50% din spațiu. Puteți demonstra de ce?

Temă

• Tema 4 seniori