Clasele 11-12 lecția 6 - 22 oct 2014
Din ultimele două lecții au rezultat două subcapitole care merită o lecție împreună.
Operații pe biți
Aplicația directă a operațiilor pe biți este posibilitatea de a stoca variabile pe mai puțin de un octet, ceea ce poate duce la economie uriașă de memorie. Uneori putem câștiga și timp, în funcție de cerința problemei, căci paralelizăm procesarea variabilelor.
Operatori
Limbajul C oferă următoarele operații la nivel de bit:
- x & y (ȘI): bitul al k-lea are valoarea 1 dacă ambii biți k din x și y au valoarea 1;
- x | y (SAU): bitul al k-lea are valoarea 1 dacă cel puțin un bit k din x și y are valoarea 1;
- x ^ y (XOR sau SAU EXCLUSIV): bitul al k-lea are valoarea 1 dacă exact un bit k din x și y are valoarea 1;
- ~x (NOT): bitul al k-lea are valoarea 1 dacă bitul k din x are valoarea 0;
- x >> k (SHIFT DREAPTA): deplasează numărul în baza 2 cu k biți spre dreapta, pierzând ultimii k biți și completând cu k zerouri la stânga;
- x << k (SHIFT STÂNGA): deplasează numărul în baza 2 cu k biți spre stânga, pierzând primii k biți și completând cu k zerouri la dreapta;
Fie x = 18110 = 101101012 și y = 22710 = 111000112. Ambele pot fi reprezentate pe un singur octet fără semn.
| expresie | baza 2 | baza 10 |
|---|---|---|
| x | 10110101 | 181 |
| y | 11100011 | 227 |
| x & y | 10100001 | 161 |
| y | 11110111 | 247 |
| x ^ y | 01010110 | 86 |
| ~x | 01001010 | 74 |
| ~y | 00011100 | 28 |
| x >> 3 | 00010110 | 22 |
| x << 3 | 10101000 | 168 |
Observații:
- Remarcați diferența față de operatorii logici && (și), || (sau) și ! (not). De exemplu, operatorul && returnează 1 dacă ambii operanzi sunt non-zero, 0 altfel.
- Pe numere întregi, x >> k este totuna cu x / 2k, dar shiftarea este mult mai rapidă decât împărțirea.
- Pentru operatorul de negație (~), aveți grijă la mărimea tipului declarat, altfel vă veți trezi cu o mulțime de biți 1 nedoriți:
unsigned char x = 181;
printf("%hhu\n", ~x); // Tipărește 74
printf("%d\n", ~x); // Tipărește -182
printf("%u\n", ~x); // Tipărește 4294967114
Măști
O mască este un număr folosit pentru a face operații pe biți pe alt număr. De exemplu, pentru a afla rapid restul la împărțirea prin 8 a unui număr putem scrie:
int rest = x & 7;
În acest caz masca este 710 = 1112, iar x & 7 constă din ultimii 3 biți ai lui x.
Alte exemple de măști:
| scop | cod | observații |
|---|---|---|
| test de (im)paritate | x & 1 |
Acest test este mult mai rapid decât x % 2. |
| test dacă al k-lea bit al lui x este 1 | x & (1 << k) |
Acest test nu returnează 0 sau 1, ci 0 sau 2k. |
| setarea bitului k pe 1 | x |= (1 << k) |
|
| setarea bitului k pe 0 | x &= ~(1 << k) |
|
| inversarea valorii bitului k | x ^= ~(1 << k) |
Aplicație: Compactarea variabilelor
Dacă avem de stocat un vector cu un milion de elemente booleene, atunci fiecare element necesită, la limită, un singur bit. Deci putem folosi doar 128 KB în loc de 1 MB. Nu-i de colo!
Conceptual, dorim să înlocuim operatorii v[i] = x (pentru atribuire) și v[i] (pentru citire) cu două funcții set(i, x) și get(i). Astfel izolăm nivelul abstract de stocare a variabilelor, iar restul programului rămâne (aproape) nemodificat și ușor de înțeles.
Vom folosi reprezentarea:
| octetul 0 | octetul 1 | octetul 2 | |||||||||||||||||||||
| bitul 0 | bitul 1 | bitul 2 | bitul 3 | bitul 4 | bitul 5 | bitul 6 | bitul 7 | bitul 8 | bitul 9 | bitul 10 | bitul 11 | bitul 12 | bitul 13 | bitul 14 | bitul 15 | bitul 16 | bitul 17 | bitul 18 | bitul 19 | bitul 20 | bitul 21 | bitul 22 | bitul 23 |
Atunci bitul k va fi stocat pe octetul k / 8 (sau, echivalent, k >> 3), pe poziția k % 8 (sau, echivalent, k && 7). Notă: Poziția 0 este bitul cel mai puțin semnificativ, iar poziția 7 este bitul cel mai semnificativ. În imaginea de mai sus, biții sunt reprezentați invers decât în scrierea curentă.
Codul este:
void set(int i, int x) {
char mask = ~(1 << (i & 7));
b[i >> 3] = (b[i >> 3] & mask) ^ (x << (i & 7));
}
int get(int i) {
return (b[i >> 3] >> (i & 7)) & 1;
}
Funcția set() șterge întâi bitul deja existent la poziția i, folosind masca 11...101...11, care are 0 pe poziția dorită și 1 în rest. Apoi, atribuie noua valoare. Funcția get() izolează bitul dorit.
Aceste funcții merg cam cu 20% mai lent decât implementarea normală, cu vectori, un preț modest pentru o economie de memorie de 87%.
Stocarea pe 64 de biți
Putem implementa aceleași operații pe 64 de biți: în loc să împachetăm opt variabile booleene pe un octet (tipul char) putem împacheta 64 de variabile booleene pe tipul unsigned long long. Cu această reprezentare, impactul asupra vitezei este sub 10%. În special operațiile de reuniune și intersecție merg mult mai rapid, căci procesăm câte 64 de elemente simultan.
Atenție, însă, la detaliile de implementare:
- Dacă dimensionați vectorul doar ca
unsigned long long b[N / 64];, riscați să pierdeți un ultim element dacă N nu este multiplu de 64. Acest risc există, desigur, și pentru lucrul pe char, dar poate trece neobservat deoarece, în general, datele de intrare sunt multiplu de 8. - Unele valori trebuie convertite explicit la unsigned long long.
Codul rezultat este:
typedef unsigned long long u64;
void set(int i, int x) {
u64 mask = ~(1ull << (i & 63));
b[i >> 6] = (b[i >> 6] & mask) ^ ((u64)x << (i & 63));
}
int get(int i) {
return (b[i >> 6] >> (i & 63)) & 1;
}
Stocarea valorilor pe doi sau patru biți
Ce alte valori interesante mai pot fi compactate într-un octet?
- numerele pe 2 biți, cu valori între 0 și 3 (de exemplu: codificarea direcțiilor NSEV într-o matrice)
- numerele pe 4 biți, cu valori între 0 și 15 (de exemplu: codificarea a două cifre zecimale într-un singur octet; valorile hexa A-F rămân neutilizate)
Valorile acestea pot fi compactate câte 4 (respectiv 2) pe un octet sau câte 32 (respectiv 16) pe un unsigned long long. Implementarea vă rămâne vouă ca temă.
Aplicație: Calculul unor proprietăți ale numerelor pe 32 / 64 de biți
Uneori veți avea nevoie să calculați proprietăți ca
- numărul de biți 1 din reprezentarea binară a lui x (popcount);
- logaritmul în baza 2 al lui x (care este totuna cu numărul de ordine al celui mai din stânga bit 1);
- dacă x este putere al lui 2.
Este bine să știți că există metode și metode de a face aceste calcule, din care unele pot fi de 10-20 de ori mai rapide decât celelalte. Dacă aceste calcule sunt o componentă critică a programului vostru, este bine să știți ce merge și ce nu merge. Experimentați din timp.
Includ ca exemplu Media:popcount.cpp, unde am experimentat cu 5 metode de a calcula popcount. Timpii obținuți pentru 100.000.000 de evaluări sunt:
| metoda | timp (ms) | scurtă descriere |
|---|---|---|
| naiv | 5.000 | shiftează câte un bit și vede dacă este 1 |
| Kernighan | 3.265 | folosește observația că x & (x - 1) șterge ultimul bit de 1
|
| lookup table 1 | 355 | precalculează un tabel pentru numerele 0-255 și sparge întregul în octeți |
| lookup table 2 | 460 | idem |
| în paralel | 270 | calculează răspunsul pentru bucăți de 2, 4, 8, 16, 32, 64 de biți în paralel |
Se vede că există diferențe notabile între ultimele trei metode, dar oricare dintre ele mătură pe jos cu metodele naive.
Probleme
Lectură suplimentară
- Low Level Bit Hacks You Absolutely Must Know (nivel mediu)
- Bit Twiddling Hacks (nivel avansat)
Codificări
Un concept general care intervine uneori în programare este codificarea unui set de n obiecte cu numere între 0 și n - 1.
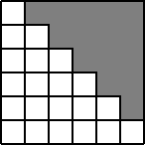
Să ne închipuim o problemă în care avem nevoie doar de jumătatea inferioară a unei matrice pătrate. Un caz comun este când matricea este simetrică sau antisimetrică și este o risipă să o stocăm în întregime. Să presupunem că avem nevoie și de diagonala principală. Cazul în care nu avem nevoie de diagonală și cazul în care avem nevoie de triunghiul superior sunt tratate similar.
Trei reprezentări care ne sunt la îndemână sunt:
- folosim o matrice normală -- pur și simplu ignorăm jumătate din ea, irosind jumătate din spațiu;
- folosim un vector de vectori alocați dinamic;
- un vector alocat static, către care ținem pointeri la vectori tot mai lungi (liniile).
Din a treia reprezentare derivăm o soluție bazată pe codificare, din care vom deduce patru operații generale.
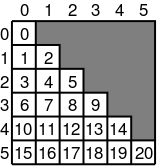
Începem prin a număra pătratele folosite efectiv. Desigur, acestea vor fi . Apoi le numerotăm într-o manieră convenabilă, începând de la 0, de exemplu de la stânga la dreapta și de sus în jos.
Pentru stocarea matricei vom folosi un vector de elemente, ceea ce este optim. Trebuie să implementăm două operații:
- codificare: dându-se coordonatele i și j în matrice, ce indice s le corespunde în vector?
- decodificare: dându-se un indice s în vector, ce coordonate i și j le corespunde în matrice?
Codificarea se poate implementa ușor în O(1). Observăm că numerele de pe prima coloană sunt triunghiulare, așadar:
int codifica(int i, int j) {
return i * (i + 1) / 2 + j;
}
Decodificarea poate să nu fie necesară, în funcție de natura problemei. O primă soluție, în timp , este să căutăm binar linia i pe care apare indicele s:
void decodifica(int s, int *i, int *j) {
*i = cautaBinar(s); // Caută binar cel mai mare i pentru care i * (i + 1) / 2 ≤ s
*j = s - *i * (*i + 1) / 2;
}
Eventual, numerele triunghiulare pot fi precalculate într-un vector, pentru a evita înmulțirile. Menționăm în treacăt și o decodificare în în locul căutării binare. Rezolvăm o ecuație de gradul 2 în i:
Constanta acestei decodificări este mare, căci face operații pe numere reale.
În situații generale ne mai sunt utile două operații:
- incrementare: dându-se un obiect, să se calculeze următorul;
- decrementare: dându-se un obiect, să se calculeze anteriorul.
Pentru problema sus-menționată, operațiile sunt ușor triviale:
void incrementeaza(int *i, int *j) {
// Nu facem verificări de limite
if (*j == *i) {
(*i)++;
*j = 0;
} else {
(*j)++;
}
}
void decrementeaza(int *i, int *j) {
if (*j == 0) {
(*i)--;
*j = *i;
} else {
(*j)--;
}
}
Codificarea permutărilor
Să considerăm toate permutările mulțimii { 1, ..., n } ordonate lexicografic. Se dau n, una dintre permutări și un număr k. Care este a k-a permutare după cea dată?
Pentru k mic, putem aplica de k ori operația de incrementare, care o generează dintr-o permutare pe cea următoare. Pentru k mare, este mai eficient să codificăm permutarea dată printr-un număr, să adunăm k la acel număr și să decodificăm indicele rezultat. Să ne gândim cum ar putea fi implementate aceste trei operații (operația de decrementare va fi foarte similară cu cea de incrementare).
Codificare
Fie permutarea (3 7 2 1 4 6 5). Știm că există permutări care încep cu 1 sau cu 2. Deci ținem minte și ne întrebăm: dintre toate permutările mulțimii { 1, 2, 4, 5, 6, 7 }, a câta este (7 2 1 6 4 5)? Aceasta nu este o permutare, căci lipsește 3 din ea, dar o putem transforma într-o permutare scăzând 1 din valorile mai mari decât 3: (6 2 1 3 5 4). Rezolvăm noua problemă într-o manieră similară. Tabelul următor sumarizează procesul.
| permutare | permutări care încep cu un element mai mic | se reduce la |
|---|---|---|
| (3 7 2 1 4 6 5) | (6 2 1 3 5 4) | |
| (6 2 1 3 5 4) | (2 1 3 5 4) | |
| (2 1 3 5 4) | (1 2 4 3) | |
| (1 2 4 3) | (1 3 2) | |
| (1 3 2) | (2 1) | |
| (2 1) | (1) | |
| total |
Complexitatea algoritmului naiv este :
codifică(p, n) {
total = 0;
for (i = 0; i < n - 1; i++) {
total += (p[i] - 1) * (n - 1 - i)!;
for (j = i + 1; j < n - 1; j++) {
if (p[j] > p[i]) {
p[j]--;
}
}
}
return total;
}
Putem reduce complexitatea la . Observăm că, la pasul i, dorim în fapt să aflăm câte elemente mai mici decât p[i] nu am văzut încă. Echivalent, știind că înainte de i există i - 1 numere, dorim să știm pe câte dintre acestea le-am văzut deja. Putem face aceasta cu un arbore indexat binar (AIB):
codifică(p, n) {
initAIB(0); // pune 0 peste tot în vectorul reprezentat de AIB
total = 0;
for (i = 0; i < n - 1; i++) {
total += (p[i] - 1 - sumaAIB(1, p[i])) * (n - 1 - i)!;
incrementeazăAIB(p[i]);
}
return total;
}
Decodificare
Cum era de așteptat, decodificarea urmează aceiași pași, în ordine inversă. Să spunem că n = 7 și primim codul 2065. Care este prima cifră a permutării? În mod sigur este , deoarece există permutări care încep cu 1 și 2. Codul rămas este și mai avem de plasat cifrele 1, 2, 4, 5, 6, 7.
Care este următoarea cifră a permutării, ținând cont că pe 3 l-am văzut deja? Deoarece , ne trebuie a 6-a cifră pe care nu am scris-o deja, adică 7. Și așa mai departe.
Din nou, implementarea naivă este , dar o putem reduce la folosind un AIB. Folosim AIB-ul ca să răspundem la întrebarea „care este a k-a cea mai mică cifră pe care nu am scris-o deja?”.
decodifică(n, cod, p) {
initAIB(1); // pune 1 peste tot în vectorul reprezentat de AIB
for (i = 0; i < n - 1; i++) {
p[i] = cautăDupăFrecvență(1 + cod / (n - 1 - i)!); // caută binar cel mai mic indice în AIB pentru care frecvența este
cod %= (n - 1 - i)!;
decrementeazăAIB(p[i]);
}
}
Incrementare
Fie permutarea (3 1 5 7 6 4 2). Care este următoarea în ordine lexicografică?
Să ne prefacem că suntem somnambuli și, în somn, scriem toate aceste permutări. Brusc, ne trezim și ne dăm seama că am ajuns la (3 1 5 7 6 4 2). Ce deducem de aici? De exemplu, deducem că suntem în curs de enumerare a permutărilor care încep cu (3 1 5 7). Dar, dintre acestea, (3 1 5 7 6 4 2) este cea mai mare lexicografic, deoarece sufixul (6 4 2) este ordonat descrescător. De asemenea, deducem că suntem în curs de enumerare a permutărilor care încep cu (3 1 5). La fel, dintre acestea, (3 1 5 7 6 4 2) este cea mai mare lexicografic, deoarece sufixul (7 6 4 2) este ordonat descrescător. Mergând încă un pas mai sus, deducem că suntem în curs de enumerare a permutărilor care încep cu (3 1). Cum pe cele cu (3 1 5) le-am terminat, trecem la următoarele, adică cele cu (3 1 6). Dintre acestea, cea mai mică este (3 1 6 2 4 5 7).
Cum ajungem de la (3 1 5 7 6 4 2) la (3 1 6 2 4 5 7)?
- Găsim cel mai din dreapta punct nedescrescător din permutare: (3 1 5 7 6 4 2).
- Găsim cel mai mic element din dreapta lui 5 care să fie mai mare decât 5: (3 1 5 7 6 4 2).
- Inversăm elementele 5 și 6 între ele: (3 1 6 7 5 4 2). Astfel arătăm că am trecut la enumerarea permutărilor cu (3 1 6).
- Sortăm crescător bucata din vector de după 6. Cum prin definiție ea era descrescătoare, trebuie doar să o răsturnăm: (3 1 6 2 4 5 7).
Algoritmul are complexitate
incrementează(n, p) {
int i = n - 2;
while (i >= 0 && p[i] > p[i + 1]) {
i--;
}
if (i < 0) {
// Caz special: permutarea este ultima dpdv lexicografic
}
j = indicele maxim pentru care j > i și p[j] > p[i]
schimbă p[i] cu p[j]
răstoarnă bucata din vector p[i + 1 ... n - 1]
}
Alte codificări
În limita timpului disponibil.
Combinări
- codificare: dându-se n și k, ne imaginăm combinările enumerate lexicografic. Dându-se o combinare, care este indicele ei?
- decodificare: problema inversă
- incrementare: care este combinarea următoare celei date?
Aranjamente
Aceleași 3 întrebări pentru aranjamente (combinări permutate).
Codul Gray
Vezi Codul Gray.
Mulțimea submulțimilor
Să ne închipuim cele submulțimi nevide ale mulțimii { 1, ..., n}, ordonate alfabetic. Pentru n = 3 vom avea:
{ 1 }
{ 1, 2 }
{ 1, 2, 3 }
{ 1, 3 }
{ 2 }
{ 2, 3 }
{ 3 }
Să se implementeze operațiile de codificare, decodificare și incrementare.
Probleme
- Suma4 (OJI 2011)