Optional numere mari
Lecţie
Numere mari
Unele probleme necesită lucrul cu numere mai mari decît ne permite tipul long long (cu aproximație 18 cifre zecimale, mai exact 264). Ce facem în acest caz? Stocăm aceste numere în vectori, cîte o cifră în fiecare element al vectorului. În continuare voi prezenta cîteva probleme clasice cu astfel de numere.
Reprezentare
Numerele mari se reprezintă într-un vector, ultima lor cifra pe prima poziție a vectorului, penultima pe a doua poziție, și așa mai departe, precum se vede în figură.
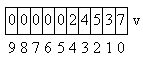
Observați că am reprezentat vectorul invers, de la dreapta la stînga, pentru ușurința citirii numărului.
Observăm că vectorul v are ca elemente cifre, adică întregi cuprinși între 0 și 9. Pentru a folosi cît mai puțină memorie vom folosi cel mai mic întreg existent în limbajul C și anume tipul caracter. Să nu uităm că tipul caracter poate fi văzut atît ca și caracter cît și ca un întreg pe opt biți, cuprins între -128 și 127. A
char v[100];
De asemenea, pentru un număr mare trebuie să ținem minte și numărul său de cifre. În exemplul nostru acesta este 5. Ca ultimă mențiune, trebuie să avem grijă ca cifrele nefolosite din vector să fie zero. Acest lucru este foarte important atunci cînd numărul poate să crească, cum ar fi la adunare, sau înmulțire.
Adunarea unui număr mic la unul mare
Fie v un număr mare cu n cifre. Dorim să adunăm la el un număr "mic", a. Pentru aceasta vom proceda similar cu procedura de adunare "de mînă": vom aduna a la prima cifră a numărului, vom stoca pe prima poziție ultima cifră a acestui număr, apoi vom calcula transportul prin împărțire la zece. Acest transport se adună la a doua cifră, stocînd ultima cifră a rezultatului pe a doua poziție și calculînd noul transport prin împărțire la zece. Diferența față de adunarea "de mînă" este că transportul poate fi mai mare decît 9. Iată secvența de cod care adună numărul mare (n, v) cu numărul a:
i = 0;
while ( a > 0 ) {
a += v[i];
v[i] = a % 10;
a /= 10;
i++;
}
if ( i > n )
n = i;Scăderea unui număr mic din unul mare
Scăderea unui număr mic din unul mare este similară cu adunarea. Transportul va fi negativ. Trebuie însă să fim atenți la un lucru: operația % (modulo) în C nu se comportă ca la matematică. La matematică restul împărțirii a două numere este pozitiv sau zero. În C restul împărțirii unui număr negativ la unul pozitiv este negativ sau zero. De aceea codul trebuie modificat față de adunare pentru a calcula restul pozitiv al împărțirii la zece. De asemenea trebuie să avem grijă să scădem numărul de cifre, dacă este cazul. Vom păstra în nn poziția ultimei cifre diferite de zero. Iată secvența de cod care scade numărul mic a din numărul mare (n, v):
a = -a;
nn = i = 0;
while ( a < 0 ) {
a += v[i];
v[i] = a % 10;
a /= 10;
if ( v[i] < 0 ) {
v[i] += 10;
a--;
nn = i;
}
i++;
}
if ( i >= n )
n = nn + 1;Atenție: programul de mai sus presupune că numărul mic este mai mic sau egal cu numărul mare.
Adunarea a două numere mari
Adunarea a două numere mari este similară cu adunarea unui număr mare cu unul mic. Vom folosi un transport și vom aduna cifră cu cifră cele două numere mari. În final vom testa dacă mai avem transport. Dacă avem el este maxim o cifră (demonstrați). Iată secvența de cod care adună numărul mare (n2, v2) la (n1, v1) depunînd rezultatul tot în (n1, v1):
n1 = n1 < n2 ? n2 : n1;
t = 0;
for ( i = 0; i < n1; i++ ) {
t = t + v1[i] + v2[i];
v1[i] = t % 10;
t /= 10;
}
if ( t > 0 ) {
v1[i] = t;
n1++;
}Scăderea a două numere mari
Scăderea a două numere mari este similară cu scăderea unui număr mare din unul mic. Vom folosi un transport negativ și vom scădea cifră cu cifră cele două numere mari. După ce se termină cifrele numărului de scăzut vom continua scăderea pînă ce transportul devine zero. Ca și la scăderea unui număr mic va trebui să avem grijă să scădem numărul de cifre dacă este cazul. Iată secvența de cod care scade numărul mare (n2, v2) din numărul mare (n1, v1):
nn = t = i = 0;
while ( i < n2 || t < 0 ) {
t = t + v1[i] - v2[i];
v1[i] = t % 10;
t /= 10;
if ( v1[i] < 0 ) {
v1[i] += 10;
t--;
nn = i;
}
i++;
}
if ( i >= n1 )
return n1 = nn + 1;Atenție: programul de mai sus presupune că numărul (n2, v2) este mai mic sau egal cu numărul (n1, v1).
Înmulțirea unui număr mare cu unul mic
Înmulțirea unui număr mare cu unul mic este similară cu adunarea unui număr mare cu unul mic. Vom folosi un transport la care adunăm cifra curentă înmulțită cu numărul mic. Ultima cifră a transportului se stochează în cifra curentă, iar transportul se împarte la zece, apoi trecem la cifra următoare. După ce se termină cifrele numărului mare vom continua procedura pînă ce transportul devine zero. Trebuie să avem grijă să actualizăm numărul de cifre dacă este cazul. Iată secvența de cod care înmulțește numărul mic a cu numărul mare (n, v):
t = i = 0;
while ( i < n || t > 0 ) {
t = t + a * v[i];
v[i] = t % 10;
t /= 10;
i++;
}
if ( i > n )
n = i;I