Rucsac
Note de curs Clasa a 11-a , Dinamica, Isabela Coman
Problema Rucsacului
Considerăm un set de n obiecte, fiecare fiind caracterizat de un volum ( dimensiune ) vol și de o valoare val, și un rucsac cu un volum G. Să se selecteze un subset de obiecte astfel încât volumul total al obiectelor selectate să fie <= G iar valoarea totală a obiectelor selectate să fie maximă. Variante:
- Varianta continuă (fracționară): pot fi selectate obiecte in întregime sau fracțiuni ale obiectelor.
- Varianta discretă(0-1): obiectele pot fi selectate doar în întregime
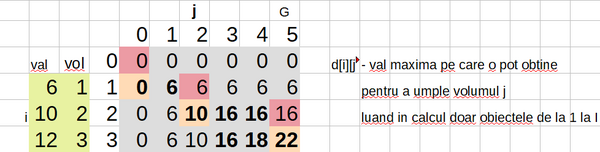
Exemplu: n = 3, G = 5, vol 1 2 3 val 6 10 12 unit 6 5 4
Pentru Varianta Fractionara Tehnica Greedy ne poate da solutia problemei:
- Se sortează lista de obiecte descrescător după valoarea pe unitatea de volum unit = val / dim
- Se selectează obiectele în această ordine până când nu mai încap elemente in rucsac. Daca am obtinut un volum egal cu volumul Ruxacului, atunci am obtinut solutia finala. Altfel, vom lua din urmatorul obiect o fractiune, pentru a completa volumul Ruxacului.
Astfel, pentru exemplul de mai sus, pentru a umple ruscacul de dimensiune 5, vom selecta primele 2 obiecte si 2 unitati din obiectul al treilea, de volum 3. solutia va fi: ( 1, 1, 2/3 ) - obtinem valoarea: 6 + 10 + 8 = 24
Pentru Varianta discreta Tehnica Greedy nu ne va da solutia optima. Conform acestei tehnici, vom pune in rucsac primele 2 obiecte, obtinand solutia:
- solutia ( 1, 1, 0 ) Alegem primele 2 obiecte care ocupa un volum = 3 si obtinem o valoare de: 6 + 10 = 16
O solutie mai buna ar fi:
- solutia (0, 1, 1 ) - Alegem ultimele 2 obiecte care ocupa un volum = 5 si obtinem o valoare de: 10 + 12 = 22
Problema Rucsacului - Varianta discretă(0-1)
Problema rucsacului poate fi reformulată astfel: se caută (s1,s2,…,sn) cu si in {0,1} astfel încât:
* s1*d1 +…+ sn*dn <= C (restricție) * s1*v1 +…+ sn*vn este maximă (criteriu de optim)
Vectorul s descrie ce elemente sunt selectate, astfel incat valoarea lor sa fie maxima, <= C
Varianta iterativa - bottom up
#include <iostream>
#include <fstream>
using namespace std;
const int NMAX = 1000; // nr maxim de obiecte
const int GMAX = 10000;
int a[NMAX+1][GMAX+1];
int n, G, g; // nr obiectelor, capacitatea rucsacului
int vol[NMAX+1], val[NMAX+1];
int main() {
cin >> n >> G;
for( int i = 1; i <= n; i++ )
cin >> vol[i] >> val[i];
for( int i = 1; i <= n; i++ )
for( int j = 1; j <= G; j++ ) {
if ( j < vol[i] )
a[i][j] = a[i-1][j];
else
a[i][j] = max ( a[i-1][j], a[i-1][j-vol[i]] + val[i] );
}
for( int i = 0; i <= n; i++ ){
for( int j = 0; j <= G; j++ )
cout << a[i][j] << " ";
cout << '\n';
}
cout << a[n][G] << '\n'; // val maxima obtinua
//ce obiecte am selectat?
int sol[NMAX+1] = {0};
int i = n;
int j = G;
while ( j ){
if ( a[i][j] != a[i-1][j] ) {
sol[i] = 1; // elem i e selectat
j = j - vol[i]; // ne ducem pe col volumului ramas
}
i --;
}
for( int i = 1; i <= n; i++ )
if (sol[i])
cout << i << " ";
return 0;
}
/*
3 5
1 6
2 10
3 12
*/Varianta recursiva top-down + Memoizare
Pt a construi soluția sunt suficiente doar valorile marcate. Numărul calculelor poate fi redus dacă se calculează doar valorile necesare construcției solutiei. Acest lucru se poate realiza prin îmbinarea abordării descendente cu cea ascendentă (cu reținerea valorilor calculate). Aceasta este denumita tehnica memoizării.
- Abordarea ascendentă clasică (prezentata anterior )rezolvă toate subproblemele (chiar și cele care nu contribuie la soluția optimă) însă fiecare problemă este rezolvată o singură dată.
- Abordarea descendentă ( recursiva ) clasică rezolvă doar subproblemele ce contribuie la soluția problemei însă o subproblemă este rezolvată de câte ori apare (din acest motiv implementarea recursivă este în general ineficientă)
Tehnica memoizării rezolvă o singură dată doar subproblemele ce contribuie la soluția problemei
Etape:
- Se inițializează matrice cu o valoare diferita de orice valoare s-ar obține prin dezvoltarea relației de recurență, pentru a marca faptul ca o valorile nu sunt inca calculate.
- Se calculează valoarea țintă a[n,G] în manieră recursivă însă toate valorile intermediare se stochează și se utilizează atunci când e necesar.
#include <iostream>
#include <fstream>
#define D 0
using namespace std;
const int NMAX = 1000; // nr maxim de obiecte
const int GMAX = 10000;
int a[NMAX+1][GMAX+1];
int n, G, g; // nr obiectelor, capacitatea rucsacului
int vol[NMAX+1], val[NMAX+1];
int comp ( int i, int j ){
if ( i == 0 || j == 0 ) {
return 0;
}
if ( a[i][j] != -1 ) // daca val e deja calculata, o returnam
return a[i][j];
int x = comp( i-1, j ); // daca nu as avea comp i-1 in sol
if ( j < vol[i] )
a[i][j] = x;
else
a[i][j] = max ( x, comp( i-1, j-vol[i]) + val[i] );
return a[i][j];
}
int main() {
cin >> n >> G;
for( int i = 1; i <= n; i++ )
cin >> vol[i] >> val[i];
for( int i = 1; i <= n; i++ )
for( int j = 1; j <= G; j++ ) {
a[i][j] = -1;
}
cout << comp(n,G) << '\n';
if ( D ){
for( int i = 0; i <= n; i++ ){
for( int j = 0; j <= G; j++ )
cout << a[i][j] << " ";
cout << '\n';
}
}
//ce obiecte am selectat?
int sol[NMAX+1] = {0};
int i = n;
int j = G;
while ( j ){
if ( a[i][j] != a[i-1][j] ) {
sol[i] = 1; // elem i e selectat
j = j - vol[i]; // ne ducem pe col volumului ramas
}
i --;
}
for( int i = 0; i <= n; i++ )
if (sol[i])
cout << i << " ";
return 0;
}
/*
3 5
1 6
2 10
3 12
*/Optimizarea memoriei utilizate in varianta iterativa Bottom-up
In solutia iterativa, putem observa ca pentru o anumita linie din dinamica, recurenta nu se foloseste decat de linia precedenta, deci retinerea intregului tablou este inutila, in cazul in care trebuie sa calculam doar valoarea maxima a rucsacului. Putem sa reţinem doar o singura linie, dacă parcurgem linia în sensul invers al greutăţilor. rucsac varena
#include <iostream>
#include <fstream>
#define D 0
using namespace std;
const int NMAX = 5000; // nr maxim de obiecte
const int GMAX = 10000;
ifstream fin("rucsac.in");
ofstream fout("rucsac.out");
int a[GMAX+1];
int n, G, g; // nr obiectelor, capacitatea rucsacului
int vol[NMAX+1], val[NMAX+1];
int main() {
fin >> n >> G;
for( int i = 1; i <= n; i++ )
fin >> vol[i] >> val[i];
for( int i = 1; i <= n; i++ ) {
for( int j = G; j >= vol[i]; j-- ) {
a[j] = max ( a[j], a[j-vol[i]] + val[i] );
}
if ( D ) {
for( int j = 1; j <= G; j++ )
cout << a[j] << " ";
cout << '\n';
}
}
fout << a[G] << '\n'; // val maxima obtinua
return 0;
}Aplicatii
Se citesc doua numere naturale N si K si un sir v de N numere naturale. Sa se raspunda la urmatoarea intrebare: Cate subsiruri ale sirului initial au suma elementelor egala cu K?
#include <iostream>
#include <fstream>
#define MOD 999979
using namespace std;
const int NMAX = 500; // nr maxim de obiecte
const int GMAX = 250000;
ifstream fin("rucsac.in");
ofstream fout("rucsac.out");
int a[GMAX+1];
int vol;
int n, G; // nr obiectelor, capacitatea rucsacului
int main() {
fin >> n >> G;
a[0] = 1;
for( int i = 1; i <= n; i++ ) {
fin >> vol;
for( int j = G; j >= vol; j-- )
if (a[j-vol]) {
a[j] += a[j-vol];
a[j] %= MOD;
}
}
fout << a[G] << '\n'; // val maxima obtinua
return 0;
}Sabin merge la colindat de Halloween. Ştiind ca poate colinda la n case, iar la fiecare primeşte g[1], g[2], ..., g[n] bomboane, iar în rucsacul lui încap G bomboane, aflaţi numărul minim de case pe care trebuie să le colinde Sabin pentru a umple ghiozdanul. Daca nu poate umple ghiozdanul, se afiseaza mesajul "NU".
Solutie O(n) memorie
#include <iostream>
#include <fstream>
using namespace std;
const int NMAX = 1000; // nr maxim de obiecte
const int GMAX = 10000;
int g[NMAX + 1]; // cantitatile de bomboane
int a[GMAX + 1];
int n, G; // nr obiectelor, capacitatea rucsacului
int main() {
cin >> n >> G;
for( int i = 1; i <= n; i++ )
cin >> g[i];
for( int i = 1; i <= G; i++ )
a[i] = NMAX + 1;
for( int i = 1; i <= n; i++ )
for( int j = G; j >= g[i]; j-- ) {
if( a[j] > a[j - g[i]] + 1 )
a[j] = a[j - g[i]] + 1;
}
if( a[G] == NMAX + 1 )
cout << "NU";
else
cout << a[G];
return 0;
}Tema
Varena
Infoarena