Note de curs, clasele 9-10, 27 martie 2014

From Algopedia
Jump to navigationJump to search

Flood fill

Se dă o matrice de numere întregi unde unele valori (să zicem 0) semnifică spații goale, iar altele (să zicem 1) semnifică pereți sau obstacole. Algoritmul fill oferă o modalitate de a vizita toate spațiile goale accesibile dintr-un punct de pornire dat. În funcție de problemă, vecinătatea a două puncte se definește pe 4 direcții sau pe 8 (în această lecție, pentru brevitate, vom trata vecinătatea pe 4 direcții).

Această lecție se bazează pe lecția de la clasele 7-8.

Varianta de bază

O implementare recursivă scurtă și clară este: 

void fill(int l, int c) {
  if (l >= 0 && l < m && c >= 0 && c < n && a[l][c] == 0) {
    a[l][c] = 1; // marchează punctul (l, c) ca vizitat
    // ... eventual și alte procesări pentru acest punct

    fill(l - 1, c);
    fill(l, c + 1);
    fill(l + 1, c);
    fill(l, c - 1);
  }
}

Această variantă are două dezavantaje:

  1. Este lentă. De câte ori este vizitat punctul (l, c)? De atâtea ori câți vecini accesibili are, căci fiecare dintre acești vecini va apela exact o dată fill(l, c).
  2. Folosește multă memorie. Stiva utilizată de recursivitate poate ajunge la O(mn), după cum se vede în imaginea de mai jos.



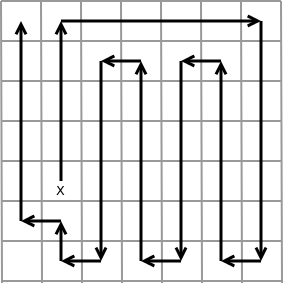
Pornind de la punctul (4, 1) și presupunând că apelăm cei patru vecini în ordinea N-E-S-V, stiva va conține aproape toate punctele matricei. Aceasta se întâmplă indiferent de punctul de pornire și de ordinea vizitării vecinilor.

Bordarea matricei

Dacă bordăm matricea cu obstacole (valori 1), eliminăm patru din cele cinci condiții testate. De aici înainte, vom presupune că matricea este bordată și vom elimina condițiile de încadrare în limite.

Testarea înainte de reapelare

Putem testa dacă un vecin merită vizitat înainte de a face apelul recursiv. 

void fill(int l, int c) {
  a[l][c] = 1; // marchează punctul (l, c) ca vizitat
  // ... eventual și alte procesări pentru acest punct

  if (a[l - 1][c] == 0) {
    fill(l - 1, c);
  }
  if (a[l][c + 1] == 0) {
    fill(l, c + 1);
  }
  if (a[l + 1][c] == 0) {
    fill(l + 1, c);
  }
  if (a[l][c - 1] == 0) {
    fill(l, c - 1);
  }
}

Codul se complică un pic, dar acum elementul (l, c) va fi vizitat o singură dată. Primul lucru pe care îl face rutina este să marcheze punctul ca vizitat, ceea ce previne vizitele ulterioare.

Nu știu dacă devine mult mai rapid. Poate cineva dintre voi să testeze?

Reducerea memoriei prin folosirea de variabile globale

Prima regulă atunci când ne temem că recursivitatea poate avea prea multe niveluri este să reducem memoria folosită per nivel. Putem elimina toate argumentele funcției fill() printr-un artificiu urât, dar eficient. Declarăm variabilele l și c globale și le gestionăm noi înșine: 

int l, c;

void fill() {
  if (a[l][c] != 0) {
    return;
  }
  a[l][c] = 1;
  l--;
  fill();
  l++;
  c++;
  fill();
  c--;
  l++;
  fill();
  l--;
  c--;
  fill();
  c++;
}

Trebuie să avem grijă să modificăm variabilele l și c într-o manieră consecventă. Pentru a vă convinge că rutina funcționează, observați că, după fiecare 3 linii, variabilele l și c revin la valorile pe care le aveau la intrarea în funcție.

  • Aici ar merita inserată o discuție despre GOSUB în BASIC și despre cum poți să programezi structurat chiar atunci când limbajul nu te ajută (Sinclair BASIC nu avea instrucțiunea while).

Folosirea propriei stive

Putem folosi și propria stivă, asupra căreia avem ceva mai mult control decât asupra stivei compilatorului. Atunci algoritmul de fill devine iterativ. 

void fill(int l, int c) {
  a[l][c] = 1;
  s = stivă goală;
  push(s, l, c);
  while(s != stivă goală) {
    pop(s, &l, &c);

    if (a[l - 1][c] == 0) {
      a[l - 1][c] = 1;
      push(s, l - 1, c);
    }
    if (a[l][c + 1] == 0) {
      a[l][c + 1] = 1;
      push(s, l, c + 1);
    }
    if (a[l + 1][c] == 0) {
      a[l + 1][c] = 1;
      push(s, l + 1, c);
    }
    if (a[l][c - 1] == 0) {
      a[l][c - 1] = 1;
      push(s, l, c - 1);
    }
}

Flood fill cu linie de baleiere

Prezentăm în trecere o ultimă optimizare, cu mențiunea că este mai greu de implementat în timp de concurs. Pe de altă parte, algoritmul cu linie de baleiere este cu mult mai rapid, căci face mai puține apeluri recursive.

Algoritmul operează cu intervale orizontale (linii) definite prin triplete (l, c1, c2) cu semnificația „intervalul pe linia l între coloanele c1 și c2”. Algoritmul menține o stivă cu intervalele încă neevaluate. 

void fill(int l, int c) {
  s = stivă goală;
  push(s, l, c, c); // pornim cu un interval de un singur pixel
  while(s != stivă goală) {
    (l, c1, c2) = pop(s);
    extinde c1 către V;
    extinde c2 către E;
    setează pe 1 toate elementele de la (l, c1) la (l, c2);
    examinează liniile l - 1 și l + 1, între coloanele c1 și c2;
    pune pe stivă toate intervalele găsite;
  }
}

Puteți vedea acest algoritm în funcțiune (la viteză redusă) într-un vechi joc de ZX Spectrum, The Hobbit. Dacă vă întrebați de ce grafica este implementată așa, răspunsul este: pentru că e foarte economic. Când toată memoria disponibilă este 48 KB (inclusiv memoria video), fiecare octet contează. Cam de câți octeți este nevoie pentru a reprezenta una dintre imaginile pe care le vedeți?

Aplicații

Flood fill se folosește, în general, pentru probleme de conexitate în matrice întregi, cum ar fi:

  • numărarea „insulelor” între care nu se poate circula;
  • calculul ariei fiecărei insule.

Algoritmul lui Lee

Algoritmul lui Lee calculează ceva în plus față de algoritmul simplu de fill: distanțele minime de la punctul de pornire până la toate punctele vizitate. El derivă din parcurgerea în lățime a grafurilor (BFS), despre care am discutat în noiembrie. Ne imaginăm matricea ca pe un graf în care fiecare nod are (cel mult) patru vecini, cei de la N, S, E și V.

Dat fiind că graful nostru are o structură particulară, nu avem nevoie să-l reprezentăm ca pe un graf, iar algoritmul se simplifică considerabil.

Nu mai redăm codul pentru acest algoritm. El arată aproape identic cu flood fill cu stivă proprie, cu două diferențe:

  • Folosește o coadă în loc de stivă.
  • Menține o matrice în plus, a distanțelor. Când a[l][c] capătă valoarea 1, d[l][c] capătă valoarea predecesorului său +1.

Demonstrația de optimalitate a drumurilor prezentată la parcurgerea în lățime se aplică și la matrice.

Aplicații

Algoritmul lui Lee este necesar când dorim să aflăm informații despre drumuri și distanțe:

  • Găsirea ieșirii dintr-un labirint / castel / hartă.
  • Găsirea celui mai scurt drum între două puncte dintr-o matrice.
  • În lumea reală, proiectarea de circuite electronice

Probleme

  • Taxa (ONI 2013, clasa a 10-a)
  • Gheizere (ONI 2012, clasa a 10-a)
  • Tsunami (ONI 2011, clasa a 10-a)
  • Dreptunghiuri (ONI 2010, clasa a 10-a)
  • Ferma (OJI 2014, clasa a 10-a) -- nu este online, dar puteți descărca arhiva, inclusiv testele, de la infoarena
  • Zona (OJI 2013, clasa a 10-a)
  • AI (OJI 2011, clasa a 10-a)
  • Oraș (Varena)

Concluzie: clasa a 10-a să ia aminte. :-)

Referințe

Retrieved from "https://www.algopedia.ro/wiki/index.php?title=Note_de_curs,_clasele_9-10,_27_martie_2014&oldid=11460"